Luogu P5515 [MtOI2019]灵梦的计算器

简化题意

给定三个实数 \(n, a, b\)，求方程 \(\left \lfloor {x ^ a + x ^ b} \right \rfloor = \left \lfloor {n ^ a + n ^ b} \right \rfloor\) 的解的最大值与最小值的差。

题目分析

前置知识：导数，极限。

题意可化为：求方程

\[{x ^ a + x ^ b} = \left \lfloor {n ^ a + n ^ b} \right \rfloor
\]

\[{x ^ a + x ^ b} = \left \lfloor {n ^ a + n ^ b} \right \rfloor + 1
\]

方程解的差。

画出图像来大概是这样：

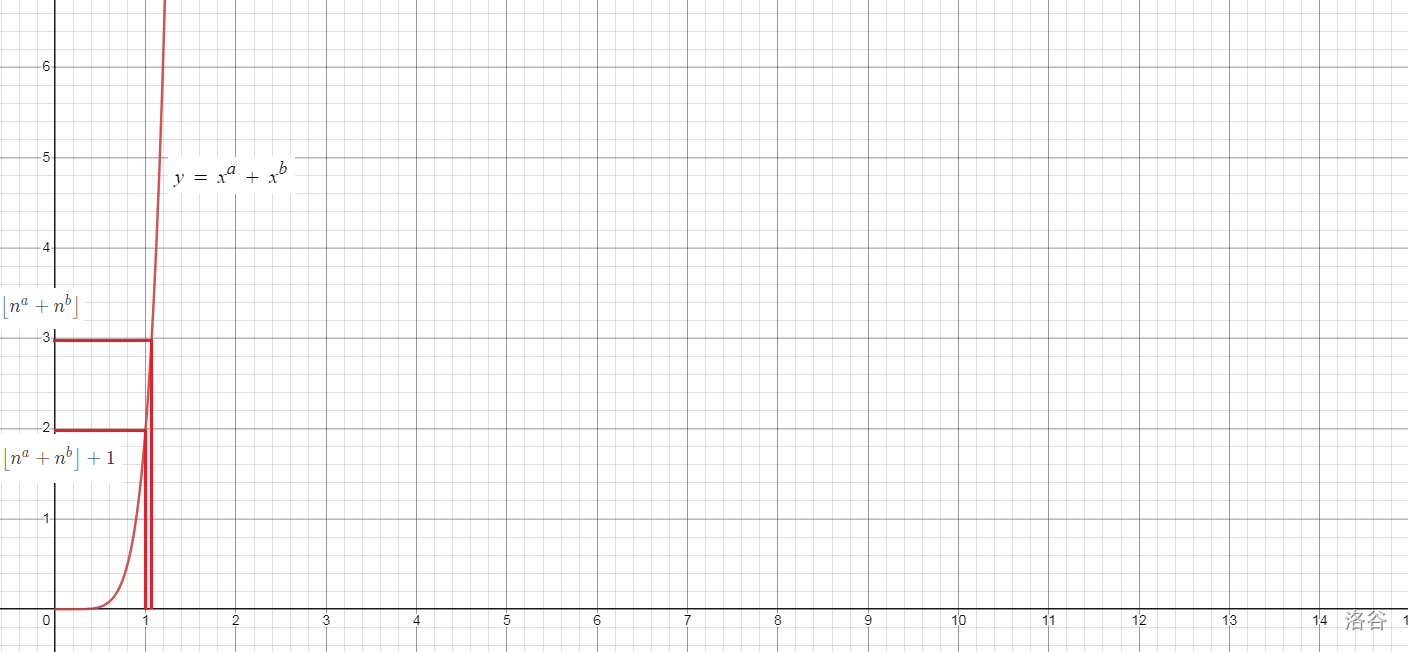
我们可以发现，\(\left \lfloor {n ^ a + n ^ b} \right \rfloor\) 和 \(\left \lfloor {n ^ a + n ^ b} \right \rfloor + 1\) 这两个点的 \(x\) 值靠的非常近，他们中间的曲线近似可以看做直线，因此我们可以把它当做直线斜率。

计算斜率的方法为求导。我们将 \(f(x)\) 的导函数称为 \((x)'\)，那么 \((x ^ a + x ^ b)' = (x^a)' + (x ^ b)' = a x^{a - 1} + b x ^ {b - 1}\) 。

然后将 \(\left \lfloor {n ^ a + n ^ b} \right \rfloor\) 和 \(\left \lfloor {n ^ a + n ^ b} \right \rfloor + 1\) 带入并化简得到答案为 \(\frac{1}{a x^{a - 1} + b x ^ {b - 1}}\) （当然也可以用 \(\tan\) 啦）

代码

#include <iostream>
#include <cstring>
#include <cstdio>
#include <algorithm>
#include <cmath>
using namespace std;
namespace Mker
{
	#define uint unsigned int
	uint sd;int op;
	inline void init() {scanf("%u %d", &sd, &op);}
	inline uint uint_rand()
	{
		sd ^= sd << 13;
		sd ^= sd >> 7;
		sd ^= sd << 11;
		return sd;
	}
	inline double get_n()
	{
		double x = (double) (uint_rand() % 100000) / 100000;
		return x + 4;
	}
	inline double get_k()
	{
		double x = (double) (uint_rand() % 100000) / 100000;
		return (x + 1) * 5;
	}
	inline void read(double &n,double &a, double &b)
	{
		n = get_n(); a = get_k();
		if (op) b = a;
		else b = get_k();
	}
}
using namespace Mker;
double n, a, b;
int T;
int main()
{
    scanf("%d", &T);
    init();
    double res = 0;
    while (T -- )
    {
        read(n, a, b);
        res += (double)1.00 / (a * pow(n, a - 1) + b * pow(n, b - 1));
    }
    printf("%.5lf\n", res);
    return 0;
}