文心一言 VS 讯飞星火 VS chatgpt (208)-- 算法导论15.4 5题
五、设计一个 O($n^2$) 时间的算法,求一个 n 个数的序列的最长单调递增子序列。要写代码的时候,请用go语言。
文心一言,抛panic:
在 Go 语言中设计一个 O(n^2) 时间复杂度的算法来求一个 n 个数的序列的最长单调递增子序列(Longest Increasing Subsequence, LIS)可以使用动态规划的方法。以下是一个实现示例:
package mainimport ("fmt")// LIS 使用动态规划来求一个序列的最长单调递增子序列func LIS(nums []int) []int {n := len(nums)if n == 0 {return []int{}}// dp[i] 表示以 nums[i] 结尾的最长递增子序列的长度dp := make([]int, n)// 初始化 dp 数组,每个元素自身构成一个长度为 1 的递增子序列for i := 0; i < n; i++ {dp[i] = 1}// 初始化最长递增子序列的末尾元素数组lis := make([]int, n)// 最长递增子序列的长度maxLen := 1// 最长递增子序列的末尾元素索引maxIndex := 0for i := 1; i < n; i++ {for j := 0; j < i; j++ {// 如果 nums[i] 大于 nums[j],则考虑将 nums[i] 添加到以 nums[j] 结尾的递增子序列if nums[i] > nums[j] && dp[i] < dp[j]+1 {dp[i] = dp[j] + 1lis[i] = j // 记录状态转移路径}}// 更新最长递增子序列的长度和末尾元素索引if dp[i] > maxLen {maxLen = dp[i]maxIndex = i}}// 根据状态转移路径反向构建最长递增子序列result := make([]int, maxLen)for i := maxIndex; i >= 0; i = lis[i] {result[maxLen-1-i] = nums[i]}return result}func main() {nums := []int{10, 9, 2, 5, 3, 7, 101, 18}lis := LIS(nums)fmt.Println("The longest increasing subsequence is:", lis)}
这个算法的时间复杂度是 O(n^2),其中 n 是序列的长度。我们创建了一个 dp 数组来存储以每个元素结尾的最长递增子序列的长度,并通过比较每个元素和它之前的元素来更新 dp 数组。我们也创建了一个 lis 数组来记录状态转移的路径,以便在算法结束时反向构建出最长递增子序列。
当 dp[i] 的值更新时,我们记录下是哪个 dp[j] 转移过来的,即 lis[i] = j。这样,在构建最长递增子序列时,我们可以从 maxIndex(最长递增子序列的末尾元素索引)开始,根据 lis 数组反向追溯,得到整个子序列。
在 main 函数中,我们调用 LIS 函数并打印出最长递增子序列。


讯飞星火,代码正常运行:
在Go语言中,我们可以使用动态规划来解决这个问题。以下是实现最长单调递增子序列的代码:
package mainimport "fmt"func max(a, b int) int {if a > b {return a}return b}func longestIncreasingSubsequence(nums []int) int {n := len(nums)dp := make([]int, n)for i := range dp {dp[i] = 1}for i := 1; i < n; i++ {for j := 0; j < i; j++ {if nums[i] > nums[j] {dp[i] = max(dp[i], dp[j]+1)}}}maxLen := 0for _, v := range dp {maxLen = max(maxLen, v)}return maxLen}func main() {nums := []int{10, 9, 2, 5, 3, 7, 101, 18}fmt.Println("Length of Longest Increasing Subsequence is", longestIncreasingSubsequence(nums))}
在这个程序中,我们首先定义了一个一维数组dp,其中dp[i]表示以第i个元素结尾的最长递增子序列的长度。然后,我们遍历数组,对于每个元素,我们都检查它之前的所有元素,如果当前元素大于之前的某个元素,那么我们就更新dp[i]的值。最后,我们返回dp数组中的最大值,这就是最长递增子序列的长度。

360智脑,代码正常运行:
以下是一个使用Go语言实现的O(n^2)时间的算法,用于求解一个n个数的序列的最长单调递增子序列:
package mainimport "fmt"func longestMonotonicSubsequence(X []int, n int) int {// 初始化dp数组dp := make([]int, n+1)for i := range dp {dp[i] = 1}// 从第二个元素开始遍历for i := 1; i < n; i++ {for j := 0; j < i; j++ {// 如果X[i]大于X[j],并且dp[i]小于dp[j]+1if X[i] > X[j] && dp[i] < dp[j]+1 {dp[i] = dp[j] + 1}}}// 找到dp数组中的最大值max := 0for _, v := range dp {if v > max {max = v}}return max}func main() {X := []int{10, 22, 9, 33, 21, 50, 41, 60}n := len(X)fmt.Println(longestMonotonicSubsequence(X, n))}
在这个算法中,我们使用了一个动态规划的方法。我们首先初始化一个dp数组,其中dp[i]表示序列X中以X[i]结尾的最长单调递增子序列的长度。然后,我们从第二个元素开始遍历X,对于每个元素X[i],我们检查它是否大于之前的元素X[j],并且dp[i]是否小于dp[j]+1。如果是,我们就更新dp[i]为dp[j]+1。最后,我们找到dp数组中的最大值,即为所求的最长单调递增子序列的长度。

智谱清言,代码正常运行:
在计算机科学中,最长单调递增子序列(Longest Monotonically Increasing Subsequence,简称 LIS)问题可以通过动态规划在 O($n^2$)的时间内解决。下面是一个使用 Go 语言实现的 O(n^2) 动态规划算法来解决最长单调递增子序列问题:
package mainimport ("fmt")// lis 函数计算最长单调递增子序列的长度func lis(nums []int) int {if len(nums) == 0 {return 0}// dp[i] 表示以 nums[i] 结尾的最长单调递增子序列的长度dp := make([]int, len(nums))// 初始化dp数组,每个元素的值都是1,因为每个数字本身都可以构成一个长度为1的递增子序列for i := range dp {dp[i] = 1}// 动态规划填表for i := 1; i < len(nums); i++ {for j := 0; j < i; j++ {if nums[i] > nums[j] {dp[i] = max(dp[i], dp[j]+1)}}}// 找出dp数组中的最大值,即为最长单调递增子序列的长度maxLength := 0for _, length := range dp {maxLength = max(maxLength, length)}return maxLength}// max 函数返回两个整数中的最大值func max(a, b int) int {if a > b {return a}return b}func main() {// 测试数据nums := []int{10, 9, 2, 5, 3, 7, 101, 18}fmt.Println("The length of the longest increasing subsequence is:", lis(nums))}
这段代码首先初始化一个动态规划数组 dp,其中 dp[i] 表示以 nums[i] 结尾的最长单调递增子序列的长度。然后,它通过两层循环来填充这个数组,如果在 nums 中的某个较小的元素 nums[j] 之后有元素 nums[i],则 dp[i] 可以更新为 dp[j] + 1。最后,它遍历 dp 数组以找到最大的值,这个值就是最长单调递增子序列的长度。
请注意,尽管这个算法是 O(n^2) 的,但对于较大的数据集,它可能不是最优的。在实际应用中,可以考虑使用二分搜索优化算法,将时间复杂度降低到 O(nlogn)。

天工,代码正常运行:
以下是一个使用动态规划算法来找出一个包含 n 个元素的序列的最长单调递增子序列(LIS)的 Go 语言实现。这个算法的时间复杂度是 O(n^2)。
package mainimport "fmt"// findLISLength 使用动态规划找出给定数组的最长单调递增子序列的长度。func findLISLength(nums []int) int {if len(nums) == 0 {return 0}dp := make([]int, len(nums))dp[0] = 1 // 初始化第一个元素的 LIS 为 1。for i := 1; i < len(nums); i++ {for j := 0; j < i; j++ {if nums[i] > nums[j] {dp[i] = max(dp[i], dp[j]+1)}}}// 找到最长 LIS 长度。var maxLen intfor _, length := range dp {if length > maxLen {maxLen = length}}return maxLen}// max 返回两个整数中较大的一个。func max(a, b int) int {if a >= b {return a}return b}func main() {nums := []int{10, 22, 9, 33, 21, 50, 30, 60, 80}length := findLISLength(nums)fmt.Printf("Length of LIS: %d\n", length)}
这段代码定义了一个 findLISLength 函数,它接受一个整数切片作为输入,并返回该序列的最长单调递增子序列的长度。函数内部使用了一个名为 dp 的动态规划数组,用于存储每个元素在 LIS 中的可能最大长度。通过迭代和比较,逐步构建出整个数组在 LIS 中的长度,最后通过遍历 dp 数组来找到最长的 LIS 长度。
在 main 函数中,有一个示例数组 nums,调用 findLISLength 函数并打印结果。你可以替换 nums 中的值以测试不同的数组。


灵小智,代码正常运行:
Sure! 下面是一个使用Go语言实现的O($n^2$)时间复杂度的算法来求解一个n个数的序列的最长单调递增子序列。
package mainimport ("fmt")func longestIncreasingSubsequence(nums []int) []int {length := len(nums)dp := make([]int, length)for i := 0; i < length; i++ {dp[i] = 1}for i := 1; i < length; i++ {for j := 0; j < i; j++ {if nums[i] > nums[j] && dp[i] < dp[j]+1 {dp[i] = dp[j] + 1}}}maxLen := 0endIndex := 0for i := 0; i < length; i++ {if dp[i] > maxLen {maxLen = dp[i]endIndex = i}}result := make([]int, maxLen)result[maxLen-1] = nums[endIndex]maxLen--endIndex--for i := endIndex; i >= 0; i-- {if nums[i] < nums[endIndex] && dp[i] == maxLen {result[maxLen-1] = nums[i]maxLen--endIndex = i}}return result}func main() {nums := []int{10, 22, 9, 33, 21, 50, 41, 60}lis := longestIncreasingSubsequence(nums)fmt.Println("最长递增子序列为:", lis)}
希望这个算法和代码对你有所帮助!
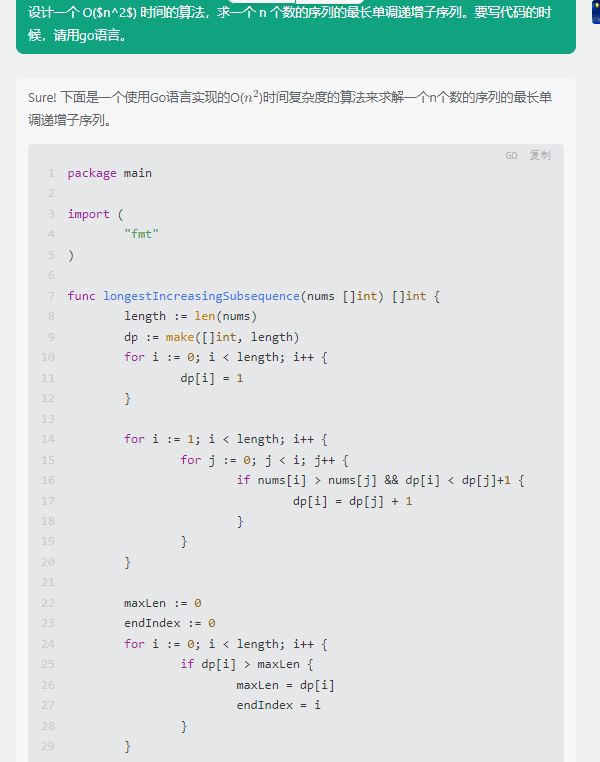

chatgpt,代码正常运行:
要设计一个O(n^2)时间复杂度的算法来求一个n个数的序列的最长单调递增子序列,可以使用动态规划的思想。下面是用Go语言实现的代码:
package mainimport ("fmt")func longestIncreasingSubsequence(nums []int) int {n := len(nums)if n == 0 {return 0}dp := make([]int, n) // dp[i]表示以nums[i]结尾的最长递增子序列长度maxLen := 1 // 最长递增子序列的长度,默认为1for i := 0; i < n; i++ {dp[i] = 1 // 初始化dp数组为1for j := 0; j < i; j++ {if nums[j] < nums[i] && dp[j]+1 > dp[i] {dp[i] = dp[j] + 1 // 更新dp数组}}if dp[i] > maxLen {maxLen = dp[i]}}return maxLen}func main() {nums := []int{10, 22, 9, 33, 21, 50, 41, 60}fmt.Println("最长递增子序列长度:", longestIncreasingSubsequence(nums))}
该代码使用动态规划算法,定义dp数组表示以每个位置元素结尾的最长递增子序列长度。初始化dp数组为1,并在遍历过程中更新dp值。最后返回dp数组中的最大值作为最长递增子序列的长度。
该算法的时间复杂度为O(n^2),因为需要两层循环来遍历所有可能的子序列。
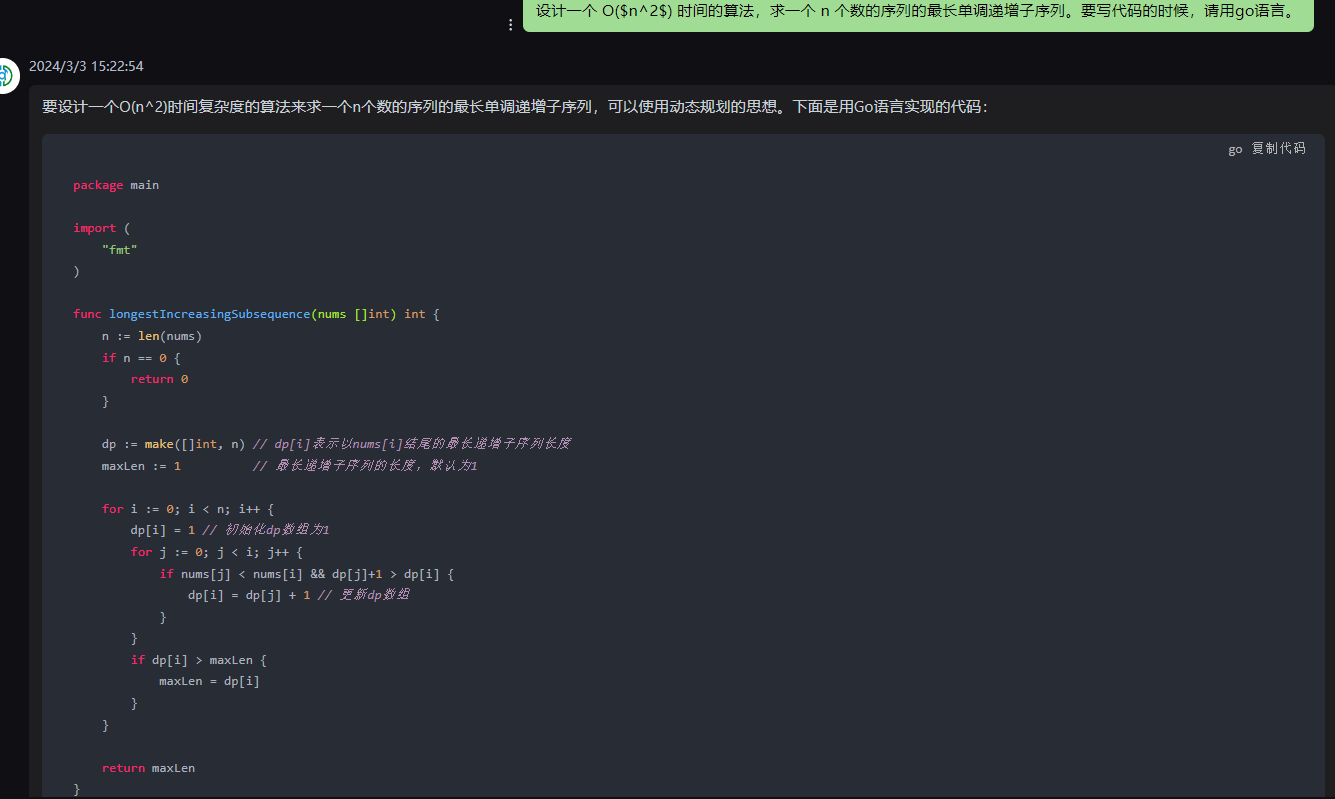

kimi,代码正常运行:
为了在 O(n^2) 时间内找到一个序列的最长单调递增子序列(LIS),我们可以使用一个经典的动态规划方法。这个算法的核心思想是维护一个数组 lis,其中 lis[i] 表示以第 i 个元素结尾的最长递增子序列的长度。对于每个元素,我们需要检查它之前的所有元素,如果当前元素大于之前的某个元素,我们更新 lis 数组。
以下是使用 Go 语言实现的 O(n^2) 时间复杂度的 LIS 算法:
package mainimport ("fmt")// LIS 函数计算序列的最长单调递增子序列的长度func LIS(seq []int) int {n := len(seq)lis := make([]int, n)maxLIS := 0// 初始化 lis 数组,每个元素的 LIS 长度初始为 1for i := range lis {lis[i] = 1}// 遍历序列,更新 lis 数组for i := 1; i < n; i++ {for j := 0; j < i; j++ {if seq[i] > seq[j] && lis[i] < lis[j]+1 {lis[i] = lis[j] + 1}}// 更新最大 LIS 长度if lis[i] > maxLIS {maxLIS = lis[i]}}return maxLIS}func main() {seq := []int{10, 9, 2, 5, 3, 7, 101, 18}lisLength := LIS(seq)fmt.Printf("Length of the Longest Increasing Subsequence is: %d\n", lisLength)}
在这个实现中,我们首先初始化 lis 数组,使得每个元素的 LIS 长度初始为 1。然后,我们使用两层循环来更新 lis 数组。外层循环遍历序列中的每个元素,内层循环检查当前元素之前的所有元素。如果找到一个较小的元素,我们尝试更新当前元素的 LIS 长度。最后,我们记录并返回最大的 LIS 长度。
这个算法的时间复杂度是 O(n^2),因为我们需要对序列中的每个元素进行两次遍历。
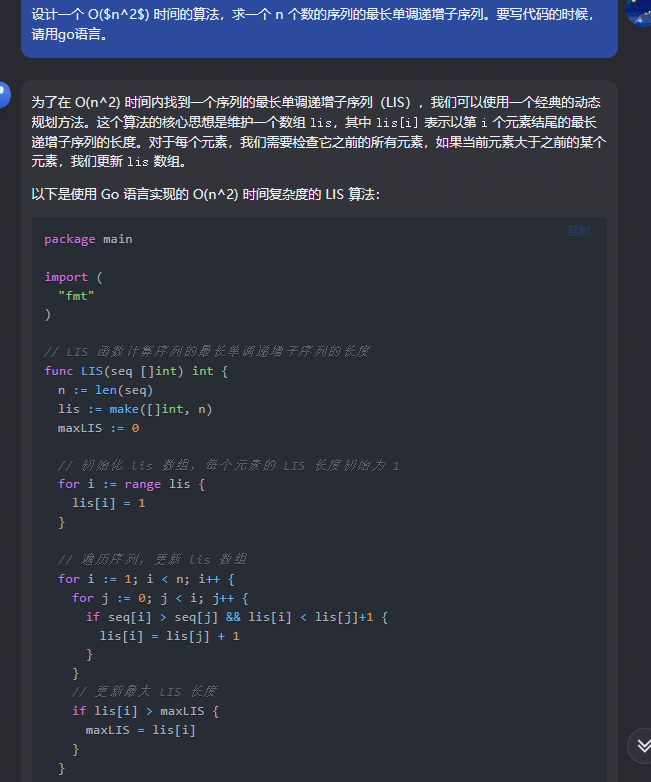

混元,代码正常运行:
以下是使用 Go 语言实现的一个 O(n^2) 时间复杂度的算法,用于求一个 n 个数的序列的最长单调递增子序列:
package mainimport ("fmt")func longestIncreasingSubsequence(arr []int) int {n := len(arr)dp := make([]int, n)for i := range dp {dp[i] = 1}for i := 1; i < n; i++ {for j := 0; j < i; j++ {if arr[i] > arr[j] {dp[i] = max(dp[i], dp[j]+1)}}}maxLength := 0for _, val := range dp {maxLength = max(maxLength, val)}return maxLength}func max(a, b int) int {if a > b {return a}return b}func main() {arr := []int{10, 22, 9, 33, 21, 50, 41, 60, 80}fmt.Printf("The length of the longest increasing subsequence is: %d\n", longestIncreasingSubsequence(arr))}
这个实现使用动态规划方法。dp[i] 表示以 arr[i] 结尾的最长单调递增子序列的长度。对于每个元素 arr[i],我们遍历其之前的所有元素 arr[j],如果 arr[i] > arr[j],则更新 dp[i] 为 max(dp[i], dp[j]+1)。最后,我们返回 dp 数组中的最大值,即为最长单调递增子序列的长度。
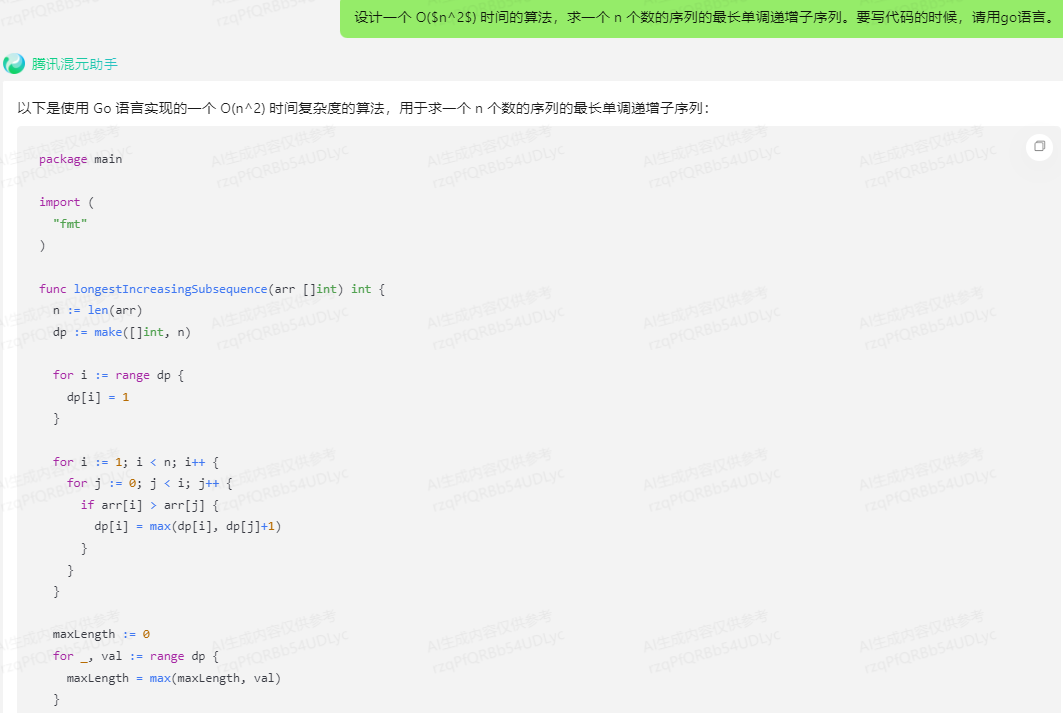

文心一言 VS 讯飞星火 VS chatgpt (208)-- 算法导论15.4 5题的更多相关文章
- 【对比】文心一言对飚ChatGPT实操对比体验
前言 缘由 百度[文心一言]体验申请通过 本狗中午干饭时,天降短信,告知可以体验文心一言,苦等一个月的实操终于到来.心中这好奇的对比心理油然而生,到底是老美的[ChatGPT]厉害,还是咱度娘的[文心 ...
- 【个人首测】百度文心一言 VS ChatGPT GPT-4
昨天我写了一篇文章GPT-4牛是牛,但这几天先别急,文中我测试了用GPT-4回答ChatGPT 3.5 和 Notion AI的问题,大家期待的图片输入也没有出现. 昨天下午百度发布了文心一言,对标C ...
- 文心一言,通营销之学,成一家之言,百度人工智能AI大数据模型文心一言Python3.10接入
"文心"取自<文心雕龙>一书的开篇,作者刘勰在书中引述了一个古代典故:春秋时期,鲁国有一位名叫孔文子的大夫,他在学问上非常有造诣,但是他的儿子却不学无术,孔文子非常痛心 ...
- 获取了文心一言的内测及与其ChatGPT、GPT-4 对比结果
百度在3月16日召开了关于文心一言(知识增强大语言模型)的发布会,但是会上并没现场展示demo.如果要测试的文心一言 也要获取邀请码,才能进行测试的. 我这边通过预约得到了邀请码,大概是在3月17日晚 ...
- 百度生成式AI产品文心一言邀你体验AI创作新奇迹:百度CEO李彦宏详细透露三大产业将会带来机遇(文末附文心一言个人用户体验测试邀请码获取方法,亲测有效)
目录 中国版ChatGPT上线发布 强大中文理解能力 智能文学创作.商业文案创作 图片.视频智能生成 中国生成式AI三大产业机会 新型云计算公司 行业模型精调公司 应用服务提供商 总结 获取文心一言邀 ...
- 阿里版ChatGPT:通义千问pk文心一言
随着 ChatGPT 热潮卷起来,百度发布了文心一言.Google 发布了 Bard,「阿里云」官方终于也宣布了,旗下的 AI 大模型"通义千问"正式开启测试! 申请地址:http ...
- 基于讯飞语音API应用开发之——离线词典构建
最近实习在做一个跟语音相关的项目,就在度娘上搜索了很多关于语音的API,顺藤摸瓜找到了科大讯飞,虽然度娘自家也有语音识别.语义理解这块,但感觉应该不是很好用,毕竟之前用过百度地图的API,有问题也找不 ...
- android用讯飞实现TTS语音合成 实现中文版
Android系统从1.6版本开始就支持TTS(Text-To-Speech),即语音合成.但是android系统默认的TTS引擎:Pic TTS不支持中文.所以我们得安装自己的TTS引擎和语音包. ...
- android讯飞语音开发常遇到的问题
场景:android项目中共使用了3个语音组件:在线语音听写.离线语音合成.离线语音识别 11208:遇到这个错误,授权应用失败,先检查装机量(3台测试权限),以及appid的申请时间(35天期限), ...
- 初探机器学习之使用讯飞TTS服务实现在线语音合成
最近在调研使用各个云平台提供的AI服务,有个语音合成的需求因此就使用了一下科大讯飞的TTS服务,也用.NET Core写了一个小示例,下面就是这个小示例及其相关背景知识的介绍. 一.什么是语音合成(T ...
随机推荐
- Go基础之指针
Go语言中的指针 目录 Go语言中的指针 一.Go语言中的指针介绍 1.1 指针介绍 1.2 基本语法 1.3 声明和初始化 1.4 Go 指针的3个重要概念 1.4.1 指针地址(Pointer A ...
- Leetcode 面试题22. 链表中倒数第k个节点 Java语言求解
题目链接 https://leetcode-cn.com/problems/lian-biao-zhong-dao-shu-di-kge-jie-dian-lcof/ 题目内容 输入一个链表,输出该链 ...
- Unity2019使用Gradle命令行(编译)出安卓包
在我所经历的项目组中有这几种方法来生成APK 直接在Unity生成APK,可以接入SDK 使用Unity导出Android Studio工程手动生成APK 使用Unity导出Android Studi ...
- NFS实现部署Linux文件共享
NFS 即网络文件系统,是一种使用于分布式文件系统的协议,由Sun公司开发,于1984年向外公布,功能是通过网络让不同的机器,不同的操作系统能够彼此分享各自的数据,让应用程序在客户端通过网络访问位于服 ...
- php批量更新多条数据
/** * @param $table 表名 * @param array $multipleData 拼接的批量更新的数组格式: * $students = [['id' => 1, 'cit ...
- (python)每日代码||2024.1.18||元组中的列表成员可以改变内容,不可以改变该列表成员
t = ([1,2,3],[2,3,4],3) print(t) t[0][1]=9 print(t) # ~ t[2]=9#TypeError: 'tuple' object does not su ...
- 零基础入门学习Java课堂笔记 ——day04
Java数组 1.数组概述 定义:数组是相同类型的有序集合,同一组同一类型的数据可以按照先后次序排列组合在一起,其中一个数据可以称为元素,每个数组元素可以通过一个下表访问它们 2.数组声明创建 dat ...
- 阿里二面:SpringBoot可以同时处理多少个请求?当场懵了。。。。
SpringBoot以其简洁高效的开发方式和强大的内嵌容器特性,为开发者提供了构建高性能后端服务的便利.然而,当面临高并发场景时,理解并合理配置Spring Boot应用以达到最佳的并发处理能力至关重 ...
- DBGRIDEH 底部多列 发现
1.设置底部行数 2.点击footers 单独对每一行进行设置 3.单独对这两行 进行设置 5.看下辅助 所以用的时候可以这样用:WeiTopTradeShow.FieldColumns['top_x ...
- linux统计文件大小-以KB、MB、GB、TB为单位
fileSize=`hadoop fs -ls /data/internetLog/home/DPI/idc/20180806/*201808062[0-2]* | awk 'BEGIN{ sum=0 ...
