【集成模型】Bootstrap Aggregating（Bagging）

0 - 思想　　

　　如下图所示，Bagging（Bootstrap Aggregating）的基本思想是，从训练数据集中有返回的抽象m次形成m个子数据集（bootstrapping），对于每一个子数据集训练一个基础分类器，最后将它们的结果综合起来获得最终输出。

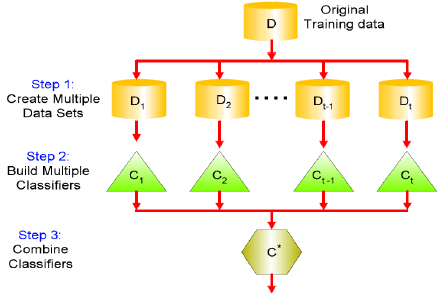
1 - 特点

　　Bagging需要不同的/独立的（diverse/independent）基础模型，因此太过稳定的模型不适合这种集成方法，例如：

• KNN是稳定的
• 决策树是不稳定的，特别是未剪枝的决策树（因为对于每一份数据的拟合可能很不一样）

　　此外，集成模型的性能在基础模型的数量达到一定规模之后，将收敛。

2 - 随机森林（Random Forest）

　　一类最经典的Bagging集成模型是随机森林（Random Forest），其中通过如下两个点来确保随机性（即确保不同基础模型之间的差异性）：

• 每一棵树都使用一个子数据集进行训练（a bootstrap sample of data）
• 每一个结点的最优分割加入了随机化，具体有如下三种方法
  • 从全部的$m$个属性中随机选取$d$个属性，计算它们的信息增益再选择最优的分割；
  • 计算$L$个随机属性的线性组合，线性组合的权重从$[-1,1]$中随机采样（这一种方法不太理解）；
  • 计算全部$m$个属性的信息增益，而后选择最高的$d$个属性，再从中随机选取一个属性进行分割。

3 - 总结

1. Bagging的工作原理是减少预测方差

简单分析预测结果，可以知道Bagging有预测错误概率的上界

• 假设对于基础模型$i$，其预测错误的概率为$P(h_i(x)\neq f(x))=\epsilon $
• 并且取预测最多的类别最为最终结果，表示为$H(x)=sign\left(\sum_{i=1}^T h_i(x) \right )$
• 那么最终预测错误的概率可以表示为（利用Hoeffding inequality）$P(H(x)\neq f(x))=\sum_{k=0}^{\left \lfloor T/2 \right \rfloor}\binom{T}{k}(1-\epsilon)^k\epsilon^{T-k}\leq exp\left(-\frac{1}{2}T(2\epsilon-1)^2 \right )$
2. Bagging很适合并行处理