逻辑回归（Logistic Regression）二分类原理及python实现

本文目录：

1. sigmoid function (logistic function)

2. 逻辑回归二分类模型

3. 神经网络做二分类问题

4. python实现神经网络做二分类问题

-----------------------------------------------------------------------------------

1. sigmoid unit 

对于一个输入样本$X(x_1,x_2, ..., x_n)$，sigmoid单元先计算$x_1,x_2, ..., x_n$的线性组合：

$z = {{\bf{w}}^T}{\bf{x}} = {w_1}{x_1} + {w_2}{x_2} + ... + {w_n}{x_n}$

然后把结果$z$输入到sigmoid函数：

$\sigma (z) = \frac{1}{{1 + {e^{ - z}}}}$

sigmoid函数图像：

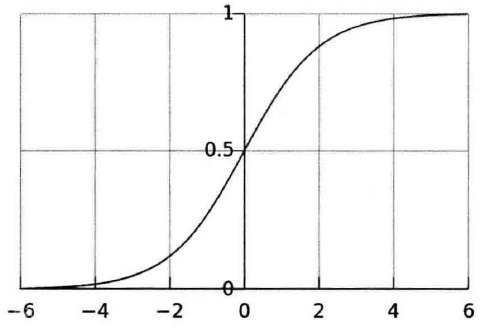
sigmoid函数有个很有用的特征，就是它的导数很容易用它的输出表示，即

$\frac{{\partial \sigma (z)}}{{\partial z}} = \frac{{{e^{ - z}}}}{{{{(1 + {e^{ - z}})}^2}}} = \frac{1}{{1 + {e^{ - z}}}} \cdot \frac{{{e^{ - z}}}}{{1 + {e^{ - z}}}} = \frac{1}{{1 + {e^{ - z}}}} \cdot (1 - \frac{1}{{1 + {e^{ - z}}}}) = \sigma (z)(1 - \sigma (z))\begin{array}{*{20}{c}}
{} & {} & {} & {(1)} \\
\end{array}$

2. 逻辑回归二分类模型

把sigmoid函数应用到二分类中，当$\sigma(z)>=0.5$，输出标签$y=1$；当$\sigma(z)<0.5$，输出标签$y=0$。并定义如下条件概率：

$P\{ Y = 1|\bf{x}\} = p(x) = \frac{1}{{1 + {e^{ - {{\bf{w}}^T}\bf{x}}}}}$

$P\{ Y = 0|\bf{x}\} = 1 - p(\bf{x}) = \frac{{{e^{ - {{\bf{w}}^T}\bf{x}}}}}{{1 + {e^{ - {{\bf{w}}^T}\bf{x}}}}}$

一个事件的几率（$odds$）是指该事件发生的概率和该事件不发生的概率的比值。如果事件发生的概率是$p$，那么该事件的几率是$\frac{p}{1-p}$，该事件的对数几率（$log$ $odds$）或$logit$函数是$logit(p)=ln\frac{p}{1-p}$。在逻辑回归二分类模型中，事件的对数几率是

$\ln \frac{{P\{ Y = 1|\bf{x}\} }}{{P\{ Y = 0|\bf{x}\} }} = \ln \frac{{p(x)}}{{1 - p(\bf{x})}} = \ln ({e^{{{\bf{w}}^T}\bf{x}}}) = {{\bf{w}}^T}\bf{x}$

上式表明，在逻辑回归二分类模型中，输出$y=1$的对数几率是输入$\bf{x}$的线性函数。

在逻辑回归二分类模型中，对于给定的数据集$T = \{ ({{\bf{x}}_1},{y_1}),({{\bf{x}}_2},{y_2}),...,({{\bf{x}}_n},{y_n})\}$，可以应用极大似然估计法估计模型参数${{\bf{w}}^T} = ({w_1},{w_2},...,{w_n})$。

设：

$\begin{array}{l}
P\{ Y = 1|\bf{x}\} = \sigma ({{\bf{w}}^T}{\bf{x}}) \\
P\{ Y = 0|\bf{x}\} = 1 - \sigma ({{\bf{w}}^T}{\bf{x}}) \\
\end{array}$

似然函数为：

$\prod\limits_{i = 1}^n {{{[\sigma ({{\bf{w}}^T}{{\bf{x}}_i})]}^{{y_i}}}} {[1 - \sigma ({{\bf{w}}^T}{{\bf{x}}_i})]^{1 - {y_i}}}$

对数似然函数为：

$L({\bf{w}}) = \sum\limits_{i = 1}^n {[{y_i}\log } \sigma ({{\bf{w}}^T}{{\bf{x}}_i}) + (1 - {y_i})\log (1 - \sigma ({{\bf{w}}^T}{{\bf{x}}_i}))]$

对$L({\bf{w}})$取极大值，

$\frac{{\partial L({\bf{w}})}}{{\partial{w_j}}} = \sum\limits_{i = 1}^n {[\frac{{{y_i}}}{{\sigma ({{\bf{w}}^T}{{\bf{x}}_i})}}} - \frac{{1 - {y_i}}}{{1 - \sigma ({{\bf{w}}^T}{{\bf{x}}_i})}}]\frac{{\partial \sigma ({{\bf{w}}^T}{{\bf{x}}_i})}}{{\partial ({{\bf{w}}^T}{{\bf{x}}_i})}}\frac{{\partial ({{\bf{w}}^T}{{\bf{x}}_i})}}{{\partial {w_j}}}$

应用式(1)，有

$\frac{{\partial L({\bf{w}})}}{{\partial{w_j}}} = \sum\limits_{i = 1}^n {[\frac{{{y_i} - \sigma ({{\bf{w}}^T}{{\bf{x}}_i})}}{{\sigma ({{\bf{w}}^T}{{\bf{x}}_i})[1 - \sigma ({{\bf{w}}^T}{{\bf{x}}_i})]}}} ] \cdot \sigma ({{\bf{w}}^T}{{\bf{x}}_i})[1 - \sigma ({{\bf{w}}^T}{{\bf{x}}_i})] \cdot {x_{ij}}$

$\frac{{\partial L({\bf{w}})}}{{\partial{w_j}}} = \sum\limits_{i = 1}^n [ {y_i} - \sigma ({{\bf{w}}^T}{{\bf{x}}_i})] \cdot {x_{ij}}$

令$\frac{{\partial L({\bf{w}})}}{{{w_j}}}=0$即可得到参数${\bf{w}}$的估计值。

3. 神经网络做二分类问题，交叉熵损失函数

在阈值函数是sigmoid函数的神经网络中，针对二分类问题，交叉熵损失函数是比较合适的损失函数，其形式为（和上一节的对数似然函数只相差一个负号）：

$C =- \frac{1}{n}\sum\limits_{i = 1}^n {[{y_i}\log } \sigma ({{\bf{w}}^T}{{\bf{x}}_i}) + (1 - {y_i})\log (1 - \sigma ({{\bf{w}}^T}{{\bf{x}}_i}))]$

在神经网络的训练过程中，权重的迭代过程为：

$w_j^{k + 1} = w_j^k - \eta \frac{{\partial C}}{{\partial w_j^k}}$

在损失函数是交叉熵损失函数的情况下，

$\frac{{\partial C}}{{\partial w_j^k}} = \sum\limits_{i = 1}^n [ \sigma ({{\bf{w}}^T}{{\bf{x}}_i}) - {y_i}] \cdot {x_{ij}} = ({{\bf{x}}^T}[\sigma ({{\bf{w}}^T}{\bf{x}}) - {\bf{y}}] )_j= ({{\bf{x}}^T}{\bf{e}})_j$

其中，${\bf{y}}$是由样本标签构成的列向量，等号后的两个式子的下标$j$表示向量的第$j$个分量。

4. python实现神经网络做二分类问题

神经网络结构：一个sigmoid单元

训练数据：总共500个训练样本，链接https://pan.baidu.com/s/1qWugzIzdN9qZUnEw4kWcww，提取码：ncuj

损失函数：交叉熵损失函数

代码如下：

import numpy as np
import matplotlib.pyplot as plt

class Logister():
    def __init__(self, path):
        self.path = path

    def file2matrix(self, delimiter):
        fp = open(self.path, 'r')
        content = fp.read()              # content现在是一行字符串，该字符串包含文件所有内容
        fp.close()
        rowlist = content.splitlines()   # 按行转换为一维表
        # 逐行遍历
        # 结果按分隔符分割为行向量
        recordlist = [list(map(float, row.split(delimiter))) for row in rowlist if row.strip()]
        return np.mat(recordlist)

    def drawScatterbyLabel(self, dataSet):
        m, n = dataSet.shape
        target = np.array(dataSet[:, -1])
        target = target.squeeze()        # 把二维数据变为一维数据
        for i in range(m):
            if target[i] == 0:
                plt.scatter(dataSet[i, 0], dataSet[i, 1], c='blue', marker='o')
            if target[i] == 1:
                plt.scatter(dataSet[i, 0], dataSet[i, 1], c='red', marker='o')

    def buildMat(self, dataSet):
        m, n = dataSet.shape
        dataMat = np.zeros((m, n))
        dataMat[:, 0] = 1
        dataMat[:, 1:] = dataSet[:, :-1]
        return dataMat

    def logistic(self, wTx):
        return 1.0/(1.0 + np.exp(-wTx))

    def classfier(self, testData, weights):
        prob = self.logistic(sum(testData*weights))   # 求取概率--判别算法
        if prob > 0.5:
            return 1
        else:
            return 0

if __name__ == '__main__':
    logis = Logister('testSet.txt')

    print('1. 导入数据')
    inputData = logis.file2matrix('\t')
    target = inputData[:, -1]
    m, n = inputData.shape
    print('size of input data: {} * {}'.format(m, n))

    print('2. 按分类绘制散点图')
    logis.drawScatterbyLabel(inputData)

    print('3. 构建系数矩阵')
    dataMat = logis.buildMat(inputData)

    alpha = 0.1                 # learning rate
    steps = 600                 # total iterations
    weights = np.ones((n, 1))   # initialize weights
    weightlist = []

    print('4. 训练模型')
    for k in range(steps):
        output = logis.logistic(dataMat * np.mat(weights))
        errors = target - output
        print('iteration: {}  error_norm: {}'.format(k, np.linalg.norm(errors)))
        weights = weights + alpha*dataMat.T*errors  # 梯度下降
        weightlist.append(weights)

    print('5. 画出训练过程')
    X = np.linspace(-5, 15, 301)
    weights = np.array(weights)
    length = len(weightlist)
    for idx in range(length):
        if idx % 100 == 0:
            weight = np.array(weightlist[idx])
            Y = -(weight[0] + X * weight[1]) / weight[2]
            plt.plot(X, Y)
            plt.annotate('hplane:' + str(idx), xy=(X[0], Y[0]))
    plt.show()

    print('6. 应用模型到测试数据中')
    testdata = np.mat([-0.147324, 2.874846])           # 测试数据
    m, n = testdata.shape
    testmat = np.zeros((m, n+1))
    testmat[:, 0] = 1
    testmat[:, 1:] = testdata
    print(logis.classfier(testmat, np.mat(weights)))   # weights为前面训练得出的

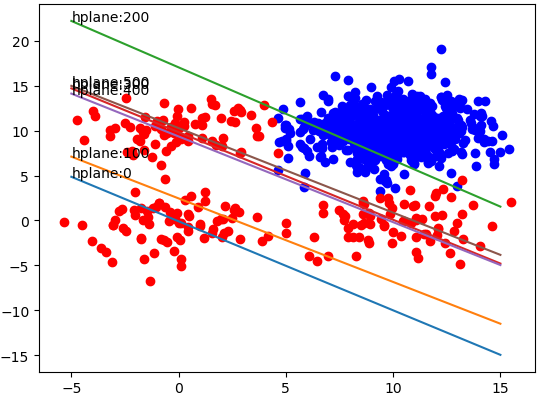
训练600个iterations，每100个iterations输出一次训练结果，如下图：

【参考文献】

[1] 《机器学习》Mitshell，第四章

[2] 《机器学习算法原理与编程实践》郑捷，第五章第二节

[3] Neural Network and Deep Learning，Michael Nielsen，chapter 3