CSPS模拟88-91
感觉自己好菜啊，考得一次不如一次了。。。压力好大，++滚粗感。
模拟88。
T1，sbt，发现离散化后数据范围变为6000，直接跑暴力即可。%%%机房众神斜率优化。
T2，大模拟，考场上只会乱搞骗分。本人菜鸡，只会大力分类讨论。。。
#include<bits/stdc++.h>
using namespace std;
const double eps=5e-;
double f[][],f1[][],f2[][];
double dp[][][][][];
double ans[][];
int a[][],tt[];
int n;
char s1[],s2[],s3[];
double gg;
inline void prans(int id)
{
double gg=1.0;
memset(ans,,sizeof(ans));
for(int j=;j<=;++j)
for(int k=;k<=;++k)
for(int o=;o<=;++o)
for(int l=;l<=;++l)
{
gg-=dp[id][j][k][o][l];
ans[][a[][j]]+=dp[id][j][k][o][l];
ans[][a[][k]]+=dp[id][j][k][o][l];
ans[][a[][o]]+=dp[id][j][k][o][l];
ans[][a[][l]]+=dp[id][j][k][o][l];
}
printf("%.2lf\n",gg*);
for(int i=;i<=;++i)
{
for(int j=;j<=;++j)
{
printf("%.2lf ",ans[i][j]*);
}
puts("");
}
}
inline void init()
{
f[][]=f[][]=f[][]=1.0/;
for(int i=;i<=;++i){
for(int j=;j<=;++j){
if(j)f1[i][j]=f1[i][j-];
f1[i][j]+=f[i][j];
f[i+][j]+=f[i][j]*f[][];
f[i+][j+]+=f[i][j]*f[][];
f[i+][j+]+=f[i][j]*f[][];
}
for(int j=;~j;--j)f2[i][j]=f2[i][j+]+f[i][j];
}
}
void work1(int m,int i,int num,int isw,double g=1.0,int fj=,int fk=,int fo=,int fl=,int jj=,int kk=,int oo=,int ll=)
{
if(m==)
{
if(isw)
{
for(int j=fj;j<=jj;++j)
for(int k=fk;k<=kk;++k)
for(int o=fo;o<=oo;++o)
for(int l=fl;l<=ll;++l)
for(int t=;t<=*num;++t)
dp[i+][min(j+t,)][k][o][l]+=dp[i][j][k][o][l]*f[num][t]*g;
}
else
{
for(int j=fj;j<=jj;++j)
for(int k=fk;k<=kk;++k)
for(int o=fo;o<=oo;++o)
for(int l=fl;l<=ll;++l)
dp[i+][min(j+num,)][k][o][l]+=dp[i][j][k][o][l]*g;
}
}
else if(m==)
{
if(isw)
{
for(int j=fj;j<=jj;++j)
for(int k=fk;k<=kk;++k)
for(int o=fo;o<=oo;++o)
for(int l=fl;l<=ll;++l)
for(int t=;t<=*num;++t)
dp[i+][j][min(k+t,)][o][l]+=dp[i][j][k][o][l]*f[num][t]*g;
}
else
{
for(int j=fj;j<=jj;++j)
for(int k=fk;k<=kk;++k)
for(int o=fo;o<=oo;++o)
for(int l=fl;l<=ll;++l)
dp[i+][j][min(k+num,)][o][l]+=dp[i][j][k][o][l]*g;
}
}
else if(m==)
{
if(isw)
{
for(int j=fj;j<=jj;++j)
for(int k=fk;k<=kk;++k)
for(int o=fo;o<=oo;++o)
for(int l=fl;l<=ll;++l)
for(int t=;t<=*num;++t)
dp[i+][j][k][min(o+t,)][l]+=dp[i][j][k][o][l]*f[num][t]*g;
}
else
{
for(int j=fj;j<=jj;++j)
for(int k=fk;k<=kk;++k)
for(int o=fo;o<=oo;++o)
for(int l=fl;l<=ll;++l)
dp[i+][j][k][min(o+num,)][l]+=dp[i][j][k][o][l]*g;
}
}
else
{
if(isw)
{
for(int j=fj;j<=jj;++j)
for(int k=fk;k<=kk;++k)
for(int o=fo;o<=oo;++o)
for(int l=fl;l<=ll;++l)
for(int t=;t<=*num;++t)
dp[i+][j][k][o][min(l+t,)]+=dp[i][j][k][o][l]*f[num][t]*g;
}
else
{
for(int j=fj;j<=jj;++j)
for(int k=fk;k<=kk;++k)
for(int o=fo;o<=oo;++o)
for(int l=fl;l<=ll;++l)
dp[i+][j][k][o][min(l+num,)]+=dp[i][j][k][o][l]*g;
}
}
}
//////////////////////////////////////////////////分界线work1&2///////////////////////////////////////////////////////////////
void work2(int m,int i,int num,int isw,double g=1.0,int fj=,int fk=,int fo=,int fl=,int jj=,int kk=,int oo=,int ll=)
{
if(m==)
{
if(isw)
{
for(int j=fj;j<=jj;++j)
for(int k=fk;k<=kk;++k)
for(int o=fo;o<=oo;++o)
for(int l=fl;l<=ll;++l)
for(int t=;t<=*num;++t)
dp[i+][max(j-t,)][k][o][l]+=dp[i][j][k][o][l]*f[num][t]*g;
}
else
{
for(int j=fj;j<=jj;++j)
for(int k=fk;k<=kk;++k)
for(int o=fo;o<=oo;++o)
for(int l=fl;l<=ll;++l)
dp[i+][max(j-num,)][k][o][l]+=dp[i][j][k][o][l]*g;
}
}
else if(m==)
{
if(isw)
{
for(int j=fj;j<=jj;++j)
for(int k=fk;k<=kk;++k)
for(int o=fo;o<=oo;++o)
for(int l=fl;l<=ll;++l)
for(int t=;t<=*num;++t)
dp[i+][j][max(k-t,)][o][l]+=dp[i][j][k][o][l]*f[num][t]*g;
}
else
{
for(int j=fj;j<=jj;++j)
for(int k=fk;k<=kk;++k)
for(int o=fo;o<=oo;++o)
for(int l=fl;l<=ll;++l)
dp[i+][j][max(k-num,)][o][l]+=dp[i][j][k][o][l]*g;
}
}
else if(m==)
{
if(isw)
{
for(int j=fj;j<=jj;++j)
for(int k=fk;k<=kk;++k)
for(int o=fo;o<=oo;++o)
for(int l=fl;l<=ll;++l)
for(int t=;t<=*num;++t)
dp[i+][j][k][max(o-t,)][l]+=dp[i][j][k][o][l]*f[num][t]*g;
}
else
{
for(int j=fj;j<=jj;++j)
for(int k=fk;k<=kk;++k)
for(int o=fo;o<=oo;++o)
for(int l=fl;l<=ll;++l)
dp[i+][j][k][max(o-num,)][l]+=dp[i][j][k][o][l]*g;
}
}
else
{
if(isw)
{
for(int j=fj;j<=jj;++j)
for(int k=fk;k<=kk;++k)
for(int o=fo;o<=oo;++o)
for(int l=fl;l<=ll;++l)
for(int t=;t<=*num;++t)
dp[i+][j][k][o][max(l-t,)]+=dp[i][j][k][o][l]*f[num][t]*g;
}
else
{
for(int j=fj;j<=jj;++j)
for(int k=fk;k<=kk;++k)
for(int o=fo;o<=oo;++o)
for(int l=fl;l<=ll;++l)
dp[i+][j][k][o][max(l-num,)]+=dp[i][j][k][o][l]*g;
}
}
} int main()
{
// freopen("da.in","r",stdin);
init();
for(int i=,x;i<=;++i){
scanf("%d%d",&a[i][],&tt[i]);
for(int j=;j;--j){a[i][j-]=a[i][j]/;a[i][j]%=;}
}
dp[][tt[]][tt[]][tt[]][tt[]]=1.0;
scanf("%d",&n);
/*
t1:当前处理点
t2:受影响点
i:当前处理的操作
l2:数字串长度，对？处理
tag:标记是否有问号
tg2:标记是否有=
*/
for(int i=,t1,t2,l2,num,tag,tg2;i<=n;++i)//work2(int m,int i,int num,int isw)
{
// if(i==5)prans(i);
t1=l2=tag=num=tg2=;
scanf("%s%s",s1,s2+);
l2=strlen(s2+);
if(s1[]=='i')t1=;
else if(s1[]=='p')t1=;
else if(s1[]=='a')t1=;
else t1=;
switch(s2[])
{
case '<':
{
scanf("%d",&tg2);
if(l2==)++tg2;
scanf("%s%s",s1,s2+);
if(s1[]=='i')t2=;
else if(s1[]=='p')t2=;
else if(s1[]=='a')t2=;
else t2=; l2=strlen(s2+);
for(int j=;j<l2;++j)num=num*+s2[j]-'';
if(s2[l2]=='?')tag=;
else num=num*+s2[l2]-'';
for(int j=;j<=;++j)
for(int k=;k<=;++k)
for(int o=;o<=;++o)
for(int l=;l<=;++l){
if(t1==)
{
for(int tmd=;tmd<=*a[][j];++tmd)
{
if(tmd>=tg2)
{
dp[i+][j][k][o][l]+=dp[i][j][k][o][l]*f[a[][j]][tmd];
continue;
}
if(t2==)
{
if(tag){
for(int t=;t<=num*;++t){
if(s2[]=='+')dp[i+][min(j+t,)][k][o][l]+=dp[i][j][k][o][l]*f[a[][j]][tmd]*f[num][t];
else dp[i+][max(j-t,)][k][o][l]+=dp[i][j][k][o][l]*f[a[][j]][tmd]*f[num][t];
}
}
else
{
if(s2[]=='+')dp[i+][min(j+num,)][k][o][l]+=dp[i][j][k][o][l]*f[a[][j]][tmd];
else dp[i+][max(j-num,)][k][o][l]+=dp[i][j][k][o][l]*f[a[][j]][tmd];
}
}
else if(t2==)
{
if(tag){
for(int t=;t<=num*;++t){
if(s2[]=='+')dp[i+][j][min(k+t,)][o][l]+=dp[i][j][k][o][l]*f[a[][j]][tmd]*f[num][t];
else dp[i+][j][max(k-t,)][o][l]+=dp[i][j][k][o][l]*f[a[][j]][tmd]*f[num][t];
}
}
else
{
if(s2[]=='+')dp[i+][j][min(k+num,)][o][l]+=dp[i][j][k][o][l]*f[a[][j]][tmd];
else dp[i+][j][max(k-num,)][o][l]+=dp[i][j][k][o][l]*f[a[][j]][tmd];
}
}
else if(t2==)
{
if(tag){
for(int t=;t<=num*;++t){
if(s2[]=='+')dp[i+][j][k][min(o+t,)][l]+=dp[i][j][k][o][l]*f[a[][j]][tmd]*f[num][t];
else dp[i+][j][k][max(o-t,)][l]+=dp[i][j][k][o][l]*f[a[][j]][tmd]*f[num][t];
}
}
else
{
if(s2[]=='+')dp[i+][j][k][min(o+num,)][l]+=dp[i][j][k][o][l]*f[a[][j]][tmd];
else dp[i+][j][k][max(o-num,)][l]+=dp[i][j][k][o][l]*f[a[][j]][tmd];
}
}
else
{
if(tag){
for(int t=;t<=num*;++t){
if(s2[]=='+')dp[i+][j][k][o][min(l+t,)]+=dp[i][j][k][o][l]*f[a[][j]][tmd]*f[num][t];
else dp[i+][j][k][o][max(l-t,)]+=dp[i][j][k][o][l]*f[a[][j]][tmd]*f[num][t];
}
}
else
{
if(s2[]=='+')dp[i+][j][k][o][min(l+num,)]+=dp[i][j][k][o][l]*f[a[][j]][tmd];
else dp[i+][j][k][o][max(l-num,)]+=dp[i][j][k][o][l]*f[a[][j]][tmd];
}
}
}
}
else if(t1==)
{
for(int tmd=;tmd<=*a[][k];++tmd)
{
if(tmd>=tg2)
{
dp[i+][j][k][o][l]+=dp[i][j][k][o][l]*f[a[][k]][tmd];
continue;
}
if(t2==)
{
if(tag){
for(int t=;t<=num*;++t){
if(s2[]=='+')dp[i+][min(j+t,)][k][o][l]+=dp[i][j][k][o][l]*f[a[][k]][tmd]*f[num][t];
else dp[i+][max(j-t,)][k][o][l]+=dp[i][j][k][o][l]*f[a[][k]][tmd]*f[num][t];
}
}
else
{
if(s2[]=='+')dp[i+][min(j+num,)][k][o][l]+=dp[i][j][k][o][l]*f[a[][k]][tmd];
else dp[i+][max(j-num,)][k][o][l]+=dp[i][j][k][o][l]*f[a[][k]][tmd];
}
}
else if(t2==)
{
if(tag){
for(int t=;t<=num*;++t){
if(s2[]=='+')dp[i+][j][min(k+t,)][o][l]+=dp[i][j][k][o][l]*f[a[][k]][tmd]*f[num][t];
else dp[i+][j][max(k-t,)][o][l]+=dp[i][j][k][o][l]*f[a[][k]][tmd]*f[num][t];
}
}
else
{
if(s2[]=='+')dp[i+][j][min(k+num,)][o][l]+=dp[i][j][k][o][l]*f[a[][k]][tmd];
else dp[i+][j][max(k-num,)][o][l]+=dp[i][j][k][o][l]*f[a[][k]][tmd];
}
}
else if(t2==)
{
if(tag){
for(int t=;t<=num*;++t){
if(s2[]=='+')dp[i+][j][k][min(o+t,)][l]+=dp[i][j][k][o][l]*f[a[][k]][tmd]*f[num][t];
else dp[i+][j][k][max(o-t,)][l]+=dp[i][j][k][o][l]*f[a[][k]][tmd]*f[num][t];
}
}
else
{
if(s2[]=='+')dp[i+][j][k][min(o+num,)][l]+=dp[i][j][k][o][l]*f[a[][k]][tmd];
else dp[i+][j][k][max(o-num,)][l]+=dp[i][j][k][o][l]*f[a[][k]][tmd];
}
}
else
{
if(tag){
for(int t=;t<=num*;++t){
if(s2[]=='+')dp[i+][j][k][o][min(l+t,)]+=dp[i][j][k][o][l]*f[a[][k]][tmd]*f[num][t];
else dp[i+][j][k][o][max(l-t,)]+=dp[i][j][k][o][l]*f[a[][k]][tmd]*f[num][t];
}
}
else
{
if(s2[]=='+')dp[i+][j][k][o][min(l+num,)]+=dp[i][j][k][o][l]*f[a[][k]][tmd];
else dp[i+][j][k][o][max(l-num,)]+=dp[i][j][k][o][l]*f[a[][k]][tmd];
}
}
}
}
else if(t1==)
{
for(int tmd=;tmd<=*a[][o];++tmd)
{
if(tmd>=tg2)
{
dp[i+][j][k][o][l]+=dp[i][j][k][o][l]*f[a[][o]][tmd];
continue;
}
if(t2==)
{
if(tag){
for(int t=;t<=num*;++t){
if(s2[]=='+')dp[i+][min(j+t,)][k][o][l]+=dp[i][j][k][o][l]*f[a[][o]][tmd]*f[num][t];
else dp[i+][max(j-t,)][k][o][l]+=dp[i][j][k][o][l]*f[a[][o]][tmd]*f[num][t];
}
}
else
{
if(s2[]=='+')dp[i+][min(j+num,)][k][o][l]+=dp[i][j][k][o][l]*f[a[][o]][tmd];
else dp[i+][max(j-num,)][k][o][l]+=dp[i][j][k][o][l]*f[a[][o]][tmd];
}
}
else if(t2==)
{
if(tag){
for(int t=;t<=num*;++t){
if(s2[]=='+')dp[i+][j][min(k+t,)][o][l]+=dp[i][j][k][o][l]*f[a[][o]][tmd]*f[num][t];
else dp[i+][j][max(k-t,)][o][l]+=dp[i][j][k][o][l]*f[a[][o]][tmd]*f[num][t];
}
}
else
{
if(s2[]=='+')dp[i+][j][min(k+num,)][o][l]+=dp[i][j][k][o][l]*f[a[][o]][tmd];
else dp[i+][j][max(k-num,)][o][l]+=dp[i][j][k][o][l]*f[a[][o]][tmd];
}
}
else if(t2==)
{
if(tag){
for(int t=;t<=num*;++t){
if(s2[]=='+')dp[i+][j][k][min(o+t,)][l]+=dp[i][j][k][o][l]*f[a[][o]][tmd]*f[num][t];
else dp[i+][j][k][max(o-t,)][l]+=dp[i][j][k][o][l]*f[a[][o]][tmd]*f[num][t];
}
}
else
{
if(s2[]=='+')dp[i+][j][k][min(o+num,)][l]+=dp[i][j][k][o][l]*f[a[][o]][tmd];
else dp[i+][j][k][max(o-num,)][l]+=dp[i][j][k][o][l]*f[a[][o]][tmd];
}
}
else/////////////////////////////////////////////////////////////////here
{
if(tag){
for(int t=;t<=num*;++t){
// cout<<t<<endl;
if(s2[]=='+')dp[i+][j][k][o][min(l+t,)]+=dp[i][j][k][o][l]*f[a[][o]][tmd]*f[num][t];
else dp[i+][j][k][o][max(l-t,)]+=dp[i][j][k][o][l]*f[a[][o]][tmd]*f[num][t];
}
}
else
{
if(s2[]=='+')dp[i+][j][k][o][min(l+num,)]+=dp[i][j][k][o][l]*f[a[][o]][tmd];
else dp[i+][j][k][o][max(l-num,)]+=dp[i][j][k][o][l]*f[a[][o]][tmd];
}
}
}
}
else
{
for(int tmd=;tmd<=*a[][l];++tmd)
{
if(tmd>=tg2)
{
dp[i+][j][k][o][l]+=dp[i][j][k][o][l]*f[a[][l]][tmd];
continue;
}
if(t2==)
{
if(tag){
for(int t=;t<=num*;++t){
if(s2[]=='+')dp[i+][min(j+t,)][k][o][l]+=dp[i][j][k][o][l]*f[a[][l]][tmd]*f[num][t];
else dp[i+][max(j-t,)][k][o][l]+=dp[i][j][k][o][l]*f[a[][l]][tmd]*f[num][t];
}
}
else
{
if(s2[]=='+')dp[i+][min(j+num,)][k][o][l]+=dp[i][j][k][o][l]*f[a[][l]][tmd];
else dp[i+][max(j-num,)][k][o][l]+=dp[i][j][k][o][l]*f[a[][l]][tmd];
}
}
else if(t2==)
{
if(tag){
for(int t=;t<=num*;++t){
if(s2[]=='+')dp[i+][j][min(k+t,)][o][l]+=dp[i][j][k][o][l]*f[a[][l]][tmd]*f[num][t];
else dp[i+][j][max(k-t,)][o][l]+=dp[i][j][k][o][l]*f[a[][l]][tmd]*f[num][t];
}
}
else
{
if(s2[]=='+')dp[i+][j][min(k+num,)][o][l]+=dp[i][j][k][o][l]*f[a[][l]][tmd];
else dp[i+][j][max(k-num,)][o][l]+=dp[i][j][k][o][l]*f[a[][l]][tmd];
}
}
else if(t2==)
{
if(tag){
for(int t=;t<=num*;++t){
if(s2[]=='+')dp[i+][j][k][min(o+t,)][l]+=dp[i][j][k][o][l]*f[a[][l]][tmd]*f[num][t];
else dp[i+][j][k][max(o-t,)][l]+=dp[i][j][k][o][l]*f[a[][l]][tmd]*f[num][t];
}
}
else
{
if(s2[]=='+')dp[i+][j][k][min(o+num,)][l]+=dp[i][j][k][o][l]*f[a[][l]][tmd];
else dp[i+][j][k][max(o-num,)][l]+=dp[i][j][k][o][l]*f[a[][l]][tmd];
}
}
else
{
if(tag){
for(int t=;t<=num*;++t){
if(s2[]=='+')dp[i+][j][k][o][min(l+t,)]+=dp[i][j][k][o][l]*f[a[][l]][tmd]*f[num][t];
else dp[i+][j][k][o][max(l-t,)]+=dp[i][j][k][o][l]*f[a[][l]][tmd]*f[num][t];
}
}
else
{
if(s2[]=='+')dp[i+][j][k][o][min(l+num,)]+=dp[i][j][k][o][l]*f[a[][l]][tmd];
else dp[i+][j][k][o][max(l-num,)]+=dp[i][j][k][o][l]*f[a[][l]][tmd];
}
}
}
}
}
break;
}
case '>':
{
scanf("%d",&tg2);
if(l2==)--tg2;
scanf("%s%s",s1,s2+);
if(s1[]=='i')t2=;
else if(s1[]=='p')t2=;
else if(s1[]=='a')t2=;
else t2=; l2=strlen(s2+);
for(int j=;j<l2;++j)num=num*+s2[j]-'';
if(s2[l2]=='?')tag=;
else num=num*+s2[l2]-''; for(int j=;j<=;++j)
for(int k=;k<=;++k)
for(int o=;o<=;++o)
for(int l=;l<=;++l)
if(t1==)
{
for(int tmd=;tmd<=*a[][j];++tmd)
{
if(tmd<=tg2)
{
dp[i+][j][k][o][l]+=dp[i][j][k][o][l]*f[a[][j]][tmd];
continue;
}
if(t2==)
{
if(tag){
for(int t=;t<=num*;++t){
if(s2[]=='+')dp[i+][min(j+t,)][k][o][l]+=dp[i][j][k][o][l]*f[a[][j]][tmd]*f[num][t];
else dp[i+][max(j-t,)][k][o][l]+=dp[i][j][k][o][l]*f[a[][j]][tmd]*f[num][t];
}
}
else
{
if(s2[]=='+')dp[i+][min(j+num,)][k][o][l]+=dp[i][j][k][o][l]*f[a[][j]][tmd];
else dp[i+][max(j-num,)][k][o][l]+=dp[i][j][k][o][l]*f[a[][j]][tmd];
}
}
else if(t2==)
{
if(tag){
for(int t=;t<=num*;++t){
if(s2[]=='+')dp[i+][j][min(k+t,)][o][l]+=dp[i][j][k][o][l]*f[a[][j]][tmd]*f[num][t];
else dp[i+][j][max(k-t,)][o][l]+=dp[i][j][k][o][l]*f[a[][j]][tmd]*f[num][t];
}
}
else
{
if(s2[]=='+')dp[i+][j][min(k+num,)][o][l]+=dp[i][j][k][o][l]*f[a[][j]][tmd];
else dp[i+][j][max(k-num,)][o][l]+=dp[i][j][k][o][l]*f[a[][j]][tmd];
}
}
else if(t2==)
{
if(tag){
for(int t=;t<=num*;++t){
if(s2[]=='+')dp[i+][j][k][min(o+t,)][l]+=dp[i][j][k][o][l]*f[a[][j]][tmd]*f[num][t];
else dp[i+][j][k][max(o-t,)][l]+=dp[i][j][k][o][l]*f[a[][j]][tmd]*f[num][t];
}
}
else
{
if(s2[]=='+')dp[i+][j][k][min(o+num,)][l]+=dp[i][j][k][o][l]*f[a[][j]][tmd];
else dp[i+][j][k][max(o-num,)][l]+=dp[i][j][k][o][l]*f[a[][j]][tmd];
}
}
else
{
if(tag){
for(int t=;t<=num*;++t){
if(s2[]=='+')dp[i+][j][k][o][min(l+t,)]+=dp[i][j][k][o][l]*f[a[][j]][tmd]*f[num][t];
else dp[i+][j][k][o][max(l-t,)]+=dp[i][j][k][o][l]*f[a[][j]][tmd]*f[num][t];
}
}
else
{
if(s2[]=='+')dp[i+][j][k][o][min(l+num,)]+=dp[i][j][k][o][l]*f[a[][j]][tmd];
else dp[i+][j][k][o][max(l-num,)]+=dp[i][j][k][o][l]*f[a[][j]][tmd];
}
}
}
}
else if(t1==)
{
for(int tmd=;tmd<=*a[][k];++tmd)
{
if(tmd<=tg2)
{
dp[i+][j][k][o][l]+=dp[i][j][k][o][l]*f[a[][k]][tmd];
continue;
}
if(t2==)
{
if(tag){
for(int t=;t<=num*;++t){
if(s2[]=='+')dp[i+][min(j+t,)][k][o][l]+=dp[i][j][k][o][l]*f[a[][k]][tmd]*f[num][t];
else dp[i+][max(j-t,)][k][o][l]+=dp[i][j][k][o][l]*f[a[][k]][tmd]*f[num][t];
}
}
else
{
if(s2[]=='+')dp[i+][min(j+num,)][k][o][l]+=dp[i][j][k][o][l]*f[a[][k]][tmd];
else dp[i+][max(j-num,)][k][o][l]+=dp[i][j][k][o][l]*f[a[][k]][tmd];
}
}
else if(t2==)
{
if(tag){
for(int t=;t<=num*;++t){
if(s2[]=='+')dp[i+][j][min(k+t,)][o][l]+=dp[i][j][k][o][l]*f[a[][k]][tmd]*f[num][t];
else dp[i+][j][max(k-t,)][o][l]+=dp[i][j][k][o][l]*f[a[][k]][tmd]*f[num][t];
}
}
else
{
if(s2[]=='+')dp[i+][j][min(k+num,)][o][l]+=dp[i][j][k][o][l]*f[a[][k]][tmd];
else dp[i+][j][max(k-num,)][o][l]+=dp[i][j][k][o][l]*f[a[][k]][tmd];
}
}
else if(t2==)
{
if(tag){
for(int t=;t<=num*;++t){
if(s2[]=='+')dp[i+][j][k][min(o+t,)][l]+=dp[i][j][k][o][l]*f[a[][k]][tmd]*f[num][t];
else dp[i+][j][k][max(o-t,)][l]+=dp[i][j][k][o][l]*f[a[][k]][tmd]*f[num][t];
}
}
else
{
if(s2[]=='+')dp[i+][j][k][min(o+num,)][l]+=dp[i][j][k][o][l]*f[a[][k]][tmd];
else dp[i+][j][k][max(o-num,)][l]+=dp[i][j][k][o][l]*f[a[][k]][tmd];
}
}
else
{
if(tag){
for(int t=;t<=num*;++t){
if(s2[]=='+')dp[i+][j][k][o][min(l+t,)]+=dp[i][j][k][o][l]*f[a[][k]][tmd]*f[num][t];
else dp[i+][j][k][o][max(l-t,)]+=dp[i][j][k][o][l]*f[a[][k]][tmd]*f[num][t];
}
}
else
{
if(s2[]=='+')dp[i+][j][k][o][min(l+num,)]+=dp[i][j][k][o][l]*f[a[][k]][tmd];
else dp[i+][j][k][o][max(l-num,)]+=dp[i][j][k][o][l]*f[a[][k]][tmd];
}
}
}
}
else if(t1==)
{
for(int tmd=;tmd<=*a[][o];++tmd)
{
if(tmd<=tg2)
{
dp[i+][j][k][o][l]+=dp[i][j][k][o][l]*f[a[][o]][tmd];
continue;
}
if(t2==)
{
if(tag){
for(int t=;t<=num*;++t){
if(s2[]=='+')dp[i+][min(j+t,)][k][o][l]+=dp[i][j][k][o][l]*f[a[][o]][tmd]*f[num][t];
else dp[i+][max(j-t,)][k][o][l]+=dp[i][j][k][o][l]*f[a[][o]][tmd]*f[num][t];
}
}
else
{
if(s2[]=='+')dp[i+][min(j+num,)][k][o][l]+=dp[i][j][k][o][l]*f[a[][o]][tmd];
else dp[i+][max(j-num,)][k][o][l]+=dp[i][j][k][o][l]*f[a[][o]][tmd];
}
}
else if(t2==)
{
if(tag){
for(int t=;t<=num*;++t){
if(s2[]=='+')dp[i+][j][min(k+t,)][o][l]+=dp[i][j][k][o][l]*f[a[][o]][tmd]*f[num][t];
else dp[i+][j][max(k-t,)][o][l]+=dp[i][j][k][o][l]*f[a[][o]][tmd]*f[num][t];
}
}
else
{
if(s2[]=='+')dp[i+][j][min(k+num,)][o][l]+=dp[i][j][k][o][l]*f[a[][o]][tmd];
else dp[i+][j][max(k-num,)][o][l]+=dp[i][j][k][o][l]*f[a[][o]][tmd];
}
}
else if(t2==)
{
if(tag){
for(int t=;t<=num*;++t){
if(s2[]=='+')dp[i+][j][k][min(o+t,)][l]+=dp[i][j][k][o][l]*f[a[][o]][tmd]*f[num][t];
else dp[i+][j][k][max(o-t,)][l]+=dp[i][j][k][o][l]*f[a[][o]][tmd]*f[num][t];
}
}
else
{
if(s2[]=='+')dp[i+][j][k][min(o+num,)][l]+=dp[i][j][k][o][l]*f[a[][o]][tmd];
else dp[i+][j][k][max(o-num,)][l]+=dp[i][j][k][o][l]*f[a[][o]][tmd];
}
}
else
{ if(tag){
for(int t=;t<=num*;++t){
if(s2[]=='+')dp[i+][j][k][o][min(l+t,)]+=dp[i][j][k][o][l]*f[a[][o]][tmd]*f[num][t];
else dp[i+][j][k][o][max(l-t,)]+=dp[i][j][k][o][l]*f[a[][o]][tmd]*f[num][t];
}
}
else
{
if(s2[]=='+')dp[i+][j][k][o][min(l+num,)]+=dp[i][j][k][o][l]*f[a[][o]][tmd];
else dp[i+][j][k][o][max(l-num,)]+=dp[i][j][k][o][l]*f[a[][o]][tmd];
}
}
}
}
else
{
for(int tmd=;tmd<=*a[][l];++tmd)
{
if(tmd<=tg2)
{
dp[i+][j][k][o][l]+=dp[i][j][k][o][l]*f[a[][l]][tmd];
continue;
}
if(t2==)
{
if(tag){
for(int t=;t<=num*;++t){
if(s2[]=='+')dp[i+][min(j+t,)][k][o][l]+=dp[i][j][k][o][l]*f[a[][l]][tmd]*f[num][t];
else dp[i+][max(j-t,)][k][o][l]+=dp[i][j][k][o][l]*f[a[][l]][tmd]*f[num][t];
}
}
else
{
if(s2[]=='+')dp[i+][min(j+num,)][k][o][l]+=dp[i][j][k][o][l]*f[a[][l]][tmd];
else dp[i+][max(j-num,)][k][o][l]+=dp[i][j][k][o][l]*f[a[][l]][tmd];
}
}
else if(t2==)
{
if(tag){
for(int t=;t<=num*;++t){
if(s2[]=='+')dp[i+][j][min(k+t,)][o][l]+=dp[i][j][k][o][l]*f[a[][l]][tmd]*f[num][t];
else dp[i+][j][max(k-t,)][o][l]+=dp[i][j][k][o][l]*f[a[][l]][tmd]*f[num][t];
}
}
else
{
if(s2[]=='+')dp[i+][j][min(k+num,)][o][l]+=dp[i][j][k][o][l]*f[a[][l]][tmd];
else dp[i+][j][max(k-num,)][o][l]+=dp[i][j][k][o][l]*f[a[][l]][tmd];
}
}
else if(t2==)
{
if(tag){
for(int t=;t<=num*;++t){
if(s2[]=='+')dp[i+][j][k][min(o+t,)][l]+=dp[i][j][k][o][l]*f[a[][l]][tmd]*f[num][t];
else dp[i+][j][k][max(o-t,)][l]+=dp[i][j][k][o][l]*f[a[][l]][tmd]*f[num][t];
}
}
else
{
if(s2[]=='+')dp[i+][j][k][min(o+num,)][l]+=dp[i][j][k][o][l]*f[a[][l]][tmd];
else dp[i+][j][k][max(o-num,)][l]+=dp[i][j][k][o][l]*f[a[][l]][tmd];
}
}
else
{
if(tag){
for(int t=;t<=num*;++t){
if(s2[]=='+')dp[i+][j][k][o][min(l+t,)]+=dp[i][j][k][o][l]*f[a[][l]][tmd]*f[num][t];
else dp[i+][j][k][o][max(l-t,)]+=dp[i][j][k][o][l]*f[a[][l]][tmd]*f[num][t];
}
}
else
{
if(s2[]=='+')dp[i+][j][k][o][min(l+num,)]+=dp[i][j][k][o][l]*f[a[][l]][tmd];
else dp[i+][j][k][o][max(l-num,)]+=dp[i][j][k][o][l]*f[a[][l]][tmd];
}
}
}
}
break;
}
case '+':
{
for(int j=;j<l2;++j)num=num*+s2[j]-'';
if(s2[l2]=='?')tag=;
else num=num*+s2[l2]-'';
work1(t1,i,num,tag);
break;
}
case '-':
{
for(int j=;j<l2;++j)num=num*+s2[j]-'';
if(s2[l2]=='?')tag=;
else num=num*+s2[l2]-'';
work2(t1,i,num,tag);
break;
}
}
}
prans(n+);
}
40K超清代码
T3，dp or 记搜，考场上像一个sb一样打了状压，其实值域只有0，1，2，3。记录每一种有多少个以及上一次的操作即可。注意打高精
#include<iostream>
#include<cstdio>
#include<cstring>
#include<algorithm>
#include<vector>
#define N 13
using namespace std;
int n,a[N],sta;
int bk[N];
struct Big_int{
int a[];
inline void init(int x){while(x){a[++a[]]=x%;x/=;}}
inline bool empty(){return !a[];} inline void print()
{
for(int i=a[];i;--i)printf("%d",a[i]);
puts("");
}
}dp[][N][N][N][];
inline void add( Big_int &c,const Big_int &x,const int y)
{
if(!y)return;
c.a[]=max(c.a[],x.a[]);int t=;
for(int i=;i<=c.a[];++i){
c.a[i]+=x.a[i]*y+t;
t=c.a[i]/;c.a[i]%=;
}
while(t)c.a[++c.a[]]=t%,t/=;
return;
}
inline void work2()
{
int al=,cnt=;
for(int i=;i<=n;++i)al+=a[i];
dp[][bk[]][bk[]+][bk[]-][].init(bk[]);
dp[][bk[]+][bk[]-][bk[]][].init(bk[]);
dp[][bk[]-][bk[]][bk[]][].init(bk[]);
for(int o=;o<al;++o)
for(int i=;i<=n;++i)
for(int j=;j<=n;++j)
for(int k=;k<=n;++k)
for(int p=;p<=;++p){
if(dp[o][i][j][k][p].empty())continue;
// printf("dp[%d][%d][%d][%d][%d]=",o,i,j,k,p);dp[o][i][j][k][p].print();
if(k)add(dp[o+][i][j+][k-][],dp[o][i][j][k][p],k);
if(j)add(dp[o+][i+][j-][k][],dp[o][i][j][k][p],j-(p==));
if(i)add(dp[o+][i-][j][k][],dp[o][i][j][k][p],i-(p==));
}
dp[al][][][][].print();
}
int main()
{
cin>>n;
for(int i=;i<=n;++i)cin>>a[i],++bk[a[i]];
work2();return ;
}
模拟89。
T1，正解为图论，然而被各种乱搞*爆，%%%cbx大神打表发现用2，3，5，7筛即可。
#include<iostream>
#include<cstdio>
#include<cstring>
#include<vector>
#include<algorithm>
#define N 1000050
using namespace std;
int ans[N];
int n;
bool zhi[N];
int pri[N],tot;
inline int Min(int x,int y){if(x>y)return y;return x;}
int main()
{
// freopen("da.in","r",stdin);
// freopen("my.out","w",stdout);
ans[]=;ans[]=;
for(int i=;i<=;++i)ans[i]=i;
for(int i=;i<=;++i){
for(int j=i+;j<=i+;++j)ans[i]=Min(ans[i],ans[j]+j-i);
if(!zhi[i])pri[++tot]=i;
for(int j=;j<=tot&&1ll*i*pri[j]<=;++j)
{
ans[i*pri[j]]=Min(ans[i*pri[j]],ans[i]+pri[j]);
zhi[i*pri[j]]=;
}
}
scanf("%d",&n);
printf("%d\n",ans[n]);
return ;
}
本代码各种玄学操作均可用打表or枚举证明
T2，杜教筛and整除分块，考场上打线筛莫比乌斯能拿到40。
#include<bits/stdc++.h>
#define N 30000500
using namespace std;
long long n,ans;
bool zhi[N];
int pri[N],tot;
char mu[N];
int sum[N];
unordered_map<int,int>H;
inline void init(int n)
{
mu[]=sum[]=;
for(int i=;i<=n;++i){
if(!zhi[i])pri[++tot]=i,mu[i]=-;
sum[i]=sum[i-]+mu[i];
for(int j=;j<=tot&&1ll*i*pri[j]<=n;++j)
{
zhi[i*pri[j]]=;
if(i%pri[j])mu[i*pri[j]]=-mu[i];
else {mu[i*pri[j]]=;break;}
}
}
}
inline int getsm(int x)
{
if(x<=)return sum[x];
if(H.find(x)!=H.end())return H[x];
int ret=;
for(int l=,r;l<=x;l=r+)
{
r=x/(x/l);
ret-=getsm(x/l)*(r-l+);
}
return H[x]=ret;
}
inline void fenkuai()
{
int p=sqrt(n);
for(int l=,r;l<=p;l=r+){
r=sqrt(n/(n/l/l));
ans+=(getsm(r)-getsm(l-))*(n/l/l);
}
}
int main()
{
cin>>n;ans=n;
init();
fenkuai();
cout<<ans<<endl;
return ;
}
T3，正解为线段树维护单调栈，按题意模拟打treap可以拿到60（然而考场上删除函数打炸了，只有15分）
#include<bits/stdc++.h>
#define N 200050
using namespace std;
int n,m,A,lim,w;
int lsh[N];
int a[N];
struct node{int op,x,y;}q[N];
inline int py(int x){return A-x+;}
struct Segment_tree{
int ma[N<<],len[N<<],mi[N<<],po[N<<];
void build(int g,int l,int r)
{
len[g]=r-l+;
if(l==r)return;
const int m=l+r>>;
build(g<<,l,m);build(g<<|,m+,r);
}
inline void upd(int g)
{
if(ma[g<<]>ma[g<<|]){ma[g]=ma[g<<];po[g]=po[g<<];}
else{ma[g]=ma[g<<|];po[g]=po[g<<|];}mi[g]=mi[g<<];
}
inline int ask(int g,int l,int r)
{
if(ma[g]<=w||r<=lim)return ;
if(l>lim)
{
if(mi[g]>w){w=ma[g];return len[g];}
const int m=l+r>>;
if(ma[g<<]>w){
int ret=ask(g<<,l,m);if(ma[g<<|]>ma[g<<])w=ma[g<<|];
return ret+len[g]-len[g<<];
}
else return ask(g<<|,m+,r);
}
const int m=l+r>>;
if(m<=lim){return ask(g<<|,m+,r);}
else{
if(ma[g<<]<=w)return ask(g<<|,m+,r);
int ret=ask(g<<,l,m);
if(w==ma[g<<]){
if(ma[g<<|]>ma[g<<])w=ma[g<<|];
return ret+len[g]-len[g<<];
}
else{return ret+ask(g<<|,m+,r);}
}
}
inline int getma(int g,int l,int r,int x,int y)
{
if(l>y||r<x)return ;
if(l>=x&&r<=y)return po[g];
const int m=l+r>>;
const int a1=getma(g<<,l,m,x,y),a2=getma(g<<|,m+,r,x,y);
if(a[a1]>a[a2])return a1;return a2; }
void change(int g,int l,int r,int pos,int ww)
{
if(l==r){
mi[g]=ma[g]=ww;po[g]=l;
if(w){len[g]=,po[g]=l;}
else len[g]=po[g]=;
return;
}
const int m=l+r>>;
if(pos<=m)
{
change(g<<,l,m,pos,ww);upd(g);
lim=m;w=ma[g<<];
len[g]=len[g<<]+ask(g<<|,m+,r);
}
else
{
change(g<<|,m+,r,pos,ww);upd(g);
lim=m;w=ma[g<<];
len[g]=len[g<<]+ask(g<<|,m+,r);
}
}
}tr1,tr2;
inline void init(){
sort(lsh+,lsh+A+);
A=unique(lsh+,lsh+A+)-lsh-;
}
inline int getd(int x)
{
lim=x;w=a[x];
int ret=tr1.ask(,,A);
lim=py(x);w=a[x];
return ret+tr2.ask(,,A); }
int main()
{ scanf("%d",&n);
for(int i=;i<=n;++i)
{
scanf("%d",&q[i].op);
if(q[i].op==){
scanf("%d%d",&q[i].x,&q[i].y);
lsh[++A]=q[i].x;
}
else if(q[i].op==)scanf("%d",&q[i].x);
else scanf("%d%d",&q[i].x,&q[i].y);
}
init();
for(int i=,op,x,y,t;i<=n;++i)
{
// printf("\n\n\ni:%d\n",i);
op=q[i].op;
x=lower_bound(lsh+,lsh+A+,q[i].x)-lsh;
if(op==){
a[x]=q[i].y;
tr1.change(,,A,x,a[x]);
tr2.change(,,A,py(x),a[x]);
}
else if(q[i].op==)
{
a[x]=;
tr1.change(,,A,x,a[x]);
tr2.change(,,A,py(x),a[x]);
}
else
{
y=lower_bound(lsh+,lsh+A+,q[i].y)-lsh;
if(x>y)swap(x,y);t=tr1.getma(,,A,x,y);
printf("%d\n",getd(x)+getd(y)-*getd(t));
}
}
}
将坐标翻转减少码量
模拟90。
T1：luode dijkstra
#include<iostream>
#include<cstdio>
#include<cstring>
#include<algorithm>
#include<queue>
#define N 505
using namespace std;
const int dx[]={,-,,};
const int dy[]={,,,-};
int a[N][N],b[N][N],n,m;
int sx,sy,tx,ty;
priority_queue<pair<int,int> >q;
inline void bfs(int x,int y)
{
q.push(make_pair(b[sx][sy],x*N+y));
int d,xx,yy;
while(q.size())
{
x=q.top().second;d=q.top().first;q.pop();
y=x%N;x/=N;if(d!=b[x][y])continue;
for(int i=;i<=;++i)
{
xx=x+dx[i];yy=y+dy[i];
if(xx<=||xx>n||yy<=||yy>m)continue;
if(d<=a[xx][yy]+b[xx][yy])continue;
b[xx][yy]=d-a[xx][yy];
q.push(make_pair(b[xx][yy],xx*N+yy));
}
}
}
inline void pr()
{
for(int i=;i<=n;++i)
{
for(int j=;j<=m;++j)
{
printf("%d ",b[i][j]);
}
puts("");
}
}
int main()
{
scanf("%d%d",&n,&m);
for(int i=;i<=n;++i)
for(int j=;j<=m;++j)
scanf("%d",&a[i][j]);
scanf("%d%d",&sx,&sy);
scanf("%d%d%d",&b[sx][sy],&tx,&ty);
bfs(sx,sy);
printf("%d\n",b[tx][ty]);
// pr();
}
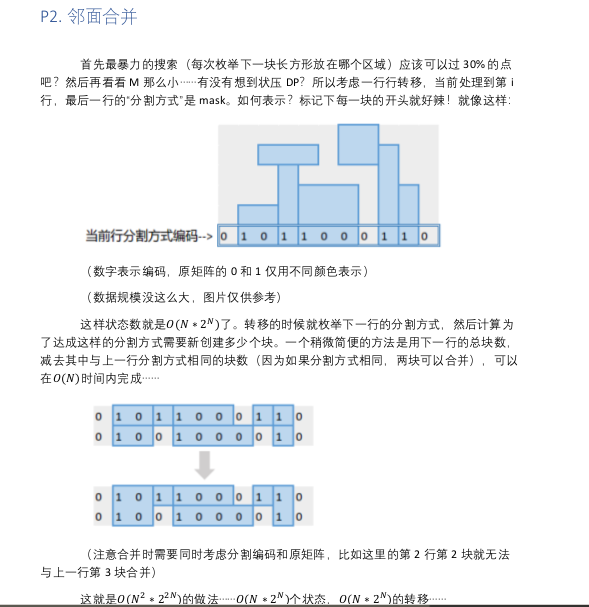
T2：状压dp，怎么压都行，然而考场上打sb了，WA30，kuku。。
题解状压的思路还是不错的，积累一下。
#include<iostream>
#include<cstdio>
#include<cstring>
#include<algorithm>
#include<queue>
#define N 105
using namespace std;
const int inf=;
int n,m,bin[],dp[N][<<],ct[<<],sta[N],ans=inf;
inline void init(int n)
{
for(int i=;i<=bin[n];++i)
ct[i]=ct[i-(i&-i)]+;
}
int main()
{
for(int i=;i<=;++i)bin[i]=<<i;
memset(dp,0x3f,sizeof(dp));
scanf("%d%d",&n,&m);
for(int i=;i<=n;++i)
for(int j=,x;j<m;++j){
scanf("%d",&x);
if(x)sta[i]|=bin[j];
}
init(m);dp[][]=;
for(int j=;j<n;++j)
{
for(int i=,cnt,ok;i<bin[m];++i)
{
if(dp[j][i]>=inf)continue;
if(!sta[j+]){dp[j+][]=min(dp[j+][],dp[j][i]);continue;}
for(int st=sta[j+],ok;st;st=(st-)&sta[j+]){
ok=;cnt=ct[st];
if((sta[j+]&bin[])&&!(st&bin[]))continue;
for(int k=;k<m-;++k){
if(sta[j+]&bin[k])continue;
if((sta[j+]&bin[k+])&&!(st&bin[k+])){ok=;break;}
}
if(!ok)continue;
for(int k=,s1,s2;k<m;++k){
if((i&bin[k])&&(st&bin[k]))
{
for(s1=k+;s1<m;++s1)if(!(sta[j]&bin[s1])||(i&bin[s1]))break;
for(s2=k+;s2<m;++s2)if(!(sta[j+]&bin[s2])||(st&bin[s2]))break;
if(s1==s2)--cnt;
}
}
dp[j+][st]=min(dp[j+][st],dp[j][i]+cnt);
}
}
}
for(int i=,cnt,ok;i<bin[m];++i)ans=min(ans,dp[n][i]);
printf("%d\n",ans);
}
T3：%%%kx
对所有斜率进行离散化，对矩形的左边界和下边界分别维护一棵线段树，下标为斜率离散化后的下标。然后标记永久化一下就可以了。
注意各种各样的特判（y==0和x==0）。
#include<bits/stdc++.h>
#define N 100050
using namespace std;
int n,m,ls;
const double eps=1e-;
const int inf=;
double lsh[N<<];
struct PA{
double first;
int second;
friend bool operator <(const PA &a,const PA &b)
{
if(a.first==b.first)return a.second<b.second;
return a.first<b.first;
}
};
inline PA mmp(int x,int y){PA a;a.first=x;a.second=y;return a;}
PA kkk;
struct node{double x,xx,y,yy;int op;}q[N];
struct Segment_tree{
PA mi[N<<];
inline void build(int g,int l,int r)
{
mi[g]=mmp(inf,);if(l==r)return;
const int m=l+r>>;
build(g<<,l,m);build(g<<|,m+,r);
}
inline PA getmi(int g,int l,int r,int pos)
{
if(l==r)return mi[g];
const int m=l+r>>;
PA ret;
if(pos<=m)ret=getmi(g<<,l,m,pos);
else ret=getmi(g<<|,m+,r,pos);
return min(ret,mi[g]);
}
inline void add(int g,int l,int r,int x,int y)
{
if(l>y||r<x)return;
if(l>=x&&r<=y){mi[g]=min(mi[g],kkk);return;}
const int m=l+r>>;
add(g<<,l,m,x,y);add(g<<|,m+,r,x,y);
}
}T1,T2;
int main(){
scanf("%d",&n);
for(int i=;i<=n;++i)
{
scanf("%d",&q[i].op);
if(q[i].op==){
scanf("%lf%lf%lf%lf",&q[i].x,&q[i].y,&q[i].xx,&q[i].yy);
if(q[i].x)lsh[++ls]=q[i].y/q[i].x,lsh[++ls]=q[i].yy/q[i].x;
if(q[i].xx)lsh[++ls]=q[i].y/q[i].xx;
}
else{
scanf("%lf%lf",&q[i].x,&q[i].y);
if(q[i].x)lsh[++ls]=q[i].y/q[i].x;
}
}
sort(lsh+,lsh+ls+);ls=unique(lsh+,lsh+ls+)-lsh-;
double x,y,xx,yy;int t1,t2;
PA k1,k2,spj=mmp(inf,),spj2=mmp(inf,);
T1.build(,,ls);T2.build(,,ls);
q[].x=inf;q[].y=inf;
for(int i=,op;i<=n;++i)
{
op=q[i].op;x=q[i].x;y=q[i].y;xx=q[i].xx;yy=q[i].yy;
if(op==)
{
kkk=mmp(x,-i);
if(!y)spj2=min(spj2,mmp(x,-i));
if(x)
{
t1=lower_bound(lsh+,lsh+ls+,y/x-eps)-lsh;
t2=lower_bound(lsh+,lsh+ls+,yy/x-eps)-lsh;
}
else
{
spj=min(spj,mmp(y,-i));
t1=t2=ls;
}
T1.add(,,ls,t1,t2);
kkk=mmp(y,-i);
if(xx)t2=lower_bound(lsh+,lsh+ls+,y/xx-eps)-lsh;
else t2=ls;
T2.add(,,ls,t2,t1);
}
else
{
if(!q[i].y){printf("%d\n",-spj2.second);continue;}
if(!q[i].x){printf("%d\n",-spj.second);continue;}
t1=lower_bound(lsh+,lsh+ls+,y/x-eps)-lsh;
k1=T1.getmi(,,ls,t1);k2=T2.getmi(,,ls,t1);
yy=max(q[-k1.second].x*y/x,q[-k1.second].y);xx=max(q[-k2.second].x*y/x,q[-k2.second].y);
if(fabs(yy-xx)<1e-){printf("%d\n",-min(k1.second,k2.second));}
else if(yy>xx)printf("%d\n",-k2.second);
else printf("%d\n",-k1.second);
}
}
}
模拟91。
T1，下面说一下心态问题，我当时秒切
发现不同的数在根号级别，然后它就成了sbt。开链表维护存在的权值，每次暴扫即可。
#include<iostream>
#include<cstdio>
#include<cstring>
#include<algorithm>
#define N 300050
using namespace std;
int n,m,tot;
int fa[N],sz[N];
int pd[N]; struct node{int pre,ne,cnt,sum;}a[N];
int getfa(int x){return x==fa[x]?x:fa[x]=getfa(fa[x]);} inline void del(int id)
{
pd[id]=;
a[a[id].pre].ne=a[id].ne;
a[a[id].ne].pre=a[id].pre;
}
inline void ins2(int x,int id)
{
a[x].pre=a[id].pre;
a[a[id].pre].ne=x;
a[id].pre=x;a[x].ne=id;
pd[x]=;
}
inline void ins(int x)
{
for(int i=a[].ne;i<=n+;i=a[i].ne)
if(i>x){ins2(x,i);return;}
} int main()
{
// freopen("cards105.in","r",stdin);//diff -b -B cards105.out my.out
// freopen("my.out","w",stdout);
scanf("%d%d",&n,&m);tot=;
for(int i=;i<=n;++i)fa[i]=i,sz[i]=; a[].ne=a[n+].pre=;
a[].pre=;a[].ne=n+;
a[].cnt=n;pd[]=; int op,x,y,sum;
long long ans;
while(m--)
{
scanf("%d",&op);
if(op==)
{
scanf("%d%d",&x,&y);
if(getfa(x)==getfa(y))continue;
x=getfa(x);y=getfa(y);
--a[sz[x]].cnt;
if(!a[sz[x]].cnt)del(sz[x]);
--a[sz[y]].cnt;
if(!a[sz[y]].cnt)del(sz[y]); fa[y]=x;sz[x]+=sz[y];
++a[sz[x]].cnt;
if(!pd[sz[x]])ins(sz[x]);
}
else
{
scanf("%d",&x);
for(int i=a[].ne;i<=n;i=a[i].ne)
{
a[i].sum=a[i].cnt+a[a[i].pre].sum;
}
ans=;
if(!x){
ans=1ll*a[a[n+].pre].sum*(a[a[n+].pre].sum-);ans>>=;
}
else
{
for(int i=a[n+].pre,j=a[n+].pre;i>x;i=a[i].pre)
{
while(i-j<x)j=a[j].pre;
ans+=1ll*a[j].sum*a[i].cnt;
}
}
printf("%lld\n",ans);
}
}
}
竟然花了我一个小时？？？
T2，考场上大部分时间都扔给了T2，然而还是爆0了。
其实还是挺难的，考虑按概率dp，最后用概率乘位置得到期望。
考虑如何归并相同的数。
设dp[dep][i][j]，表示在归并的第dep层，原数组中位置为i的值在当前归并的区间内排名为j的概率，在l==r时显然有dp[dep][l][1]=1。
对于非叶子
首先，已有两个子区间各自的排名，考虑预处理一些东西辅助转移。
设f[i][j]表示某点在原区间排名为j，在新区间排名为i的概率，
f数组可以递推转移（考虑前一个位置来自相同区间or不同区间，具体细节看代码）
但我们发现只有一个f数组还不够。因为不能确定另一个子区间是否已为空
设h[i][j]表示某点在原区间排名为j，在新区间排名为i，且另一个子区间的数全部在当前数之前的概率。
转移与f数组类似（同样考虑前一个位置来自相同区间or不同区间，具体细节看代码）
然后就可以kx地转移了。
#include<bits/stdc++.h>
#define N 550
#define pb push_back
#define int long long
const int mod=;
const int inv2=;
using namespace std;
int n,a[N],dp[][N][N],f[N][N],h[N][N],pd[],ans[N];
vector<int>v[N<<];
inline void init(int n)
{
f[][]=inv2;h[][]=;
for(int i=;i<=n;++i)
for(int j=;j<=i;++j){
f[i][j]=(f[i-][j-]+f[i-][i-j])%mod;
f[i][j]=1ll*inv2*f[i][j]%mod;
h[i][j]=(h[i-][j-]+f[i-][i-j])%mod;
}
}
inline void merge(int g,int l,int r,int dep,int val)
{
v[g].clear();
if(l==r){if(a[l]==val)dp[dep][l][]=,v[g].pb(l);return;}
const int m=l+r>>,lc=g<<,rc=g<<|;;
merge(lc,l,m,dep+,val);merge(rc,m+,r,dep+,val);
for(int i=;i<v[lc].size();++i)v[g].pb(v[lc][i]);
for(int j=;j<v[rc].size();++j)v[g].pb(v[rc][j]);
for(int o=,t;o<v[lc].size();++o){t=v[lc][o];
for(int i=;i<=v[lc].size();++i)
for(int j=;j<=v[rc].size();++j)
if(j==v[rc].size())(dp[dep][t][i+j]+=1ll*dp[dep+][t][i]*h[i+j][i]%mod)%=mod;
else (dp[dep][t][i+j]+=1ll*dp[dep+][t][i]*f[i+j][i]%mod)%=mod;
}
for(int o=,t;o<v[rc].size();++o){t=v[rc][o];
for(int i=;i<=v[rc].size();++i)
for(int j=;j<=v[lc].size();++j)
if(j==v[lc].size())(dp[dep][t][i+j]+=1ll*dp[dep+][t][i]*h[i+j][i]%mod)%=mod;
else (dp[dep][t][i+j]+=dp[dep+][t][i]*f[i+j][i]%mod)%=mod;
}
v[lc].clear();v[rc].clear();
}
signed main()
{
scanf("%lld",&n);init(n);
for(int i=;i<=n;++i)scanf("%lld",&a[i]);
for(int i=;i<=n;++i)
if(!pd[a[i]])pd[a[i]]=,merge(,,n,,a[i]);
for(int k=;k<=;++k)v[k].clear();
for(int i=;i<=n;++i)v[a[i]].push_back(i);
for(int k=,t=;k<=;++k){
for(int i=,p;i<v[k].size();++i){p=v[k][i];
for(int j=;j<=v[k].size();++j)(ans[p]+=1ll*dp[][p][j]*(j+t-)%mod)%=mod;
}
t+=v[k].size();
}
for(int i=;i<=n;++i)printf("%lld ",ans[i]);
puts("");
}
#include<bits/stdc++.h>
#define N 550
#define pb push_back
const int mod=;
const double inv2=0.5;
using namespace std;
int n;
int a[N],b[N],c[N];
double dp[][N][N];
double f[N][N];
double h[N][N];
double ans[N];
vector<int>v[N<<];
inline void init(int n)
{
f[][]=inv2;h[][]=;
for(int i=;i<=n;++i){
for(int j=;j<=i;++j){
f[i][j]=f[i-][j-]+f[i-][i-j];
f[i][j]= inv2*f[i][j] ;
h[i][j]=( h[i-][j-]+ f[i-][i-j]);
}
}
// for(int i=1;i<=n;++i,puts(""))
// for(int j=1;j<=i;++j)printf("%.2lf ",f[i][j]);
}
int pd[];
inline void merge(int g,int l,int r,int dep,int val)
{
v[g].clear();
if(l==r){
if(a[l]==val){
dp[dep][l][]=;
v[g].pb(l);
}return;
}
const int m=l+r>>,lc=g<<,rc=g<<|;;
merge(lc,l,m,dep+,val);merge(rc,m+,r,dep+,val);
for(int i=;i<v[lc].size();++i)v[g].pb(v[lc][i]);
for(int j=;j<v[rc].size();++j)v[g].pb(v[rc][j]);
for(int o=,t;o<v[lc].size();++o){t=v[lc][o];
for(int i=;i<=v[lc].size();++i)
for(int j=;j<=v[rc].size();++j)
if(j==v[rc].size())dp[dep][t][i+j]+=dp[dep+][t][i]*h[i+j][i];
else dp[dep][t][i+j]+=dp[dep+][t][i]*f[i+j][i];
}
for(int o=,t;o<v[rc].size();++o){t=v[rc][o];
for(int i=;i<=v[rc].size();++i)
for(int j=;j<=v[lc].size();++j)
if(j==v[lc].size())dp[dep][t][i+j]+=dp[dep+][t][i]*h[i+j][i];
else dp[dep][t][i+j]+=dp[dep+][t][i]*f[i+j][i];
}v[lc].clear();v[rc].clear();
}
int main()
{
scanf("%d",&n);init(n);
for(int i=;i<=n;++i)scanf("%d",&a[i]),b[i]=a[i];
for(int i=;i<=n;++i){
if(!pd[a[i]]){pd[a[i]]=;
merge(,,n,,a[i]);
}
}
for(int k=;k<=;++k)v[k].clear();
for(int i=;i<=n;++i)v[a[i]].push_back(i);
int t=;
for(int k=;k<=;++k){
for(int i=,p;i<v[k].size();++i){p=v[k][i];
for(int j=;j<=v[k].size();++j)ans[p]+=dp[][p][j]*(j+t-);
}
t+=v[k].size();
}
for(int i=;i<=n;++i)printf("%lf ",ans[i]);
puts("");
}
double版本，调试专用
T3，直接粘题接&代码，此题给我的启示：学习暴力，学习卡常，++前置，加fread，重载max或直接用if，学会乱搞，减小枚举上界，然后就可以卡常AC此题
#include<bits/stdc++.h>
#define N 1000050
char xch,xB[<<],*xS=xB,*xTT=xB;
#define getc() (xS==xTT&&(xTT=(xS=xB)+fread(xB,1,1<<15,stdin),xS==xTT)?0:*xS++)
inline int read()
{
int x=,f=;char ch=getc();
while(ch<''|ch>''){if(ch=='-')f=-;ch=getc();}
while(ch>=''&&ch<=''){x=x*+ch-'';ch=getc();}
return x*f;
}
using namespace std;
int n,K;
int a[N];
int ans[N];
int an2[N];
inline void work1()
{
for(int i=;i<=n;++i)ans[i]=-;
int ma,mi,an,o;
for(int i=n;i>=;--i){
ma=mi=an=o=a[i];
for(int k=i+;k<=n;++k){
if(a[k]>ma)ma=a[k];
if(a[k]<mi)mi=a[k];
an&=a[k];o|=a[k];
if(o+mi-ma-an>=K)ans[i]=k-i+;
}
for(int k=min(n,i+ans[i]-);k>i;--k)if(ans[k]<ans[i])ans[k]=ans[i];
}
for(int i=;i<=n;++i)printf("%d ",ans[i]);
puts("");
}
inline void work2()
{
for(int i=;i<=n;++i)ans[i]=-;
int ma,mi,an,o;
for(int i=n;i>=;--i){
ma=mi=an=o=a[i];
const int lim=min(n,i+);
for(int k=i+;k<=lim;++k){
if(a[k]>ma)ma=a[k];
if(a[k]<mi)mi=a[k];
an&=a[k];o|=a[k];
if(o+mi-ma-an>=K)ans[i]=k-i+;
}
for(int k=min(n,i+ans[i]-);k>i;--k)if(ans[k]<ans[i])ans[k]=ans[i];
}
for(int i=;i<=n;++i)printf("%d ",ans[i]);
puts("");
}
int main()
{
scanf("%d%d",&n,&K);
for(int i=;i<=n;++i)a[i]=read();
if(n>){work2();return ;}
work1();return ;
}
底层优化，13365 ms
以下是正解：
正解代码：
#include<bits/stdc++.h>
#define N 1000050
char xch,xB[<<],*xS=xB,*xTT=xB;
#define getc() (xS==xTT&&(xTT=(xS=xB)+fread(xB,1,1<<15,stdin),xS==xTT)?0:*xS++)
inline int read()
{
int x=,f=;char ch=getc();
while(ch<''|ch>''){if(ch=='-')f=-;ch=getc();}
while(ch>=''&&ch<=''){x=x*+ch-'';ch=getc();}
return x*f;
}
using namespace std;
int n,K,a[N],ans[N],bin[],lg[N];
int st1[][N],st2[][N],st3[][N],st4[][N];//min max and or
inline void init()
{
for(int i=;i<=;++i)bin[i]=<<i;lg[]=;
for(int i=;i<=n;++i)lg[i]=lg[i>>]+;
for(int i=;i<=n;++i)st1[][i]=st2[][i]=st3[][i]=st4[][i]=a[i];
for(int j=;j<=;++j)
for(int i=;i<=n;++i){
st1[j][i]=min(st1[j-][i],st1[j-][i+bin[j-]]);
st2[j][i]=max(st2[j-][i],st2[j-][i+bin[j-]]);
st3[j][i]=st3[j-][i]&st3[j-][i+bin[j-]];
st4[j][i]=st4[j-][i]|st4[j-][i+bin[j-]];
}
}
inline int Min(int l,int r){return min(st1[lg[r-l+]][l],st1[lg[r-l+]][r-bin[lg[r-l+]]+]);}
inline int Max(int l,int r){return max(st2[lg[r-l+]][l],st2[lg[r-l+]][r-bin[lg[r-l+]]+]);}
inline int And(int l,int r){return st3[lg[r-l+]][l]&st3[lg[r-l+]][r-bin[lg[r-l+]]+];}
inline int Or(int l,int r){return st4[lg[r-l+]][l]|st4[lg[r-l+]][r-bin[lg[r-l+]]+];}
inline int getval(int l,int r){return Or(l,r)-And(l,r);}
struct list{int ne,pre,l,r;}li[N];int tot=,kkk;
inline void del(int id){
int a1=li[id].pre,a2=li[id].ne;
li[a1].ne=a2;li[a2].pre=a1;li[a2].l=li[id].l;
}
inline bool check(int l,int r){
// printf("you checked:%d %d returned :%d\n",l,r,Or(l,r)+Min(l,r)-And(l,r)-Max(l,r));
return Or(l,r)+Min(l,r)-And(l,r)-Max(l,r)>=K;
}
int ma[N<<];
inline void add(int g,int l,int r,int x,int y,int w){
if(l>y||r<x)return;
if(l>=x&&r<=y){ma[g]=max(ma[g],w);return;}
const int m=l+r>>;
add(g<<,l,m,x,y,w);add(g<<|,m+,r,x,y,w);
}
inline void bl(int g,int l,int r)
{
ma[g]=max(ma[g],ma[g>>]);
if(l==r){printf("%d ",ma[g]);return;}
const int m=l+r>>;
bl(g<<,l,m);bl(g<<|,m+,r);
}
inline void erfen(int l,int r,const int alr)
{
// printf("l:%d r:%d\n",l,r);
int mid;
while(l+<r)
{
mid=l+r>>;
if(check(mid,alr))r=mid;
else l=mid;
}
add(,,n,r,alr,alr-r+);
}
int main()
{
scanf("%d%d",&n,&K);memset(ma,0xFF,sizeof(ma));
for(int i=;i<=n;++i)a[i]=read();
init();li[].l=li[].r=;
for(int i=;i<=n;++i)
{
// printf("now:%d \n",i);
li[kkk].ne=++tot;li[tot].pre=kkk;kkk=tot;
li[kkk].l=li[kkk].r=i;
for(int j=li[kkk].pre;j;j=li[j].pre)
if(getval(li[j].l,i)==getval(li[li[j].ne].l,i))del(j);
for(int j=li[].ne;j;j=li[j].ne)
if(check(li[j].r,i)){erfen(li[j].l-,li[j].r,i);break;}
}
bl(,,n);
puts("");
}
链表维护，3263ms
革命尚未成功，吾辈仍需努力
CSPS模拟88-91的更多相关文章
- csp-s模拟测试91
csp-s模拟测试91 倒悬吃屎的一套题. $T1$认真(?)分析题意发现复杂度不能带$n$(?),计划直接维护答案,考虑操作对答案的影响,未果.突然发现可以动态开点权值线段树打部分分,后来$Tm$一 ...
- CSPS模拟 88
今天我还是个弟弟. 果然唯有AK不可超越.. T1 决策单调性,暴力上整体二分. 极限数据跑的挺快,可是被n<k的脑残测试点qj了.. T2 又是大模拟! T3 想到剩余同种数量的彩球完全等效 ...
- 2019.10.28 csp-s模拟测试91 反思总结
有一场没一场的233 T1: 胡乱分析一下题意,发现和为n的x个正整数,不同的数字种类不会超过√n个.假设这x个数字都不同,最多也就是(x+1)*x/2=n. 所以可以维护现有的size值以及对应的数 ...
- 反省——关于csp-s模拟50
本人于搜索csp-s模拟49题解时,有意识地点开了一篇关于csp-s模拟50T2的题解,并知道了题解是二维前缀和以及四维偏序. 更重要的是,那篇博客说有解法二,叫二维莫队. 于是我上网搜索二维莫队,结 ...
- csp-s模拟测试99
csp-s模拟测试99 九九归一直接爆炸. $T1$一眼板子. $T2$一眼语文题(语文的唯一一次$120+$是给模拟出来的可知我的语文能力). $T3$一眼普及题. ?? Hours Later 板 ...
- csp-s模拟测试98
csp-s模拟测试98 $T1$??不是我吹我轻松手玩20*20.$T2$装鸭好像挺可做?$T3$性质数据挺多提示很明显? $One$ $Hour$ $Later$ 这$T1$什么傻逼题真$jb$难调 ...
- csp-s模拟测试97
csp-s模拟测试97 猿型毕露.水题一眼秒,火题切不动,还是太菜了. $T1$看了一会儿感觉$woc$期望题$T1??$假的吧??. $T2$秒. $T3$什么玩意儿. 40 01:24:46 00 ...
- csp-s模拟测试96
csp-s模拟测试96 $T1$一眼慢速乘,$T2$稍证一手最优性尝试用神奇数据结构优化,无果,弃.$T3$暴力+信仰. 100 03:16:38 95 03:16:56 35 03:17:10 23 ...
- csp-s模拟测试95
csp-s模拟测试95 去世场祭. $T1$:这不裸的除法分块吗. $T2$:这不裸的数据结构优化$Dp$吗. $T3$:这不裸的我什么都不会搜索骗$30$分吗. 几分钟后. 这除法分块太劲了..(你 ...
随机推荐
- PowerBuilder学习笔记之行删除卡死问题
在数据窗口勾选这两个选项后,在删除行数据时会导致系统直接崩溃退出
- Vue基础语法(样式绑定,事件处理,表单,Vue组件)
样式绑定 事件处理 表单 Vue组件 样式绑定 <!DOCTYPE html> <html> <head> <meta charset="utf-8 ...
- 使用Spring Cloud OAuth2和JWT保护微服务
采用Spring Security AOuth2 和 JWT 的方式,避免每次请求都需要远程调度 Uaa 服务.采用Spring Security OAuth2 和 JWT 的方式,Uaa 服务只验证 ...
- ES与关系型数据库的通俗比较
1.在Elasticsearch中,文档归属于一种类型(type),而这些类型存在于索引(index)中,我们可以画一些简单的对比图来类比传统关系型数据库: Relational DB -> D ...
- .ajaxStart() / .ajaxStop() —— ajax请求开始时 / 结束时触发
一..ajaxStart()——ajax请求开始时触发 描述:ajax请求开始时触发 .ajaxStart()的回调函数,全局的,所有的ajax都可以用 写法:元素.ajaxStart(functi ...
- 解决Maven 编译出的jar中没有主清单属性
出现这个问题的原因是 pom 中没有添加主程序入口 在配置中添加如下配置 <plugin> <groupId>org.apache.maven.plugins</grou ...
- Docker 镜像 && 容器的基本操作
镜像 && 容器 docker 镜像好比操作系统的镜像(iso) docker 容器好比是已安装运行的操作系统 所以说 docker 镜像文件运行起来之后,就是我们所说的 docker ...
- 一、zuul如何路由到上游服务器
所有文章 https://www.cnblogs.com/lay2017/p/11908715.html 正文 zuul在分布式项目中充当着一个网关的角色,而它最主要的功能像nginx一样针对上游服务 ...
- 目标进程已退出，但未引发 CoreCLR 启动事件
目标进程已退出,但未引发 CoreCLR 启动事件.请确保将目标进程配置为使用 .NET Core.如果目标进程未运行 .NET Core,则发生这种情况并不意外 解决:更新SDK版本
- iOS - error：unrecognized selector sent to class 导入第三方SDK .a后不识别，运行崩溃
今天将app统计的.a静态库包含到一个app应用中,调试时报下面的错误: *** Terminating app due to uncaught exception 'NSInvalidArgumen ...