[学习笔记] Uplift Decision Tree With KL Divergence

Uplift Decision Tree With KL Divergence

Intro

Uplift model 我没找到一个合适的翻译，这方法主要应用是，探究用户在给予一定激励之后的表现，也就是在电商领域，比如我们给一部分用户发了一些优惠券，那么这些行为是否将“转化”用户呢？是否会起一些积极作用呢？Uplift Model是模拟增量操作对个人行为的影响的。（经济学的人研究）

而在决策树中，我们给一部分样本treatment，而不给另一部分样本treatment，这样相当于每个样本都多了一个属性，也就是是否被给予treatment，利用这一点，我们可以计算给予treatment和未被给予treatment的样本的KL散度，然后每次节点分裂使得KL散度最大化，这样可以使得给予treatment和未被给予treatment的样本距离最远。因此，使用KL散度来做节点分裂距离的思想就是使得分裂前后子节点的平均KL散度增加，而且相对父节点最大增加。

KL-Divergence

KL散度在学习分类问题的交叉熵的时候非常常见，从概率论角度，KL散度的本质是衡量两个分布的距离，从信息论角度，他的本质是使用p分布来编码q所需要的编码长度。

KL散度的数学定义为:
\[
KL(P:Q) = \sum_i p_i log(\frac{p_i}{q_i})
\]

Uplift Decision Tree

首先定义分裂前后treatment和没给treatment的数据的KL散度：

分裂前两者的KL散度为：(其中C表示没给treatment)
\[
KL(P^T(Y):P^C(Y)) = \sum_i p^T(y_i) log\frac{p^T(y_i)}{p^C(y_i)}
\]
以A属性作为分裂属性分裂后的条件KL散度：(a代表属性取值，N代表分裂之前总样本数，N(a)是该属性取该值的样本数)
\[
KL((P^T(Y):P^C(Y))|A) = \sum_{a}\frac{N(a)}{N}D(P^T(Y|a):P^C(Y|a))
\]
则最终KL散度的增量为：
\[
KL_{gain} = KL((P^T(Y):P^C(Y))|A) - KL(P^T(Y):P^C(Y))
\]
计算每个属性分裂属性

最终求得最大的作为分裂的标准。

Example

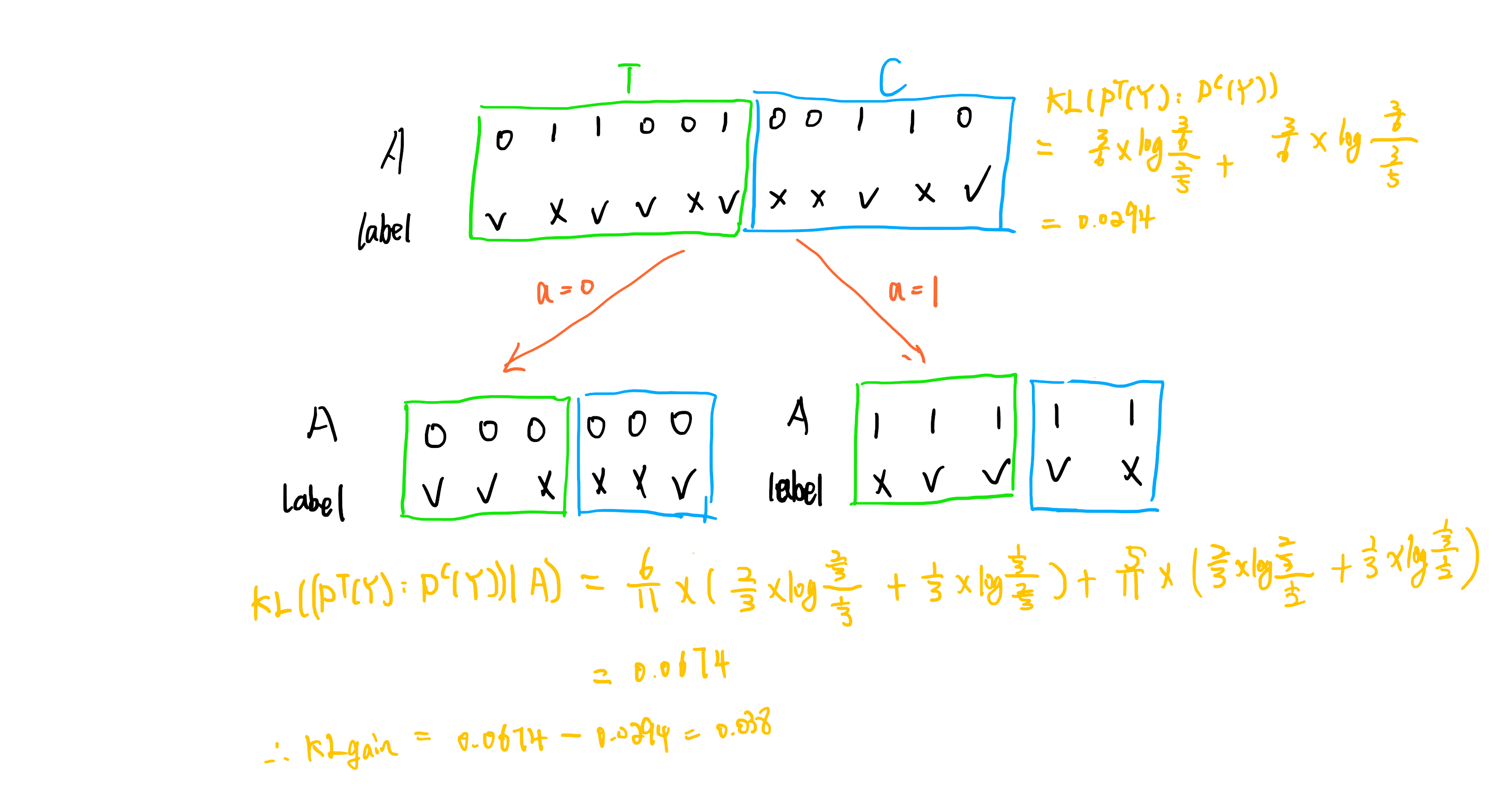
Coding

import numpy as np
import random
class Node():
    def __init__(self):
        self.children = []
        self.value = None
        self.attr = None
        self.attr_values = []
class DecistionTree():
    def __init__(self,dataset,attrs,mode = "Entropy"):
        self.dataset = np.array(dataset)
        self.attrs = attrs
        self.root = Node()
        self.mode = mode
    def predict(self,sample,root):
        attr = root.attr # 属性名
        res = ""
        #print("****start at attribute:{}****".format(attr))
        attr_idx = self.attrs.index(attr) # 这个属性的idx
        flag = False
        if sample[0,attr_idx] in root.attr_values:
            index = root.attr_values.index(sample[0,attr_idx]) # 本节点的属性对应的第几个子节点，也就是子节点index
            value = root.children[index].value
            #print(type(value))
            if type(value) is np.str_:
                #print(value)
                res = value
            else:
                res = self.predict(sample,root.children[index])

        return res
    def create_tree(self,dataset,attrs,root):
        label = dataset[:,-1]

        if len(set(list(label))) == 1:
            return label[0]
        #if dataset.shape[1] == 2: # 全部遍历完了
        #    return label[0]
        if len(attrs) == 0:
            return label[0]
        idx = self.chooseBestFeatureToSplit(dataset) # feature idx
        myTree = []
        myTree.append(self.attrs[attrs[idx]])
        root.attr = self.attrs[attrs[idx]]
        attrs.remove(attrs[idx])

        #root.childen.append(idx)
        values = set(list(dataset[:,idx]))

        for value in values:
            sub_dataset = dataset[dataset[:,idx] == value]
            new_node = Node()
            sub_dataset = np.delete(sub_dataset,idx,axis = 1)
            sub_tree = self.create_tree(sub_dataset[:],attrs,new_node)
            #print(sub_tree,type(sub_tree))
            if type(sub_tree) is np.str_:

                new_node.value = sub_tree
            root.children.append(new_node)
            root.attr_values.append(value)

            myTree.append(sub_tree)
        return root
        #return myTree
    def train(self,attrs):
        tree = self.create_tree(self.dataset,attrs,self.root)
        #print(tree)
        #print(self.root.attr,self.root.attr_values)
        #print(['age', ['prescript', ['astigmatic', 'nolenses', ['tearRate', 'soft', 'nolenses']], 'nolenses'], 'nolenses', 'nolenses'])
    def random_chosen(self,ratio = 0.5):
        assert ratio < 1 and ratio > 0.1
        idx = np.arange(self.dataset.shape[0]) # 样本个数
        choice = random.choices(idx,k = int(len(idx) * ratio)) # 正样本idx
        converted = np.zeros(shape = (len(idx),))
        converted[choice] = 1
        self.dataset = np.insert(self.dataset,-1,converted,axis = 1)
    @staticmethod
    def KL_divergence(sub_dataset):
        dataset1 = sub_dataset[sub_dataset[:,-2] == '1.0']
        dataset2 = sub_dataset[sub_dataset[:,-2] == '0.0']
        labels = set(list(sub_dataset[:,-1]))
        num_dataset1,num_dataset2 = dataset1.shape[0],dataset2.shape[0]
        res = 0.
        for label in labels:

            p = np.mean(dataset1[:,-1] == label)
            q = np.mean(dataset2[:,-1] == label) + 1e-5
            if p >0:
                res += (p* np.log2(p/q))
        return res
    @staticmethod
    def Entropy(dataSet):
        dataSet = np.array(dataSet)
        labels = dataSet[:,-1]
        label_set = list(set(list(labels)))
        num_classes = len(label_set)
        def label_ratio(labels,label):
            return np.mean(labels == label)
        probablities = []
        for label in label_set:
            probablities.append(label_ratio(labels,label))
        res = 0
        for i in range(num_classes):
            p = probablities[i]
            res -= p * np.log2(p)
        return res
    @staticmethod
    def EntropyA(dataSet,idx):
        dataSet = np.array(dataSet)
        values = set(list(dataSet[:,idx]))
        e = 0
        for value in values:
            e = e + np.sum(dataSet[:,idx] == value)
        return e / dataSet.shape[0]
    def chooseBestFeatureToSplit(self,dataset):
        dataset = np.array(dataset)
        def splitDataSet(dataSet, axis, value):
            dataSet = np.array(dataSet)

            dataMat = dataSet[:,:-1]
            attr = dataMat[:,axis]

            retDataSet = []
            for val in value:
                retDataSet.append(dataSet[attr == val])
            return retDataSet
        max_s = -1
        max_i = 0
        if self.mode == "Entropy":
            for i in range(dataset.shape[1]-2): # 特征个数
                values = set(list(dataset[:,i]))
                datasets = splitDataSet(dataset,i,values)
                s = self.Entropy(dataset)
                for ds in datasets:
                    s = s - self.Entropy(ds)
                if s > max_s:
                    max_s = s
                    max_i = i
        elif self.mode == "C4.5":
            for i in range(dataset.shape[1]-2): # 特征个数
                values = set(list(dataset[:,i]))

                datasets = splitDataSet(dataset,i,values)

                s = self.Entropy(dataset)
                for ds in datasets:
                    s = s - ds.shape[0]/dataset.shape[0] * self.KL_divergence(ds)
                ha = self.EntropyA(dataset,i)
                s = s/ha
                if s > max_s:
                    max_s = s
                    max_i = i
        else:
            for i in range(dataset.shape[1]-2): # 特征个数
                values = set(list(dataset[:,i]))

                datasets = splitDataSet(dataset,i,values)

                s0 = self.KL_divergence(dataset)
                s1 = 0.
                for ds in datasets:
                    s1 = s1 + ds.shape[0]/dataset.shape[0] * self.KL_divergence(ds)
                if s1 - s0 > max_s:
                    max_s = s1 - s0
                    max_i = i

        return max_i
def get_dataset():
    dataSet = []
    with open("/home/xueaoru/下载/decision_tree_glass/lenses.txt","r") as f:
        for line in f:
            l = line.split()
            if len(l) == 6:
                temp = l[:4]
                temp.append(l[4] + l[5])
                dataSet.append(temp)
            else:
                dataSet.append(l)
    return dataSet
def get_random_dataset(n = 100):
    labels = [["young","pre","presbyopic"],
                ["myope","hyper"],
                ["no","yes"],
                ["reduced","normal"],
                ["nolenses","soft","hard"]
            ]
    #gts =
    dataSet = []
    for i in range(n):
        dataSet.append([random.choice(labels[i]) for i in range(5)])
    return dataSet
if __name__ == "__main__":
    #dataSet = get_random_dataset(50)
    #dataSet = np.loadtxt("/home/xueaoru/下载/dataset.txt",dtype = np.str)

    dataSet = get_dataset()
    #dataSet = np.array(dataSet)
    #print(dataSet)
    #dataSet = np.array(dataSet,dtype = np.str)
    #print(get_dataset())
    #print(dataSet.shape)
    gt_set = list(set(list(np.array(dataSet)[:,-1])))
    attrs = ['s' + str(i) for i in range(4)]
    #attrs = ['age','prescript','astigmatic','tearRate']
    ds = DecistionTree(dataSet,attrs,mode = "KL")
    ds.random_chosen()
    ds.train(list(range(len(attrs))))

    ds2 = DecistionTree(dataSet,attrs,mode = "Entropy")
    ds2.random_chosen()
    ds2.train(list(range(len(attrs))))
    ds3 = DecistionTree(dataSet,attrs,mode = "C4.5")
    ds3.random_chosen()
    ds3.train(list(range(len(attrs))))
    correct = 0
    id3_correct = 0
    c45_correct = 0
    random_correct = 0
    for i in range(len(dataSet)):
        gt = np.array(dataSet)[i,-1]
        sample = np.array(dataSet)[i,:-1]
        sample = np.reshape(sample,(1,-1))
        if gt == ds2.predict(sample,ds.root):
            id3_correct += 1
        if gt == ds3.predict(sample,ds.root):
            c45_correct += 1
        if gt == ds.predict(sample,ds.root):
            correct += 1
        r = random.choice(gt_set)
        if gt == r:
            random_correct += 1
        #print(gt,ds.predict(sample,ds.root))
    print("random_choice: {}, ID3: {} ,C4.5: {}, KL_divergence: {}".format(random_correct*1.0/len(dataSet),
                                                                            id3_correct*1.0/len(dataSet),
                                                                            c45_correct*1.0/len(dataSet),
                                                                            correct*1.0/len(dataSet)))
    #tree = createTree(dataSet,list(range(len(labels))))