历年NOIP题

做了几天远古老题，发现不可做，于是咕掉。。转而从2005开始。。

1997：

P1549 棋盘问题（2）：搜索，优化搜索顺序，对于第一行第一列先搜小的（但是其实这样是错的，仅仅能过原题）

加强版咕。

1998：

P1011 车站：类似斐波那契，推式子即可。

P1012 拼数：sort cmp:a+b>b+a

P1013 进制位：观察性质发现，一定是n-1进制。

原因：若进制 <n-1 会出现重复字母，若进制 >n-1 则不会进位导致出现更大的数。

判断一个数字是什么：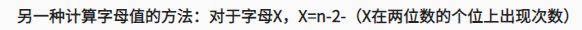

其实就是这样

1999：

P1016 旅行家的预算

P1021 邮票面值设计：直接搜索方案，最后做一个基于值域的背包

2000：

P1004 方格取数：怎么跟传纸条一样啊，，，还是\(f[i][j][k][l]\) 表示一个人是\(i,j\)，另一个人是\(k,l\),

\(f[i][j][k][l]\\=\max(f[i-1][j][k-1][l],f[i-1][j][k][l-1],f[i][j-1][k][l-1],f[i][j-1][k-1][l])\\+a[i][j]+a[k][l]-(i==k\&\&k==l)?a[i][j]:0\)

P1017 进制转换：通常进制转换是先\(%M\)然后\(/M\),但是这道题 \(%M\) 后可能会有负数（负数%负数），所以我们给每个余数强制+（-m）即可。

//远古代码
void turn(int n,int m)
{
    if(n==0) return;
    else
	{
        if(n>0||n%m==0)
		{
			turn(n/m,m);
			printf("%c",c[n%m]);
			return;
		}
        else
		{
			turn(n/m+1,m);
			printf("%c",c[-m+n%m]);
			return;
		}
    }
}

P1018 乘积最大：辣鸡DP+高精（摸）

2005

P1051 谁拿了最多奖学金：模拟。

P1052 过河：我们可以把两个点之间大于 \(t=\operatorname{lcm}(s,s+1,\cdots,t-1,t)\) 的距离缩起来，原因是两点间的距离 \(d \geq t\) 时，一定可以由 \(d\%t\) 跳过来，然后DP。

P1053 篝火晚会：模拟，我们先造出来最后的环。我们发现只要动所有的不满足的位置即可。这样我们可以记下每个点的偏移量，偏移量一样的是一组。

P1054 等价表达式：中缀计算表达式的值，模意义下计算。

const int N=100,M=1000000021,A=20040109;
char s[N];
int n,ans,s1[N],s2[N],t1,t2,d[N<<1];
inline int qpow(int a,int b) { R ret=1;
	for(;b;b>>=1,a=1ll*a*a%M) if(b&1) ret=1ll*ret*a%M; return ret;
}
inline void pop() {
	R a=0,y=s1[t1--],x=s1[t1--];
	switch(s2[t2--]) {
		case '+': a=(x+y)%M; break;
		case '-': a=(x-y+M)%M; break;
		case '*': a=1ll*x*y%M; break;
		case '^': a=qpow(x,y); break;
	} s1[++t1]=a;
}
inline int calc() {
	t1=t2=0;
	for(R i=0,lim=strlen(s);i<lim;++i) {
		if(isdigit(s[i])) { R x=0;
			do x=x*10+(s[i]^48); while(isdigit(s[++i])); --i;
			s1[++t1]=x;
		}
		if(s[i]=='a') s1[++t1]=A;
		if(s[i]=='(') s2[++t2]='(';
		if(s[i]==')') {while(t2&&s2[t2]!='(') pop(); if(t2) --t2;}
		if(d[s[i]]) {while(d[s2[t2]]>=d[s[i]]) pop(); s2[++t2]=s[i];}
	} while(t2) pop(); return s1[t1];
}
inline void main() {
	scanf("%[^\r]",s),getchar();
	d['+']=d['-']=1,d['*']=2,d['^']=3;
	ans=calc();
	n=g();
	for(R i=1;i<=n;++i) {
		scanf("%[^\r]",s),getchar();
		if(calc()==ans) putchar('A'+i-1);
	}
}

2006：

P1063 能量项链：拆环为链+区间DP。

P1064 金明的预算方案：假设我们已经背了前k-1组（数组f），对于第k组，先把主件背到包含前k-1组的背包里（另开一个数组h），然后对所有附件在h数组上跑01背包，然后f=max(f,h),表示不取或取第i组。

P1065 作业调度方案：ri读题读错+数组开小、、、就是个模拟（我还以为是DP）

P1066 2^k进制数：高精+组合数。若\(k|w\)，则方案数\(\sum_{i=2}^{\frac{w}{k}}C(2^k-1,i),i\)代表\(1\)到\(i\)位不为\(0\)；若\(k\nmid w\)，若高位填\(0\)，有\(\sum_{i=2}^{\lfloor\frac{w}{k}\rfloor}C(2^k-1,i)\),否则我们要枚举高位填什么，即\(\sum_{i=1}^{2^{w\%k}-1}C(2^k-1-i,\lfloor\frac{w}{k}\rfloor)\)

2007

P1005 矩阵取数游戏：就是个区间DP，\(f[i][j]=\max(f[i-1][j]+a[i-1]*2^{m-(j-i)-1},f[i][j+1]+a[j+1]*2^{m-(j-i)-1})\),但是又要高精。

P1097 统计数字：sort一遍结束

P1098 字符串的展开：模拟。拿中间(i)的去判两边的(i-1,i+1)。

P1099 树网的核：\(\mathcal{O}(n^3)\)：直接找直径枚举两个端点，然后整个dfs一遍

\(\mathcal{O}(n^2)\)：发现选的部分一定是尽量长，于是确定了左端点，就可以确定右端点，然后dfs

\(\mathcal{O}(nlog(\sum w_i))\)：二分在选择的上的两端点到直径两端点的距离，然后通过dfs，把这段选择区间的点的最长链找出来，判定。

\(\mathcal{O}(n)\)：观察到我们其实可以先求出来直径上每个点不过直径的最长链，然后在直径上跑一个类似滑动窗口的东西。（更优秀的见lyd的书上）。

2008

P1006 传纸条：同方格取数，可以四维，三维，二维DP or 网络流。

P1125 笨小猴：模拟。

P1149 火柴棒等式：预处理出每个数（最大最大也不可能超过1111（8根））要用多少火柴棒，然后枚举 \(A\) 与 \(B\) 。

P1155 双栈排序：刚开始写的贪心。。。然后弃掉了。

我们首先观察到，若有\(i<j<k\ \&\&\ a[k]<a[i]<a[j]\)，那么 \(i,j\) 一定不在一个栈里面。

现在有两个栈，我们可以将不在一个栈中的点连边，然后判一下是否是一个二分图即可确定是否能双栈排序。

排序时注意：能先弹第一个栈的话，一定要先弹掉（字典序更小）。

也可以看看zjp_shadow的题解。

#include<bits/stdc++.h>
#define R register int
using namespace std;
namespace Luitaryi {
inline int g() { R x=0,f=1;
	register char ch; while(!isdigit(ch=getchar())) f=ch=='-'?-1:f;
	do x=x*10+(ch^48); while(isdigit(ch=getchar())); return x*f;
} const int N=1010,Inf=0x7f7f7f7f;
#define pc(x) putchar(x)
int n,a[N],mn[N],co[N];
int stk[2][N],top[2],pos=1;
vector <int> e[N];
inline bool pop(int whi) {
	if(top[whi]&&stk[whi][top[whi]]==pos) {
		pc(whi?'d':'b'),pc(' '),--top[whi],++pos;
		return true;
	}
	return false;
}
inline void push(int x,int whi) {
	if(whi==1) while(pop(0));//先能弹第一个就弹
	while(top[whi]&&stk[whi][top[whi]]<x)
		if(!pop(whi)) pop(whi^1);//弹自己的同时弹另一个
	if(whi==1) while(pop(0));//还是能弹接着弹
	stk[whi][++top[whi]]=x; pc(whi?'c':'a'),pc(' ');
}
inline void main() {
	n=g(); for(R i=1;i<=n;++i) a[i]=g();
	mn[n+1]=n+1;
	for(R i=n;i;--i) mn[i]=min(mn[i+1],a[i]);
	for(R i=1;i<=n;++i) for(R j=i+1;j<=n;++j) if(mn[j+1]<a[i]&&a[i]<a[j])
		e[i].push_back(j),e[j].push_back(i),co[i]=co[j]=-1;
	for(R i=1;i<=n;++i) if(!~co[i]) {
		queue<int> q; q.push(i); co[i]=0;
		while(q.size()) { R u=q.front(); q.pop();
			for(R i=0,lim=e[u].size();i<lim;++i) { R v=e[u][i];
				if(~co[v]&&co[u]!=(co[v]^1)) return (void) puts("0");
				if(!~co[v]) q.push(v);
				co[v]=co[u]^1;
			}
		}
	}
	for(R i=1;i<=n;++i) push(a[i],co[i]);
	register bool flg=true; while(flg) {
		flg=false; while(pop(0)) flg=true; while(pop(1)) flg=true;
	}
}
} signed main() {Luitaryi::main(); return 0;}

2009

P1071 潜伏者：双射，开一个数组模拟即可。

P1072 Hankson 的趣味题：可以直接暴力枚举约数（试除），也可用搜索优化这个过程（枚举每个质因数选了几个）（记住\(10^9\) 以内的约数最多的数约数只有 \(1536\) ）；也有更优秀的做法，见lyd的书。

P1073 最优贸易：跑一边 \((1,u)\) 最长路，跑一边 \((u,n)\) 最短路.

P1074 靶形数独：搜索，当然要按一定顺序搜，我们先把每一行没有出现过的点的数量计算出来，然后排序行，之后对每行的点编号，爆搜即可。。。。

2010

P1540 机器翻译：直接按题意模拟。

P1541 乌龟棋：四维DP，存每种牌的张数。

P1525 关押罪犯：带权 or 种类并查集，把尽量大的边作为矛盾边，只要发现两个点属于同一种颜色 or 同一集合，break；

还可以二分边权然后染色，判断是否是二分图。

P1514 引水入城：记忆化搜索，也可以不记忆化，复杂度也对，我们发现，不同的点覆盖的区间一定是不交的，即不会出现下面的情况：

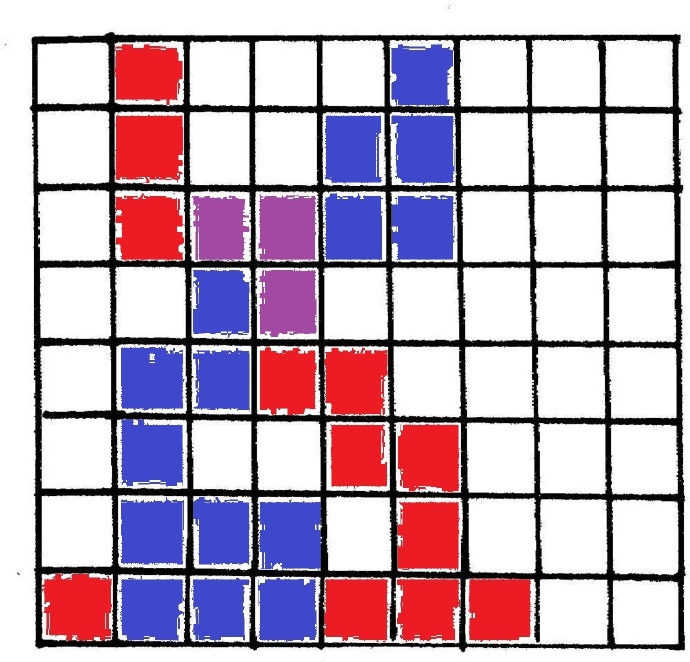
所以我们可以求出第一行每个点覆盖的区间，然后原题就转化为区间覆盖问题。这个问题可以贪心（md怎么又是贪心），详见代码。

bool vis[N][N];
int n,m,cnt,tot,l[N][N],r[N][N],f[N],h[N][N];
struct node { int l,r;
	inline bool operator < (const node& that) const
		{return l<that.l;}
}s[N];
inline void dfs(int x,int y) {
	vis[x][y]=true;
	for(R i=0;i<4;++i) { R xx=x+dx[i],yy=y+dy[i];
		if(xx<1||xx>n||yy<1||yy>m||h[xx][yy]>=h[x][y]) continue;
		if(!vis[xx][yy]) dfs(xx,yy);
		l[x][y]=min(l[xx][yy],l[x][y]);//求出每个点能管辖的最左
		r[x][y]=max(r[xx][yy],r[x][y]);//和最右
	}
}
inline void main() {
	n=g(),m=g(); for(R i=1;i<=n;++i) for(R j=1;j<=m;++j) h[i][j]=g();
	memset(l,0x3f,sizeof l); for(R i=1;i<=m;++i) l[n][i]=r[n][i]=i;
	for(R i=1;i<=m;++i) if(!vis[1][i]) dfs(1,i);
	for(R i=1;i<=m;++i) if(!vis[n][i]) ++cnt;
	if(cnt) return puts("0"),printf("%d\n",cnt),void(); puts("1");
	for(R i=1;i<=m;++i) s[i].l=l[1][i],s[i].r=r[1][i];//,cout<<s[i].l<<' '<<s[i].r<<endl;
	sort(s+1,s+m+1); R p=1,LL=1,RR=0;
	memset(f,0x3f,sizeof f); f[0]=0;
	while(LL<=m) {
		while(s[p].l<=LL&&p<=m) RR=max(RR,s[p].r),++p; //在包含的区间中，尽量往右跳
		++tot,LL=RR+1;
	} printf("%d\n",tot);
}

2011

P1003 铺地毯：模拟，然而正序倒序都行。

P1311 选择客栈：计算以每个点为右端点的方案数，详见代码。

int n,k,P; ll ans;
int c[N],s[101];
inline void main() { n=g(),k=g(),P=g();
	for(R i=1,p,lst=0;i<=n;++i) {
		c[i]=g(),p=g(); if(p<=P) {//把上次小于P的位置到当前位置的点加进桶里
			for(R j=lst+1;j<=i;++j) ++s[c[j]];
			lst=i,ans+=s[c[i]]-1;
		} else ans+=s[c[i]];
	}
	printf("%lld\n",ans);
}

P1312 Mayan游戏：大模拟。。。

一个贪心：只有左边没有块时才考虑左移，否则我们不如右移。

const int N=8;
const int dx[]={-1,1,0,0},dy[]={0,0,-1,1},H=5,L=7;
int n,ansx[N],ansy[N],ansd[N];
int s[N][N][N]; bool vis[N][N];
inline bool ck(int x,int y) {return x<1||x>5||y<1||y>7;}
inline void ins(int d,int x,int y,int dir) {ansx[d]=x,ansy[d]=y,ansd[d]=dir;}
inline void drop(int d) {
	for(R i=0;i<H;++i) { R sz=-1;
		for(R j=0;j<L;++j) if(s[d][i][j])
			s[d][i][++sz]=s[d][i][j];
		while(++sz<L) s[d][i][sz]=0;
	}
}
inline void del(int d) { register bool flg=true;
	while(flg) { drop(d);//让块掉落
		flg=false; for(R i=0;i<H;++i) for(R j=0;j<L;++j) if(s[d][i][j]) {
			if(i<3) if(s[d][i][j]==s[d][i+1][j]&&s[d][i][j]==s[d][i+2][j]) //判横向的3个
				flg=vis[i][j]=vis[i+1][j]=vis[i+2][j]=true;
			if(j<5) if(s[d][i][j]==s[d][i][j+1]&&s[d][i][j]==s[d][i][j+2]) //判纵向的3个
				flg=vis[i][j]=vis[i][j+1]=vis[i][j+2]=true;
		} for(R i=0;i<H;++i) for(R j=0;j<L;++j)
			if(vis[i][j]) s[d][i][j]=vis[i][j]=0;//清除
	}
}
inline bool dfs(int d) {
	memcpy(s[d],s[d-1],sizeof s[d-1]); del(d); if(d==n+1) {
		for(R i=0;i<H;++i) if(s[d][i][0]) return false;//检查当前局面
		return true;
	} for(R i=0;i<H;++i) for(R j=0;j<L;++j) if(s[d][i][j]) {
		if(i<4&&s[d][i][j]!=s[d][i+1][j]) {//向右交换（若相同颜色则不交换的剪枝可能是假的）
			ins(d,i,j,1),swap(s[d][i][j],s[d][i+1][j]);
			if(dfs(d+1)) return true; swap(s[d][i][j],s[d][i+1][j]);
		} if(i&&!s[d][i-1][j]) {//向左移动
			ins(d,i,j,-1),swap(s[d][i][j],s[d][i-1][j]);
			if(dfs(d+1)) return true; swap(s[d][i][j],s[d][i-1][j]);
		}
	} return false;
}
inline void main() {
	n=g(); for(R i=0;i<H;++i) for(R j=0,x=g();x;++j,x=g()) s[0][i][j]=x;
	if(dfs(1)) for(R i=1;i<=n;++i) printf("%d %d %d\n",ansx[i],ansy[i],ansd[i]);
	else puts("-1");
}

P1313 计算系数：二项式定理。

P1314 聪明的质监员：二分 \(W\) 的值。然后每次 \(\mathcal{O}(n)\) 重新计算前缀和，然后 \(\mathcal{O}(m)\) 计算代价。

int n,m,mn=1e9,mx=0,w[N],v[N],l[N],r[N];
ll S,s[N],sum[N],ans=1e17;
inline bool ck(int x) { register ll ret=0;
	memset(s,0,sizeof s),memset(sum,0,sizeof sum);
	for(R i=1;i<=n;++i) if(w[i]>=x) s[i]=s[i-1]+1,sum[i]=sum[i-1]+v[i];
	else s[i]=s[i-1],sum[i]=sum[i-1];
	for(R i=1;i<=m;++i) ret+=(s[r[i]]-s[l[i]-1])*(sum[r[i]]-sum[l[i]-1]);
	ans=min(ans,llabs(ret-S)); return ret>S;
}
inline void main() {
	n=g(),m=g(),S=g(); for(R i=1;i<=n;++i)
		w[i]=g(),v[i]=g(),mn=min(mn,w[i]),mx=max(mx,w[i]);
	for(R i=1;i<=m;++i) l[i]=g(),r[i]=g(); R LL=0,RR=mx+1;
	while(LL<RR) { R md=LL+RR>>1;
		if(ck(md)) LL=md+1; else RR=md;
	} printf("%lld\n",ans);
}

P1315 观光公交：好题，\(\mathcal{O}(kn)\) 的贪心（自己简直zz）

对于每个加速器，我们只用找到他能贡献的最大人数即可，每次重复这个过程。

显然，当一个景点最晚到的人比 从1号点到这个点的时间还要短时，我们就不用考虑后面的点了。

struct node {int a,b,t;}s[M];
int n,m,k,low[N],dst[N],t[N],c[N],ans;
//dst[i]从1到i用时，low[i]到点i最晚的游客
inline void main() {
	n=g(),m=g(),k=g();
	for(R i=1;i<n;++i) t[i]=g();
	for(R i=1;i<=m;++i) {
		s[i].t=g(),s[i].a=g(),s[i].b=g();
		low[s[i].a]=max(low[s[i].a],s[i].t);
		++c[s[i].b];
	} R lst=0;
	for(R i=1;i<=n;++i) dst[i]=lst,lst=max(dst[i],low[i]),lst+=t[i];
	while(k--) {
		R mx=0,tmp=0,pos=0;
		for(R i=2,j;i<=n;i=j+1) { tmp=0;
			while(!t[i-1]) ++i;
			for(j=i;j<=n;++j) {
				tmp+=c[j];
				if(dst[j]<=low[j]) break;
			}
			if(tmp>mx) mx=tmp,pos=i;
		} --t[pos-1];//在路上用加速器
		for(R i=pos;i<=n;++i) {
			--dst[i]; if(dst[i]<low[i]) break;
		}
	} for(R i=1;i<=m;++i) ans+=dst[s[i].b]-s[i].t;
	printf("%d\n",ans);
}

2012

P1079 Vigenère 密码：模拟；

P1080 国王游戏：贪心，邻项交换；

P1081 开车旅行：倍增DP，先排序，然后用链表串起来这样，预处理出最小点和次小点；

const int N=100010,L=16,L2=2;
int n,m,h[N],pos[N],to1[N],to2[N],ans;
ll f[L+1][N][2],d1[L+1][N][2],d2[L+1][N][2],A,B,ansA,ansB;
struct node { int h,id,l,r;
	inline bool operator < (const node& that) const {return h<that.h;}
}a[N];
inline bool ck(int l,int r,int md) {
	if(!l) return 0; if(!r) return 1;
	return a[md].h-a[l].h<=a[r].h-a[md].h;
}
inline void solve(int i,ll d) {
	A=B=0; register bool k=0;
	for(R t=L;~t;--t) if(f[t][i][k]&&A+B+d1[t][i][k]+d2[t][i][k]<=d) {
		A+=d1[t][i][k],B+=d2[t][i][k]; if(i==0) k^=1; i=f[t][i][k];
	}
}
inline void main() {
	n=g(); for(R i=1;i<=n;++i) h[i]=a[i].h=g(),a[i].id=i;
	sort(a+1,a+n+1); for(R i=1;i<=n;++i) pos[a[i].id]=i,a[i].l=i-1,a[i].r=i+1; a[n].r=0;
	for(R i=1;i<=n;++i) { R l=a[pos[i]].l,r=a[pos[i]].r;
		if(ck(l,r,pos[i])) { to2[i]=a[l].id; //cout<<
			if(ck(a[l].l,r,pos[i])) to1[i]=a[a[l].l].id; else to1[i]=a[r].id;
		} else { to2[i]=a[r].id;
			if(ck(l,a[r].r,pos[i])) to1[i]=a[l].id; else to1[i]=a[a[r].r].id;
		} if(l) a[l].r=r; if(r) a[r].l=l;
	}
	for(R i=1;i<=n;++i) {
		if(to1[i]) f[0][i][0]=to1[i],d1[0][i][0]=abs(h[i]-h[to1[i]]);
		if(to2[i]) f[0][i][1]=to2[i],d2[0][i][1]=abs(h[i]-h[to2[i]]);
		d1[0][i][1]=d2[0][i][0]=0;
	} for(R t=1;t<=L;++t) for(R i=1;i<=n;++i) for(R j=0,k;j<L2;++j) {
		if(t==1) k=j^1; else k=j;
		if(f[t-1][i][j])
			f[t][i][j]=f[t-1][f[t-1][i][j]][k],
			d1[t][i][j]=d1[t-1][i][j]+d1[t-1][f[t-1][i][j]][k],
			d2[t][i][j]=d2[t-1][i][j]+d2[t-1][f[t-1][i][j]][k];
	} R x0=g(); ansA=1;
	for(R i=1;i<=n;++i) {
		solve(i,x0); if(!B) A=1;
		if(A*ansB<ansA*B||(A*ansB==ansA*B&&h[i]>h[ans])) ansA=A,ansB=B,ans=i;
	} printf("%d\n",ans); m=g();
	while(m--) {R p=g(),d=g(); solve(p,d); printf("%lld %lld\n",A,B);}
}

P1082 同余方程：exgcd；

P1083 借教室：对于每个操作，我们差分标记，检查时用前缀和，若发现不合法倒着撤销每一次操作，直到合法。

P1084 疫情控制：二分+倍增+贪心。

int n,m,cnt;
struct node {int u; ll res; node() {}
	node(int _u,ll _res) {u=_u,res=_res;}
	inline bool operator < (const node& that) const {return res<that.res;}
}mem[N];
int vr[N<<1],nxt[N<<1],fir[N],w[N<<1],fa[N][B+1],d[N],t[N],mem1[N],mem2[N];
bool flg[N],cal[N];
ll dis[N][B+1],mx;
inline void add(int u,int v,int ww) {
	vr[++cnt]=v,nxt[cnt]=fir[u],fir[u]=cnt,w[cnt]=ww;
	vr[++cnt]=u,nxt[cnt]=fir[v],fir[v]=cnt,w[cnt]=ww;
}
inline void dfs(int u) {
	for(R i=fir[u];i;i=nxt[i]) { R v=vr[i];
		if(d[v]) continue; dis[v][0]=w[i],fa[v][0]=u,d[v]=d[u]+1; dfs(v);
	}
}
inline bool calc(int u,int fa) { register bool son=true;
	if(flg[u]) return false;
	for(R i=fir[u];i;i=nxt[i]) { R v=vr[i];
		if(v==fa) continue; son=false; if(calc(v,u)) return true;
	} return son;
}
inline bool ck(int lim) { R cnt=0,t1=0,t2=0; //cout<<lim<<endl;
	memset(cal,0,sizeof cal),memset(mem,0,sizeof mem),memset(flg,0,sizeof flg);
	memset(mem1,0,sizeof mem1),memset(mem2,0,sizeof mem2);
	for(R i=1;i<=m;++i) { R u=t[i]; register ll len=0;
		for(R t=B;~t;--t) if(fa[u][t]>1&&len+dis[u][t]<=lim)//向上爬
			len+=dis[u][t],u=fa[u][t];
		if(fa[u][0]==1&&len+dis[u][0]<=lim) mem[++cnt]=node(u,lim-len-dis[u][0]);//能爬到根
		else flg[u]=true;//定住
	}
	for(R i=fir[1];i;i=nxt[i]) { R v=vr[i];
		cal[v]=calc(v,1);//子树中有没被覆盖的叶子
	} sort(mem+1,mem+cnt+1);//
	for(R i=1;i<=cnt;++i) {
		if(cal[mem[i].u]&&mem[i].res<dis[mem[i].u][0]) cal[mem[i].u]=0;//跑不到一个来回还是就定住 （注意之前已经减过一个dis[u][0]了）
		else mem1[++t1]=mem[i].res;//剩下的
	}
	for(R i=fir[1];i;i=nxt[i]) { R v=vr[i];
		if(cal[v]) mem2[++t2]=dis[v][0];//未覆盖的
	}
	if(t1<t2) return false;
	sort(mem1+1,mem1+t1+1),sort(mem2+1,mem2+t2+1);//便于下面的双指针扫描
	R p=1,q=1; while(p<=t1&&q<=t2)
		if(mem1[p]>=mem2[q]) ++p,++q; else ++p;
	return q>t2;
}
inline void main() {
	n=g(); for(R i=1,u,v,w;i<n;++i) u=g(),v=g(),w=g(),add(u,v,w),mx+=w;
	d[1]=1;dfs(1); for(R t=1;t<=B;++t) for(R i=1;i<=n;++i)
		fa[i][t]=fa[fa[i][t-1]][t-1],dis[i][t]=dis[i][t-1]+dis[fa[i][t-1]][t-1];
	m=g(); for(R i=1;i<=m;++i) t[i]=g(); R l=0,r=mx; while(l<r) {
		R md=l+r>>1; if(ck(md)) r=md; else l=md+1;
	} if(r==mx) puts("-1");
	else printf("%d\n",l);
}

2013

P1965 转圈游戏：快速幂+%

模模模

P1966 火柴排队：日，排序。

我们发现，直接双关键字排序求出每个数的排名（感觉只按值排序不一定对，不过你要是稳定排序就OK了），然后显然交换B与交换A是一样的，我们只要交换其中一个就可以，这样我们把B中每个数对应的A中的数原来的位置记录下来即可，然后把B按原来的位置sort回去，求逆序对。

int n,ans,c[N];
inline void add(int x) {for(;x<=n;x+=x&-x) ++c[x];}
inline int query(int x) { R ret=0;
	for(;x;x-=x&-x) ret+=c[x]; return ret;
}
struct node { ll v; int p,id;
	inline bool operator < (const node& that) const
		{return p<that.p;}
}a[N],b[N];
inline bool cmp(const node& _this,const node& _that)
	{return _this.v<_that.v||(_this.v==_that.v&&_this.p<_that.p);}
inline void main() {
	n=g(); for(R i=1;i<=n;++i) a[i].v=g(),a[i].p=i;
	for(R i=1;i<=n;++i) b[i].v=g(),b[i].p=i;
	sort(a+1,a+n+1,cmp),sort(b+1,b+n+1,cmp);
	for(R i=1;i<=n;++i) b[i].id=a[i].p;
	sort(b+1,b+n+1); for(R i=n;i;--i)
		ans=(ans+query(b[i].id))%M,add(b[i].id);
	printf("%d\n",ans);
}

P1967 货车运输：最大生成树+倍增lca && 链上最小值。

P1969 积木大赛：贪心（md为什么又是贪心），见代码。

signed main() {
    int n,a,last=0,ans=0;
    cin>>n;
    for(int i=1;i<=n;i++) {
        cin>>a;
        if(a>last)ans+=(a-last);
        last=a;
    }
    cout<<ans<<endl;
}

P1970 花匠：类似DP，\(f\) 表示最后是下降的的最长长度，\(h\) 表示是最后上升的最长长度。

注意一个贪心，我们不会从更靠前的地方继承。大致看起来最后答案是连续的。

inline void main() {
	R n=g(); R f=1,h=1,lst=g();
	for(R i=2,x;i<=n;++i) { x=g();
		if(x>lst) f=max(f,h+1);
		if(x<lst) h=max(h,f+1);
		lst=x;
	} printf("%d\n",max(f,h));
}

P1979 华容道：注意到我们不能每次都bfs。注意到只有空格子和我们要动的块是相邻的 才是有用状态。注意到各状态之间可以连边。于是我们可以每次跑出初始状态到最终状态的最短路。

复杂度 \(\mathcal{O}(m+q*km),m\leq 16n^2\)

好像边的数组开小了。

const int dx[]={1,-1,0,0},dy[]={0,0,1,-1},N=40,Inf=0x3f3f3f3f,L=4;
int n,m,q,num,cnt; bool a[N][N],flg[N][N],vis[N*N*4];
int id[N][N][L],d[N*N*4];
int vr[N*N*4<<1],nxt[N*N*4<<1],fir[N*N*4<<1],w[N*N*4<<1];
struct node {int x,y,w;node() {} node(int _x,int _y,int _w) {x=_x,y=_y,w=_w;}};
inline void add(int u,int v,int ww) {vr[++cnt]=v,nxt[cnt]=fir[u],fir[u]=cnt,w[cnt]=ww;}
inline int dis(int x1,int y1,int x2,int y2,int x3,int y3) {//x1,y1起点，x2,y2终点，x3,y3不能经过的点
	if(x1==x2&&y1==y2) return 0;
	memset(flg,0,sizeof flg);
	queue<node> q; q.push(node(x1,y1,0)),flg[x1][y1]=true;
	while(q.size()) { register node u=q.front(); q.pop();
		if(u.x==x2&&u.y==y2) return u.w;
		for(R i=0;i<4;++i) { R x=u.x+dx[i],y=u.y+dy[i];
			if(x<1||x>n||y<1||y>m) continue;
			if(flg[x][y]||!a[x][y]) continue;
			if(x==x3&&y==y3) continue;
			q.push(node(x,y,u.w+1)); flg[x][y]=true;
		}
	} return Inf;
}
inline int spfa(int x1,int y1,int x2,int y2,int x3,int y3) {//x1,y1空格子，x2,y2起点，x3,y3终点
	queue<int> q; if(x2==x3&&y2==y3) return 0;
	memset(d,0x3f,sizeof d); R ret=Inf;
	for(R k=0;k<L;++k) if(id[x2][y2][k]) {
		d[id[x2][y2][k]]=dis(x1,y1,x2+dx[k],y2+dy[k],x2,y2);
		q.push(id[x2][y2][k]),vis[id[x2][y2][k]]=1;
	} while(q.size()) { R u=q.front(); q.pop(); vis[u]=false;
		for(R i=fir[u];i;i=nxt[i]) { R v=vr[i];
			if(d[v]>d[u]+w[i]) {
				d[v]=d[u]+w[i]; if(!vis[v]) vis[v]=true,q.push(v);
			}
		}
	} for(R k=0;k<L;++k) if(id[x3][y3][k]) ret=min(ret,d[id[x3][y3][k]]);
	return ret==Inf?-1:ret;
}
inline void main() {
	n=g(),m=g(),q=g(); for(R i=1;i<=n;++i) for(R j=1;j<=m;++j) a[i][j]=g();
	for(R i=1;i<=n;++i) for(R j=1;j<=m;++j) for(R k=0;k<L;++k)
		if(a[i][j]&&a[i+dx[k]][j+dy[k]]) id[i][j][k]=++num;
	for(R i=1;i<=n;++i) for(R j=1;j<=m;++j) for(R k=0;k<L;++k)
		if(id[i][j][k]) add(id[i][j][k],id[i+dx[k]][j+dy[k]][k^1],1);//交换空白块和正常块
	for(R i=1;i<=n;++i) for(R j=1;j<=m;++j) for(R k=0;k<L;++k) for(R l=0;l<L;++l)
		if(k!=l&&id[i][j][k]&&id[i][j][l])
			add(id[i][j][k],id[i][j][l],dis(i+dx[k],j+dy[k],i+dx[l],j+dy[l],i,j));//同块不同白块转移
	for(R i=1;i<=q;++i) {
		R ex=g(),ey=g(),sx=g(),sy=g(),tx=g(),ty=g();
		printf("%d\n",spfa(ex,ey,sx,sy,tx,ty));
	}
}

2014

P1328 生活大爆炸版石头剪刀布：直接模拟。

P1351 联合权值：\(ans=\sum_{u}\sum_{x,(u,x)}\sum_{y,(u,y),y!=x} w_x\times w_y\)

所以每条边只会被枚举两次，所以复杂度\(\mathcal{O}(n)\)

P1941 飞扬的小鸟：完全背包。

P2038 无线网络发射器选址：枚举，模拟。

P2296 寻找道路：bfs 反图一遍，找到终点能到的点集，然后处理出每个点的所有出点是否都是能到终点，然后在合法的点上再bfs一遍。

int n,m,s,t;
bool flg[N];
struct G {
int cnt,vr[M],nxt[M],fir[N],d[N];
queue<int> q;
inline void add(int u,int v)
	{vr[++cnt]=v,nxt[cnt]=fir[u],fir[u]=cnt;}
inline void bfs(int s,int t) {
	q.push(s); d[s]=1; while(q.size()) {
		R u=q.front(); q.pop();
		for(R i=fir[u];i;i=nxt[i]) { R v=vr[i];
			if(flg[v]&&!d[v]) d[v]=d[u]+1,q.push(v);
		}
	}
}
}e1,e2;
inline void main() {
	n=g(),m=g(); for(R i=1,u,v;i<=m;++i)
		u=g(),v=g(),e1.add(u,v),e2.add(v,u);
	s=g(),t=g(); for(R i=1;i<=n;++i) flg[i]=1;
	e2.bfs(t,s); if(!e2.d[s]) return (void) puts("-1");
	for(R u=1;u<=n;++u) { flg[u]=e2.d[u];
		if(flg[u]) for(R i=e1.fir[u];i;i=e1.nxt[i]) {
			R v=e1.vr[i]; if(!e2.d[v]) {flg[u]=false; break;}
		}
	}
	e1.bfs(s,t); if(e1.d[t]) printf("%d\n",e1.d[t]-1);
	else puts("-1");
}

P2312 解方程：模意义下解方程。。。实在不行就双哈希。秦九昭。

2015

P2615 神奇的幻方：模拟。

P2661 信息传递：并查集判环。

P2668 斗地主：

P2540 斗地主增强版：在写正解了。

P2678 跳石头：二分 + 贪心。

P2679 子串：DP，设 \(f[i][j][k][0/1]\) 表示前 \(i\) 位匹配前 \(j\) 位，\(k\) 个子串，\(i\) 是否选了。

P2680 运输计划：先二分将问题转化为判定，现在就是要求是否存在 去掉一条边，使得所有路径的最大值小于二分的答案。

于是可以树上差分。

常数被锤

const int N=300010,L=18;
struct edge {
	int u,v,w,t;
}e[N];
int n,m,cnt,mx;
int vr[N<<1],nxt[N<<1],w[N<<1],W[N],fir[N],d[N],dis[N],f[N][L+1],c[N],s[N];
inline void add(int u,int v,int ww)
	{vr[++cnt]=v,w[cnt]=ww,nxt[cnt]=fir[u],fir[u]=cnt;}
inline void dfs(int u) {
	for(R i=fir[u];i;i=nxt[i]) { R v=vr[i];
		if(d[v]) continue; W[v]=w[i];
		f[v][0]=u; d[v]=d[u]+1; dis[v]=dis[u]+w[i];
		dfs(v);
	}
}
inline int lca(int u,int v) {
	if(d[u]<d[v]) swap(u,v);
	for(R i=L;~i;--i) if(d[f[u][i]]>=d[v]) u=f[u][i];
	if(u==v) return u;
	for(R i=L;~i;--i) if(f[u][i]!=f[v][i]) u=f[u][i],v=f[v][i];
	return f[u][0];
}
inline bool ck(int x) { R tot=0;
	memset(c,0,sizeof(c));
	for(R i=1;i<=m;++i) if(e[i].w>x)
		++tot,++c[e[i].u],++c[e[i].v],c[e[i].t]-=2;
	for(R i=1;i<=n;++i) c[f[s[i]][0]]+=c[s[i]];
	for(R i=n;i;--i) if(tot==c[i]&&mx-W[i]<=x) return true;
	return false;
}
inline bool cmp(const int& a,const int& b) {return d[a]>d[b];}
inline void main() {
	n=g(),m=g();
	for(R i=1,u,v,w;i<n;++i)
		u=g(),v=g(),w=g(),add(u,v,w),add(v,u,w);
	d[1]=1; dfs(1);
	for(R t=1;t<=L;++t) for(R i=1;i<=n;++i) f[i][t]=f[f[i][t-1]][t-1];
	for(R i=1;i<=n;++i) s[i]=i; sort(s+1,s+n+1,cmp);
	for(R i=1;i<=m;++i) {
		e[i].u=g(),e[i].v=g();
		e[i].w=dis[e[i].u]+dis[e[i].v]-2*dis[lca(e[i].u,e[i].v)];
		e[i].t=lca(e[i].u,e[i].v);
		mx=max(mx,e[i].w);
	} R l=0,r=mx+1;
	while(l<r) {
		R md=l+r>>1;
		if(ck(md)) r=md;
		else l=md+1;
	} printf("%d\n",l);
}

2016

P1563 玩具谜题：模拟。

P1600 天天爱跑步：转化条件，转化为深度相关的一些量，然后全局桶维护。其实类似差分思想。

P1850 换教室：期望DP，\(f[i][j][0/1]\) 表示前 \(i\) 个换了了 \(j\) 次教室的方案数，最后一次换没换，直接转移即可（先预处理出最短路）。

P2822 组合数问题：\(\mathcal{O}(n^2)\) 预处理+前缀和。

P2827 蚯蚓：注意到若 \(x_1>x_2\), \(\lfloor px_1 \rfloor + q = \lfloor px_1+q \rfloor \geq \lfloor px_2+pq \rfloor = \lfloor p(x_2+q) \rfloor\)，所以三种蚯蚓都是内部都是单调递减的，于是三个队列维护即可。

P2831 愤怒的小鸟：状压，把是否杀死了某只猪压起来，先预处理 \(i,j\) 两点构成的抛物线覆盖的点集，然后转移时注意我们强制从没有死的最低位的猪转移，即强制杀死没有死的最低位的猪。注意这样尽管有些状态没有被转移到，但是有句话说得好：

即最终的状态是一定能够转移到。

这个思想还是很重要的。

int T,n,m,f[1<<L],s[L][L],low[1<<L]; double x[L],y[L];
inline void calc(double& A,double& B,double x1,double y1,double x2,double y2) {
	A=(x2*y1-x1*y2)/(x1*x2*(x1-x2)),B=(x2*x2*y1-x1*x1*y2)/(x1*x2*(x2-x1));
}
inline bool ck0(const double& x) {return x<eps&&x>-eps;}
inline void main() {
	for(R i=1,p=1;i<(1<<L);++i) { p=0;
		while((i>>p&1)) ++p; low[i]=p;
	}
	T=g(); while(T--) {
		memset(f,0x3f,sizeof f),memset(s,0,sizeof s),f[0]=0; n=g(),g();
		for(R i=0;i<n;++i) scanf("%lf%lf",&x[i],&y[i]);
		for(R i=0;i<n;++i) for(R j=0;j<n;++j) {
			if(ck0(x[i]-x[j])) continue; register double a,b;
			calc(a,b,x[i],y[i],x[j],y[j]);
			if(a>0) continue;
			for(R k=0;k<n;++k) if(ck0(y[k]-a*x[k]*x[k]-b*x[k])) s[i][j]|=(1<<k);
		}
		for(R i=0,lim=(1<<n),p;i<lim;++i) { p=low[i];
			f[i|(1<<p)]=min(f[i|(1<<p)],f[i]+1);
			for(R k=0;k<n;++k) f[i|s[p][k]]=min(f[i|s[p][k]],f[i]+1);
		} printf("%d\n",f[(1<<n)-1]);
	}
}

2017

P3951 小凯的疑惑：其实真的也想exgcd，我们靠推 \(k\) 合法且 \(k-1\) 不合法来得到结论，但是还是这种好像比较好理解：

P3952 时间复杂度：没有大样例调不出来系列、

P3958 奶酪：并查集，能相连的点连边。

P3959 宝藏：咕。

P3953 逛公园：还是记搜吧。。。\(f[u][k]\) 表示 到点 \(u\) ，还可以多跑的长度为 \(k\) 。

拓扑的好题解

int T,n,m,kk,p,d[N],f[N][K]; bool vis[N][K],flg[N];
struct edge { int v,w; edge() {}
	edge(int _v,int _w) {v=_v,w=_w;}
}; vector<edge> e1[N],e2[N];
inline void spfa() {
	memset(d,0x3f,sizeof d),d[1]=0; queue<int> q; q.push(1),flg[1]=1;
	while(q.size()) { R u=q.front(); q.pop(); flg[u]=false;
		for(R i=0,lim=e1[u].size();i<lim;++i) { R v=e1[u][i].v,w=e1[u][i].w;
			if(d[v]>d[u]+w) {
				d[v]=d[u]+w; if(!flg[v]) q.push(v),flg[v]=true;
			}
		}
	}
}
inline int dp(int u,int s) { R ret=0;
	if(s<0||s>kk) return 0; if(vis[u][s]) return vis[u][s]=false,-1;
	if(~f[u][s]) return f[u][s]; vis[u][s]=true;
	for(R i=0,lim=e2[u].size();i<lim;++i) {
		R v=e2[u][i].v,w=e2[u][i].w; R cnt=dp(v,d[u]-d[v]+s-w);
		if(cnt==-1) return vis[u][s]=0,-1;
		ret=(ret+cnt)%p;
	} vis[u][s]=0; if(u==1&&s==0) ++ret;
	f[u][s]=ret; return ret;
}
inline void main() { T=g();
	while(T--) {
		for(R i=1;i<=n;++i) e1[i].clear(),e2[i].clear();
		n=g(),m=g(),kk=g(),p=g(); memset(f,-1,sizeof f);
		for(R i=1,u,v,w;i<=m;++i) u=g(),v=g(),w=g(),
			e1[u].push_back(edge(v,w)),e2[v].push_back(edge(u,w));
		spfa(); R ans=0; for(R i=0,x;i<=kk;++i) { x=dp(n,i);
			if(x==-1) {puts("-1"); goto end;} ans=(ans+x)%p;
		} printf("%d\n",ans); end:;
	}
}

P3960 列队 ：动态开点权值线段树，就是暴力维护一行的顺序，找答案时在权值线段树上根据 \(sz\) 二分。

注意重要部分是get() 函数，作用是得到一个点的初始 \(sz\)

const int N=10000010,M=300010;
ll m; int n,q,tot,L;
int t,ls[N],rs[N],sz[N],siz[M],rt[M]; ll vl[N],ans;
inline int get(int l,int r) {
	if(t==n+1) {
		if(r<=n) return r-l+1;
		if(l<=n) return n-l+1;
		return 0;
	} if(r<=m-1) return r-l+1;
	if(l<=m-1) return m-l; return 0;
}
inline ll query(int& tr,int l,int r,int p) {
	if(!tr) {
		tr=++tot,sz[tr]=get(l,r);
		if(l==r) (vl[tr]=(t==n+1)?l*m:(t-1)*m+l);
	} --sz[tr];
	if(l==r) return vl[tr];
	R md=l+r>>1;
	if((!ls[tr]&&get(l,md)>=p)||sz[ls[tr]]>=p)
		return query(ls[tr],l,md,p);
	else {
		if(!ls[tr]) p-=get(l,md); else p-=sz[ls[tr]];
		return query(rs[tr],md+1,r,p);
	}
}
inline void change(int& tr,int l,int r,int p,ll v) {
	if(!tr) { tr=++tot;
		sz[tr]=get(l,r); if(l==r) vl[tr]=v;
	} ++sz[tr]; if(l==r) return ; R md=l+r>>1;
	if(p<=md) change(ls[tr],l,md,p,v);
	if(p>md) change(rs[tr],md+1,r,p,v);
}
inline void main() {
	n=g(),m=g(),q=g(); L=max((ll)n,m)+q;
	while(q--) { R x=g(),y=g();
		if(y==m) t=n+1,ans=query(rt[t],1,L,x);
		else t=x,ans=query(rt[t],1,L,y);
		printf("%lld\n",ans);
		t=n+1; change(rt[t],1,L,n+(++siz[t]),ans);
		if(y!=m) {
			t=n+1,ans=query(rt[t],1,L,x);
			t=x,change(rt[t],1,L,m-1+(++siz[t]),ans);
		}
	}
}

2018

P5019 铺设道路：贪。。。。。心。

嘀！您的智商余额不足

signed main() {
    int n,a,last=0,ans=0;
    cin>>n;
    for(int i=1;i<=n;i++) {
        cin>>a;
        if(a>last)ans+=(a-last);//不能一块填的
        last=a;
    }
    cout<<ans<<endl;
}

P5020 货币系统 ：先把所有的钱从小到大 sort 一遍，然后背包，若能被比他小的钱表示出来，就没有用。

P5021 赛道修建：二分+贪心。

先二分一个长度 \(x\)，看最后能否拼出 \(m\) 个长度为 \(x\) 的链，具体的，我们在每个点作为链的一端 or 作为链的两个端点的lca时，这条链才会被计算。我们每个点会向上传递一个链的长度（可以为0），然后在点 \(u\) 时我们要计算所有孩子的贡献，我们把所有过点 \(u\) 的链按长度 \(sort\) ,贪心的匹配，得到最大匹配链数；然后再贪波心，我们在能够得到最大链数时，尽量选最大的向上传递。

详见代码：

const int N=50010;
int n,m,crt,cnt,tot,X,sum;
int vr[N<<1],nxt[N<<1],fir[N],w[N<<1],f[N];
vector <int> s[N];
inline void add(int u,int v,int ww) {
	vr[++cnt]=v,nxt[cnt]=fir[u],fir[u]=cnt,w[cnt]=ww;
	vr[++cnt]=u,nxt[cnt]=fir[v],fir[v]=cnt,w[cnt]=ww;
}
inline int ck(int u,int md,int sz) {//二分向上传递的链长。
	R l=0,r=sz-1,ret=0;
	for(;r;--r) { if(r==md) --r;
		while(l<r&&s[u][l]+s[u][r]<X) ++l;
		if(l==md) ++l; if(l>=r) break; ++ret,++l;
	} return ret;
}
inline void dfs(int u,int fa) {
	f[u]=0; s[u].clear();
	for(R i=fir[u];i;i=nxt[i]) { R v=vr[i];
		if(v==fa) continue; dfs(v,u);
		f[v]+=w[i]; if(f[v]>=X) ++tot;//不需要匹配
		else s[u].push_back(f[v]);
	} R sz=s[u].size();
	sort(s[u].begin(),s[u].end()); R crt=0;
	for(R l=0,r=sz-1;r;--r) {
		while(l<r&&s[u][l]+s[u][r]<X) ++l;
		if(l>=r) break; ++crt,++l;
	} tot+=crt;
	if(crt*2==sz) return ;
	R l=0,r=sz-1;
	while(l<r) {
		R md=l+r+1>>1;
		if(ck(u,md,sz)==crt) l=md;
		else r=md-1;
	} f[u]=s[u][l];//向上传递的链
}
inline void main() {
	n=g(),m=g();
	for(R i=1,u,v,w;i<n;++i) u=g(),v=g(),w=g(),add(u,v,w),sum+=w;
	R l=0,r=sum/m;
	while(l<r) {
    R md=l+r+1>>1;
    tot=0,//总链数
    X=md,//二分的长度
    dfs(1,0);
    if(tot>=m) l=md;
    else r=md-1;
	} printf("%d\n",l);
}

P5022 旅行：树直接dfs，基环树暴力断边+卡常。

static char B[1<<15],*S=B,*D=B;
//#define getchar() (S==D&&(D=(S=B)+fread(B,1,1<<15,stdin),S==D)?EOF:*S++)
using namespace std;
inline int g() {
	R ret=0,fix=1; register char ch; while(!isdigit(ch=getchar())) fix=ch=='-'?-1:fix;
	do ret=ret*10+(ch^48); while(isdigit(ch=getchar())); return ret*fix;
} int n,m,tot;
int ans[5010]; bool vis[5010],used[5010][5010];
vector <int> w[5001];
inline void dfs1(int u) { vis[u]=true; ans[++tot]=u;
	for(R i=0,lim=w[u].size();i<lim;++i) { R v=w[u][i];
		if(!vis[v]) dfs1(v);
	}
} int s[5010]; int U,V;
pair<int,int> e[5010];
//inline void find(int u,int fa) { if(flg) return ;
//	stk[++top]
//}
inline void dfs2(int u) { vis[u]=true; s[++tot]=u;
	for(R i=0,lim=w[u].size();i<lim;++i) { R v=w[u][i];
		if((u==U&&v==V)||(u==V&&v==U)) continue;
		if(!vis[v]) dfs2(v);
	}
}
inline bool ck() {for(R i=1;i<=n;++i) if(s[i]!=ans[i]) return ans[i]>s[i];  return false;}
signed main() {
	n=g(),m=g(); for(R i=1,u,v;i<=m;++i) u=g(),v=g(),w[u].push_back(v),w[v].push_back(u),e[i]=make_pair(u,v);
	for(R i=1;i<=n;++i) sort(w[i].begin(),w[i].end());
	if(m==n-1) {
		dfs1(1); for(R i=1;i<=n;++i) printf("%d ",ans[i]);
	} else {
		//for(R u=1;u<=n;++u) for(R j=1;j<=w[u][0];++j) { R v=w[u][j]; add(u,v);}
		for(R i=1;i<=n;++i) ans[i]=n-i+1;
		for(R i=1;i<=m;++i) {
			tot=0; memset(vis,0,sizeof(vis)); U=e[i].first,V=e[i].second;
			dfs2(1); if(tot==n&&ck()) memcpy(ans,s,sizeof(s));
		} for(R i=1;i<=n;++i) printf("%d ",ans[i]);
	}
}

P5049 旅行（数据加强版）：贪心，考虑只有遍历到环上，且存在一个没有遍历的祖先小于当前的点中的最小值

const int N=500010,Inf=0x3f3f3f3f;
vector<int> e[N];
int n,m,stk[N],top;
bool vis[N],in[N],ins[N],flg;
inline void dfs1(int u,int fa) {
	vis[u]=ins[u]=true,stk[++top]=u;
	for(R v:e[u]) {
		if(v==fa||in[v]) continue;
		if(vis[v]&&ins[v])
			do in[stk[top]]=true,ins[stk[top]]=false; while(stk[top--]!=v);
		else dfs1(v,u);
	} vis[u]=false; if(!in[u]) --top;//找环
}
inline void dfs(int u,int mn) {
	if(vis[u]) return ;
	vis[u]=true,printf("%d ",u); R t=Inf,fir=0;
	if(in[u]&&!flg) { R p=0;
		for(;p<e[u].size();++p) {
			if(vis[e[u][p]]) continue; //访问过
			if(in[e[u][p]]) break; //在环上
      //（这一部分不算在最小点中，因为这一部分直接访问再回溯即可）
		} ++p; //跳过当前节点(在环上)
		for(;p<e[u].size();++p) {
			if(vis[e[u][p]]) continue;
			t=min(e[u][p],t);
		}
	} if(t==Inf) t=mn;//继承上一个
	for(R v:e[u]) {
		if(vis[v]) continue;
		if(in[u]&&in[v]&&!flg) if(v>t) {flg=1; continue;}//用掉一次
		dfs(v,t);
	}
}
inline void main() {
	n=g(),m=g(); for(R i=1,u,v;i<=m;++i) u=g(),v=g(),e[u].push_back(v),e[v].push_back(u);
	for(R i=1;i<=n;++i) sort(e[i].begin(),e[i].end());
	if(n==m) dfs1(1,0);
	memset(vis,0,sizeof vis); dfs(1,Inf);
}

P5023 填数游戏：咕。

P5024 保卫王国：倍增DP，预处理子树内的代价 \(f[u][0/1]\) ，子树外代价 \(d[u][0/1]\)，和倍增的链 \([u,u的 2^k 次方祖先]\) 两个端点及对应的代价 \(h[u][k][0/1][0/1]\)

const int N=100010,L=16,SZ=16; const ll Inf=0x3f3f3f3f3f3f3f3fll;
int n,m,cnt; set<pair<int,int> >s;
int vr[N<<1],nxt[N<<1],fir[N],dep[N],c[N],fa[N][L+1];
ll d[N][2],f[N][2],h[N][L+1][2][2];
inline void add(int u,int v) {
	vr[++cnt]=v,nxt[cnt]=fir[u],fir[u]=cnt;
	vr[++cnt]=u,nxt[cnt]=fir[v],fir[v]=cnt;
}
inline void pre1(int u) { f[u][1]=c[u];
	for(R i=fir[u];i;i=nxt[i]) { R v=vr[i];
		if(dep[v]) continue; dep[v]=dep[u]+1,fa[v][0]=u; pre1(v);
		f[u][0]+=f[v][1],f[u][1]+=min(f[v][0],f[v][1]);//计算子树内的贡献
	}
}
inline void pre2(int u) {
	for(R i=fir[u];i;i=nxt[i]) { R v=vr[i];
		if(v==fa[u][0]) continue;
		d[v][0]=d[u][1]+f[u][1]-min(f[v][0],f[v][1]); //父亲子树外+父亲子树内-自己子树内
		d[v][1]=min(d[u][0]+f[u][0]-f[v][1],d[v][0]); //若父亲是0，则自己必须是1；
		//或者父亲是1，则按上面的计算;
		//之所以可以这样，依赖于子树内的贡献的计算（就是上面如何计算的，就反着来）；
		pre2(v);
	}
}
inline ll solve(int u,int x,int v,int y) {
	if(dep[u]<dep[v]) swap(u,v),swap(x,y);
	register ll tu[2],tv[2],mu[2],mv[2];
	memset(mu,0x3f,SZ),memset(mv,0x3f,SZ);
	mu[x]=f[u][x],mv[y]=f[v][y];
	for(R t=L;~t;--t) if(dep[fa[u][t]]>=dep[v]) {
		memset(tu,0x3f,SZ);
		for(R i=0;i<=1;++i) for(R j=0;j<=1;++j)
			tu[i]=min(tu[i],mu[j]+h[u][t][j][i]);//注意要枚举转移方式。
		memcpy(mu,tu,SZ); u=fa[u][t];
	}
	if(u==v) return mu[y]+d[u][y];
	for(R t=L;~t;--t) if(fa[u][t]!=fa[v][t]) {
		memset(tu,0x3f,SZ),memset(tv,0x3f,SZ);
		for(R i=0;i<=1;++i) for(R j=0;j<=1;++j)
			tu[i]=min(tu[i],mu[j]+h[u][t][j][i]),
			tv[i]=min(tv[i],mv[j]+h[v][t][j][i]);
		memcpy(mu,tu,SZ),memcpy(mv,tv,SZ);
		u=fa[u][t],v=fa[v][t];
	} R lca=fa[u][0];
	register ll ans0=f[lca][0]-f[u][1]-f[v][1]+mu[1]+mv[1]+d[lca][0];//枚举LCA状态
	register ll ans1=f[lca][1]-min(f[u][0],f[u][1])-min(f[v][0],f[v][1])
    											+min(mu[0],mu[1])+min(mv[0],mv[1])+d[lca][1];
	return min(ans0,ans1);
}
inline void main() {
	n=g(),m=g(); g(); for(R i=1;i<=n;++i) c[i]=g();
	for(R i=1,u,v;i<n;++i) u=g(),v=g(),add(u,v),
		s.insert(make_pair(u,v)),s.insert(make_pair(v,u));
	dep[1]=1,pre1(1),pre2(1);
	for(R u=1;u<=n;++u)
		h[u][0][0][0]=Inf,h[u][0][1][0]=f[fa[u][0]][0]-f[u][1],//注意初始化
		h[u][0][0][1]=f[fa[u][0]][1]-min(f[u][0],f[u][1]),
		h[u][0][1][1]=f[fa[u][0]][1]-min(f[u][0],f[u][1]);
	for(R t=1;t<=L;++t) {
		for(R u=1;u<=n;++u) { R tmp=fa[u][t-1]; fa[u][t]=fa[tmp][t-1];
			for(R i=0;i<=1;++i) for(R j=0;j<=1;++j) { h[u][t][i][j]=Inf;
				for(R k=0;k<=1;++k)
					h[u][t][i][j]=min(h[u][t][i][j],h[u][t-1][i][k]+h[tmp][t-1][k][j]);
			}
		}
	}
	while(m--) {
		R u=g(),x=g(),v=g(),y=g();
		if(!x&&!y&&s.count(make_pair(u,v))) {puts("-1"); continue;}
		printf("%lld\n",solve(u,x,v,y));
	}
}