WGS84坐标和UTM坐标的转换

如题。做了一个Demo,主要是把最后面的参考资料1里面的脚本改成了C语言版本的.

代码:

 #ifndef __COORCONV_H__
 #define __COORCONV_H__

 #include <cmath>

 double pi = 3.14159265358979;

 /* Ellipsoid model constants (actual values here are for WGS84) */
 double sm_a = 6378137.0;
 double sm_b = 6356752.314;
 double sm_EccSquared = 6.69437999013e-03;
 double UTMScaleFactor = 0.9996;

 typedef struct tagUTMCorr
 {
     double x;
     double y;
 }UTMCoor;

 typedef struct tagWGS84Corr
 {
     double lat;
     double log;
 }WGS84Corr;
 /*
 * DegToRad
 *
 * Converts degrees to radians.
 *
 */
 inline double DegToRad (double deg)
 {
     return (deg / 180.0 * pi);
 }

 /*
 * RadToDeg
 *
 * Converts radians to degrees.
 *
 */
 inline double RadToDeg (double rad)
 {
     return (rad / pi * 180.0);
 }

 /*
 * ArcLengthOfMeridian
 *
 * Computes the ellipsoidal distance from the equator to a point at a
 * given latitude.
 *
 * Reference: Hoffmann-Wellenhof, B., Lichtenegger, H., and Collins, J.,
 * GPS: Theory and Practice, 3rd ed.  New York: Springer-Verlag Wien, 1994.
 *
 * Inputs:
 *     phi - Latitude of the point, in radians.
 *
 * Globals:
 *     sm_a - Ellipsoid model major axis.
 *     sm_b - Ellipsoid model minor axis.
 *
 * Returns:
 *     The ellipsoidal distance of the point from the equator, in meters.
 *
 */
 double ArcLengthOfMeridian (double phi)
 {
     double alpha, beta, gamma, delta, epsilon, n;
     double result;

     /* Precalculate n */
     n = (sm_a - sm_b) / (sm_a + sm_b);

     /* Precalculate alpha */
     alpha = ((sm_a + sm_b) / 2.0) * (1.0 + (pow(n, 2.0) / 4.0) + (pow(n, 4.0) / 64.0));

     /* Precalculate beta */
     beta = (-3.0 * n / 2.0) + (9.0 * pow(n, 3.0) / 16.0) + (-3.0 * pow(n, 5.0) / 32.0);

     /* Precalculate gamma */
     gamma = (15.0 * pow(n, 2.0) / 16.0) + (-15.0 * pow(n, 4.0) / 32.0);

     /* Precalculate delta */
     delta = (-35.0 * pow(n, 3.0) / 48.0) + (105.0 * pow(n, 5.0) / 256.0);

     /* Precalculate epsilon */
     epsilon = (315.0 * pow(n, 4.0) / 512.0);

     /* Now calculate the sum of the series and return */
     result = alpha * (phi + (beta * sin(2.0 * phi)) + (gamma * sin(4.0 * phi)) + (delta * sin(6.0 * phi)) + (epsilon * sin(8.0 * phi)));

     return result;
 }

 /*
 * UTMCentralMeridian
 *
 * Determines the central meridian for the given UTM zone.
 *
 * Inputs:
 *     zone - An integer value designating the UTM zone, range [1,60].
 *
 * Returns:
 *   The central meridian for the given UTM zone, in radians, or zero
 *   if the UTM zone parameter is outside the range [1,60].
 *   Range of the central meridian is the radian equivalent of [-177,+177].
 *
 */
 inline double UTMCentralMeridian (int zone)
 {
     return DegToRad(-183.0 + (zone * 6.0));
 }

 /*
 * FootpointLatitude
 *
 * Computes the footpoint latitude for use in converting transverse
 * Mercator coordinates to ellipsoidal coordinates.
 *
 * Reference: Hoffmann-Wellenhof, B., Lichtenegger, H., and Collins, J.,
 *   GPS: Theory and Practice, 3rd ed.  New York: Springer-Verlag Wien, 1994.
 *
 * Inputs:
 *   y - The UTM northing coordinate, in meters.
 *
 * Returns:
 *   The footpoint latitude, in radians.
 *
 */
 double FootpointLatitude (double y)
 {
     double y_, alpha_, beta_, gamma_, delta_, epsilon_, n;
     double result;

     /* Precalculate n (Eq. 10.18) */
     n = (sm_a - sm_b) / (sm_a + sm_b);

     /* Precalculate alpha_ (Eq. 10.22) */
     /* (Same as alpha in Eq. 10.17) */
     alpha_ = ((sm_a + sm_b) / 2.0) * ( + (pow(n, 2.0) / ) + (pow(n, 4.0) / ));

     /* Precalculate y_ (Eq. 10.23) */
     y_ = y / alpha_;

     /* Precalculate beta_ (Eq. 10.22) */
     beta_ = (3.0 * n / 2.0) + (-27.0 * pow(n, 3.0) / 32.0) + (269.0 * pow(n, 5.0) / 512.0);

     /* Precalculate gamma_ (Eq. 10.22) */
     gamma_ = (21.0 * pow(n, 2.0) / 16.0) + (-55.0 * pow(n, 4.0) / 32.0);

     /* Precalculate delta_ (Eq. 10.22) */
     delta_ = (151.0 * pow (n, 3.0) / 96.0)    + (-417.0 * pow (n, 5.0) / 128.0);

     /* Precalculate epsilon_ (Eq. 10.22) */
     epsilon_ = (1097.0 * pow(n, 4.0) / 512.0);

     /* Now calculate the sum of the series (Eq. 10.21) */
     result = y_ + (beta_ * sin(2.0 * y_)) + (gamma_ * sin(4.0 * y_)) + (delta_ * sin(6.0 * y_)) + (epsilon_ * sin(8.0 * y_));

     return result;
 }

 /*
 * MapLatLonToXY
 *
 * Converts a latitude/longitude pair to x and y coordinates in the
 * Transverse Mercator projection.  Note that Transverse Mercator is not
 * the same as UTM; a scale factor is required to convert between them.
 *
 * Reference: Hoffmann-Wellenhof, B., Lichtenegger, H., and Collins, J.,
 * GPS: Theory and Practice, 3rd ed.  New York: Springer-Verlag Wien, 1994.
 *
 * Inputs:
 *    phi - Latitude of the point, in radians.
 *    lambda - Longitude of the point, in radians.
 *    lambda0 - Longitude of the central meridian to be used, in radians.
 *
 * Outputs:
 *    xy - A 2-element array containing the x and y coordinates
 *         of the computed point.
 *
 * Returns:
 *    The function does not return a value.
 *
 */
 void MapLatLonToXY (double phi, double lambda, double lambda0, UTMCoor &xy)
 {
     double N, nu2, ep2, t, t2, l;
     double l3coef, l4coef, l5coef, l6coef, l7coef, l8coef;
     double tmp;

     /* Precalculate ep2 */
     ep2 = (pow(sm_a, 2.0) - pow(sm_b, 2.0)) / pow(sm_b, 2.0);

     /* Precalculate nu2 */
     nu2 = ep2 * pow(cos(phi), 2.0);

     /* Precalculate N */
     N = pow(sm_a, 2.0) / (sm_b * sqrt( + nu2));

     /* Precalculate t */
     t = tan (phi);
     t2 = t * t;
     tmp = (t2 * t2 * t2) - pow (t, 6.0);

     /* Precalculate l */
     l = lambda - lambda0;

     /* Precalculate coefficients for l**n in the equations below
     so a normal human being can read the expressions for easting
     and northing
     -- l**1 and l**2 have coefficients of 1.0 */
     l3coef = 1.0 - t2 + nu2;

     l4coef = 5.0 - t2 +  * nu2 + 4.0 * (nu2 * nu2);

     l5coef = 5.0 - 18.0 * t2 + (t2 * t2) + 14.0 * nu2 - 58.0 * t2 * nu2;

     l6coef = 61.0 - 58.0 * t2 + (t2 * t2) + 270.0 * nu2    - 330.0 * t2 * nu2;

     l7coef = 61.0 - 479.0 * t2 + 179.0 * (t2 * t2) - (t2 * t2 * t2);

     l8coef = 1385.0 - 3111.0 * t2 + 543.0 * (t2 * t2) - (t2 * t2 * t2);

     /* Calculate easting (x) */
     xy.x = N * cos (phi) * l + (N / 6.0 * pow(cos(phi), 3.0) * l3coef * pow(l, 3.0))
         + (N / 120.0 * pow(cos(phi), 5.0) * l5coef * pow(l, 5.0))
         + (N / 5040.0 * pow(cos (phi), 7.0) * l7coef * pow(l, 7.0));

     /* Calculate northing (y) */
     xy.y = ArcLengthOfMeridian (phi)
         + (t / 2.0 * N * pow(cos(phi), 2.0) * pow(l, 2.0))
         + (t / 24.0 * N * pow(cos(phi), 4.0) * l4coef * pow(l, 4.0))
         + (t / 720.0 * N * pow(cos(phi), 6.0) * l6coef * pow(l, 6.0))
         + (t / 40320.0 * N * pow(cos(phi), 8.0) * l8coef * pow(l, 8.0));
 }

 /*
 * MapXYToLatLon
 *
 * Converts x and y coordinates in the Transverse Mercator projection to
 * a latitude/longitude pair.  Note that Transverse Mercator is not
 * the same as UTM; a scale factor is required to convert between them.
 *
 * Reference: Hoffmann-Wellenhof, B., Lichtenegger, H., and Collins, J.,
 *   GPS: Theory and Practice, 3rd ed.  New York: Springer-Verlag Wien, 1994.
 *
 * Inputs:
 *   x - The easting of the point, in meters.
 *   y - The northing of the point, in meters.
 *   lambda0 - Longitude of the central meridian to be used, in radians.
 *
 * Outputs:
 *   philambda - A 2-element containing the latitude and longitude
 *               in radians.
 *
 * Returns:
 *   The function does not return a value.
 *
 * Remarks:
 *   The local variables Nf, nuf2, tf, and tf2 serve the same purpose as
 *   N, nu2, t, and t2 in MapLatLonToXY, but they are computed with respect
 *   to the footpoint latitude phif.
 *
 *   x1frac, x2frac, x2poly, x3poly, etc. are to enhance readability and
 *   to optimize computations.
 *
 */
 void MapXYToLatLon (double x, double y, double lambda0, WGS84Corr &philambda)
 {
     double phif, Nf, Nfpow, nuf2, ep2, tf, tf2, tf4, cf;
     double x1frac, x2frac, x3frac, x4frac, x5frac, x6frac, x7frac, x8frac;
     double x2poly, x3poly, x4poly, x5poly, x6poly, x7poly, x8poly;

     /* Get the value of phif, the footpoint latitude. */
     phif = FootpointLatitude (y);

     /* Precalculate ep2 */
     ep2 = (pow(sm_a, 2.0) - pow(sm_b, 2.0))    / pow(sm_b, 2.0);

     /* Precalculate cos (phif) */
     cf = cos (phif);

     /* Precalculate nuf2 */
     nuf2 = ep2 * pow (cf, 2.0);

     /* Precalculate Nf and initialize Nfpow */
     Nf = pow(sm_a, 2.0) / (sm_b * sqrt( + nuf2));
     Nfpow = Nf;

     /* Precalculate tf */
     tf = tan (phif);
     tf2 = tf * tf;
     tf4 = tf2 * tf2;

     /* Precalculate fractional coefficients for x**n in the equations
     below to simplify the expressions for latitude and longitude. */
     x1frac = 1.0 / (Nfpow * cf);

     Nfpow *= Nf;   /* now equals Nf**2) */
     x2frac = tf / (2.0 * Nfpow);

     Nfpow *= Nf;   /* now equals Nf**3) */
     x3frac = 1.0 / (6.0 * Nfpow * cf);

     Nfpow *= Nf;   /* now equals Nf**4) */
     x4frac = tf / (24.0 * Nfpow);

     Nfpow *= Nf;   /* now equals Nf**5) */
     x5frac = 1.0 / (120.0 * Nfpow * cf);

     Nfpow *= Nf;   /* now equals Nf**6) */
     x6frac = tf / (720.0 * Nfpow);

     Nfpow *= Nf;   /* now equals Nf**7) */
     x7frac = 1.0 / (5040.0 * Nfpow * cf);

     Nfpow *= Nf;   /* now equals Nf**8) */
     x8frac = tf / (40320.0 * Nfpow);

     /* Precalculate polynomial coefficients for x**n.
     -- x**1 does not have a polynomial coefficient. */
     x2poly = -1.0 - nuf2;

     x3poly = -1.0 -  * tf2 - nuf2;

     x4poly = 5.0 + 3.0 * tf2 + 6.0 * nuf2 - 6.0 * tf2 * nuf2 - 3.0 * (nuf2 *nuf2) - 9.0 * tf2 * (nuf2 * nuf2);

     x5poly = 5.0 + 28.0 * tf2 + 24.0 * tf4 + 6.0 * nuf2 + 8.0 * tf2 * nuf2;

     x6poly = -61.0 - 90.0 * tf2 - 45.0 * tf4 - 107.0 * nuf2    + 162.0 * tf2 * nuf2;

     x7poly = -61.0 - 662.0 * tf2 - 1320.0 * tf4 - 720.0 * (tf4 * tf2);

     x8poly = 1385.0 + 3633.0 * tf2 + 4095.0 * tf4 +  * (tf4 * tf2);

     /* Calculate latitude */
     philambda.lat = phif + x2frac * x2poly * (x * x) + x4frac * x4poly * pow(x, 4.0) + x6frac * x6poly * pow(x, 6.0) + x8frac * x8poly * pow(x, 8.0);

     /* Calculate longitude */
     philambda.log = lambda0 + x1frac * x + x3frac * x3poly * pow(x, 3.0) + x5frac * x5poly * pow(x, 5.0) + x7frac * x7poly * pow(x, 7.0);
 }

 /*
 * LatLonToUTMXY
 *
 * Converts a latitude/longitude pair to x and y coordinates in the
 * Universal Transverse Mercator projection.
 *
 * Inputs:
 *   lat - Latitude of the point, in radians.
 *   lon - Longitude of the point, in radians.
 *   zone - UTM zone to be used for calculating values for x and y.
 *          If zone is less than 1 or greater than 60, the routine
 *          will determine the appropriate zone from the value of lon.
 *
 * Outputs:
 *   xy - A 2-element array where the UTM x and y values will be stored.
 *
 * Returns:
 *   void
 *
 */
 void LatLonToUTMXY (double lat, double lon, int zone, UTMCoor &xy)
 {
     MapLatLonToXY (lat, lon, UTMCentralMeridian(zone), xy);

     /* Adjust easting and northing for UTM system. */
     xy.x = xy.x * UTMScaleFactor + 500000.0;
     xy.y = xy.y * UTMScaleFactor;
     if (xy.y < 0.0)
         xy.y += 10000000.0;
 }

 /*
 * UTMXYToLatLon
 *
 * Converts x and y coordinates in the Universal Transverse Mercator
 * projection to a latitude/longitude pair.
 *
 * Inputs:
 *    x - The easting of the point, in meters.
 *    y - The northing of the point, in meters.
 *    zone - The UTM zone in which the point lies.
 *    southhemi - True if the point is in the southern hemisphere;
 *               false otherwise.
 *
 * Outputs:
 *    latlon - A 2-element array containing the latitude and
 *            longitude of the point, in radians.
 *
 * Returns:
 *    The function does not return a value.
 *
 */
 void UTMXYToLatLon (double x, double y, int zone, bool southhemi, WGS84Corr &latlon)
 {
     double cmeridian;

     x -= 500000.0;
     x /= UTMScaleFactor;

     /* If in southern hemisphere, adjust y accordingly. */
     if (southhemi)
         y -= 10000000.0;

     y /= UTMScaleFactor;

     cmeridian = UTMCentralMeridian (zone);
     MapXYToLatLon (x, y, cmeridian, latlon);
 }

 #endif //__COORCONV_H__

然后用MFC写了一个类似的对话框程序:

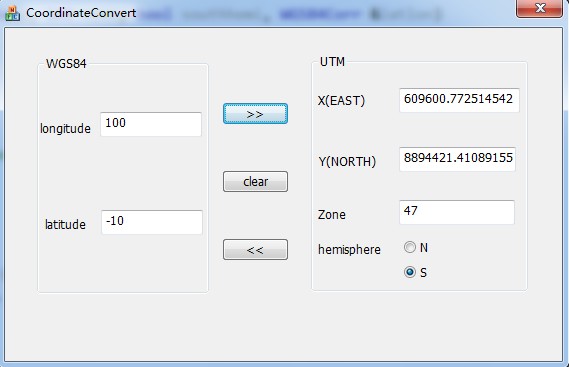
全部的源代码:

http://files.cnblogs.com/wb-DarkHorse/CoordinateConvert.rar

RERERENCE:

1 http://home.hiwaay.net/~taylorc/toolbox/geography/geoutm.html      网页版demo

2 http://www.mogoo.org/fang/?p=65   一位博客里面的，用Java写的

3 http://en.wikipedia.org/wiki/Universal_Transverse_Mercator_coordinate_system  wiki的介绍，公式都写的很清楚，不多说

4 http://my.oschina.net/lidayong/blog/59869  一位博客里的，用c#写的

5 http://www.zhdzch.com/xxyd/chzs/200904/522.html  比较清楚的介绍，用VB写的

下面是国外的几篇资料：

http://www.movable-type.co.uk/scripts/latlong-vincenty-direct.html 根据经纬度求距离

http://www.ngs.noaa.gov/PUBS_LIB/inverse.pdf 对应上面链接的文章

http://trac.osgeo.org/proj/ 一个开源的地图投影库