FFT入门

这篇文章会讲讲FFT的原理和代码。

先贴picks博客（又名FFT从入门到精通）：http://picks.logdown.com/posts/177631-fast-fourier-transform

首先FFT是干嘛用的？

额其实在oi中它就是一个用来算“快速卷积”的东西。

卷积是啥？

给定两个数组a、b，求数组c使得：

for(int i=0;i<n;i++)
    for(int j=0;j<n;j++)
        if(i+j<n) c[i+j]+=a[i]*b[j];

这就叫做长度为n的“卷积”。

正常模拟是O(n^2)的，这时候我们就可以用FFT来加速到O(nlogn)！

我们发现，如果我们令a[i]为x^i的系数，那么a、b就可以表示为一个多项式，c就可以被表示为这两个多项式的乘积。

首先我们可以发现，我们对于一个n次多项式，可以用一个多项式的形式来表示它，也可以找到n个位置的值，这样也可以唯一确定这个多项式。

所以我们就初步有了一个思路，我们找到a、b在n个点处的取值，乘在一起，搞回去确定c的多项式形式。

为了和谐，我们一般令n为2的次幂。（注意）

关于这个东西一般有两种写法，一般被称为复数FFT和NTT。

先讲NTT好了......

假设a、b都是整系数多项式，然后模数P十分刺激，满足P是质数，$2^k|P-1$且$2^k>n$时，我们就可以使用NTT。

然后你还要知道原根的有关概念...简单来说就是原根的次幂在模P意义下循环节为$\varphi(P)$，对于素数来说就是P-1。

这里就说一点，998244353的原根是3...

设g为P的原根，那么我们令$\omega_n=g^{\frac{P-1}{n}}$，可以发现：

$\omega_{2n}^{2m}=\omega_{n}^m$，$\omega_{2n}^m=-\omega_{2n}^{m+n}$。（确实挺显然的）

那么我们取$\omega_n^k$，其中k∈{0...n-1}，作为n个点，如何算出这n个点处的取值呢？

我们假设偶次项提出来作为a0，奇次项提出来作为a1。

（例如1+2x+3x^2+4x^3，偶次项提出来为1+3x，奇次项提出来为2+4x，注意这里的次数也要相应改变）

那么我们可以发现

所以我们可以用a0和a1的点值表示算出a的点值表示。

T(n)=2T(n/2)+O(n)，由主定理复杂度为O(nlogn)。

接下来转回去的话，由于某种奇怪的性质（详细证明可以看picks博客），我们只要用$\omega_{n}^{-m}$代替原来的$\omega_n^{m}$，带进去，最后除以n就行了。即把那一堆$\omega$翻转一下。

当然如果你真这样瞎搞常数似乎真的挺大的，事实上有一些更靠谱的做法，上图：

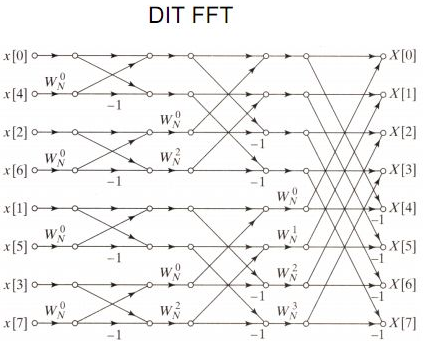
开始我们把输入的数二进制位翻转，就可以得到左边，然后按这个图上进行蝶形运算（就是刚才那两个公式）就可以算出结果了。

额复数FFT更加简单。

我们令$\omega_{n}$为单位根，即满足$x^n=1$的复数，它可以看做复平面上x轴正方向绕逆时针方向旋转$\frac{2\pi}{n}$的复数。所以$\omega_n=cos(\frac{2\pi}{n})+sin(\frac{2\pi}{n})i$。

听起来十分靠谱...但是这种东西毕竟自己瞎写的话常数实在太大了...

下面这个是n+e的NTT模板，有改动，uoj34：

#include <iostream>
#include <stdio.h>
#include <math.h>
#include <string.h>
#include <time.h>
#include <stdlib.h>
using namespace std;
#define ll long long
ll MOD=998244353;
ll w[2][666666];
ll qp(ll a,ll b)
{
    ll ans=1;
    while(b)
    {
        if(b&1) ans=ans*a%MOD;
        a=a*a%MOD; b>>=1;
    }
    return ans;
}
int K;
void fftinit(int n)
{
    for(K=1;K<n;K<<=1);
    w[0][0]=w[0][K]=1;
    ll g=qp(3,(MOD-1)/K); //3是原根
    for(int i=1;i<K;i++) w[0][i]=w[0][i-1]*g%MOD;
    for(int i=0;i<=K;i++) w[1][i]=w[0][K-i];
}
void fft(int* x,int v)
{
    for(int i=0,j=0;i<K;i++)
    {
        if(i>j) swap(x[i],x[j]);
        for(int l=K>>1;(j^=l)<l;l>>=1);
    }
    for(int i=2;i<=K;i<<=1)
    {
        for(int j=0;j<K;j+=i)
        {
            for(int l=0;l<i>>1;l++)
            {
                ll t=(ll)x[j+l+(i>>1)]*w[v][K/i*l]%MOD;
                x[j+l+(i>>1)]=(x[j+l]-t+MOD)%MOD;
                x[j+l]=(x[j+l]+t)%MOD;
            }
        }
    }
    if(!v) return;
    ll rv=qp(K,MOD-2);
    for(int i=0;i<K;i++) x[i]=x[i]*rv%MOD;
}
int N,M,a[666666],b[666666],c[666666];
int main()
{
    scanf("%d%d",&N,&M);
    ++N; ++M; int t=N+M-1;
    for(int i=0;i<N;i++) scanf("%d",a+i);
    for(int i=0;i<M;i++) scanf("%d",b+i);
    fftinit(t); fft(a,0); fft(b,0);
    for(int i=0;i<K;i++) c[i]=(ll)a[i]*b[i]%MOD;
    fft(c,1);
    for(int i=0;i<t;i++) printf("%d ",c[i]);
}