Day 1 下午

POINT 1 贪心

每一步都取当前的最优解的思想；一般来说符合直观思路，需要严格的证明；OI中使用多个错误的贪心策略进行加成有时会有良好的效果

例一
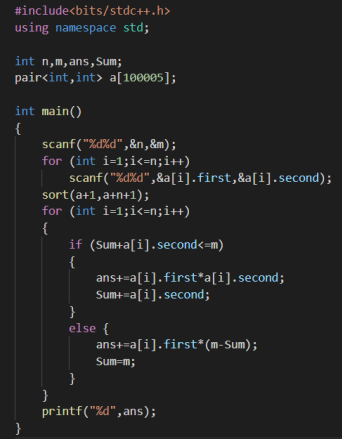
给定N个农民，第i个农民有Ai单位的牛奶，单价Pi
现在要求从每个农民手中购买不超过Ai单位，总共M单位的牛奶。求最小花费 
题解：

将将所有农民按单价排序，能取就取即可

例二
给定n个物品，第i个物品有大小li，要求将这些物品装进容积为L的箱子里，每个箱子至多放两个物品，求最少所需箱子数。

1 ≤ n ≤ 10⁵

题解:

将物品从大到小排序考虑当前的最大物品，假设能与最小值凑成一对，就凑成一对
 
否则必然不存在一个物品能与他凑成一对，因此单列用双指针维护这个过程即可

例三
有n个物品，每个物品有属性Ai和Bi。你需要将他们排成一行 
如果物品i被放在第j个位置，那么会产生代价Ai · (j - 1) + Bi · (n - j)
现在要求总代价的最小值
1 ≤ n ≤ 10⁵

展开式子
得到ans = ΣAi · j - Ai + Bi · n - Bi · j
发现 Bi · n - Ai 是常数，会变化的只有Ai · j - Bi · j
因此按Ai - Bi排序即可

大的放前面，小的放后面

例四
给定n个水龙头，第i个水龙头有最大出水量Ai，且给定一个温度值ti。

定义一次出水得到的温度为Σ(Ai *ti)/Σ(Ai) ，给定一次出水得到的温度T，求最大总出水量。

如果得不到该温度，输出0
1 ≤ n ≤ 2 * 10⁵, 0 ≤ Ai, ti ≤ 10⁶

题解：
先把ti减去T,然后按照t排序
把数组分成两块,一半小于等于0,一半大于0
用贪心的思想,可以发现有一半必须全选,另一半选最靠近T的那些

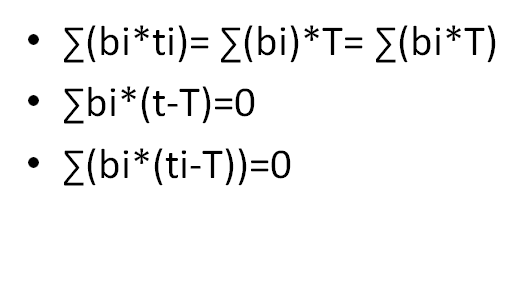
代码：

#include<cstdio>
#include<algorithm>
#include<cstring>

#define N 300005

using namespace std;

int a[N],t[N],i,j,m,n,p,k,id[N],ID[N],sum[N],T;

double ans;

int cmp(int x,int y)
{
        return sum[x]<sum[y];
}

int main()
{
        scanf("%d%d",&n,&T);
        for (i=;i<=n;++i)
        {
                scanf("%d",&a[i]);
        }
        for (i=;i<=n;++i) scanf("%d",&t[i]);
        for (i=;i<=n;++i)
        {
                if (t[i]==T) ans+=a[i];
                else if (t[i]<T) id[++id[]]=i,sum[i]=T-t[i];
                else ID[++ID[]]=i,sum[i]=t[i]-T;
        }
        sort(id+,id+id[]+,cmp);
        sort(ID+,ID+ID[]+,cmp);
        long long suma=,sumb=;
        for (i=;i<=id[];++i)
            suma+=1ll*sum[id[i]]*a[id[i]];
        for (i=;i<=ID[];++i)
            sumb+=1ll*sum[ID[i]]*a[ID[i]];
        if (suma<sumb)
        {
                swap(suma,sumb);
                for (i=;i<=n;++i) swap(ID[i],id[i]);
        }
        for (i=;i<=ID[];++i) ans+=a[ID[i]];
        for (i=;i<=id[];++i)
            if (1ll*sum[id[i]]*a[id[i]]>=sumb)
            {
                    ans+=.*sumb/sum[id[i]];
                    break;
            }
            else
            {
                    ans+=a[id[i]];
                    sumb-=1ll*sum[id[i]]*a[id[i]];
            }
        printf("%.10lf\n",ans);
}

证明:
假设负数集里面还有一些没选,正数集里还有数剩余
那么我们就可以把他们凑出一个0出来,直到某一边用完为止.证毕.

所以就可以直接贪心了

例五
有n个闹钟，第i(1 ≤ i ≤ n)个闹钟将在第ai(1 ≤ ai ≤ 10⁶)分钟鸣响，鸣响时间为一分钟。当在连续的m分钟内，有至少k 个闹钟鸣响，则会被叫醒。

现要求关闭一些闹钟，使得在任意连续的m分钟内，鸣响的闹钟数量恒小于k。

题解：

一个直观的想法是，我们按照重叠最多的顺序排序，但是这样是有问题的，毕竟如果这么一排，就会导致左右两边分开，反而会使情况更糟。

但是如果我们从左往右扫就不一样了。只要碰到会吵醒的情况，我们就弹出，这样能够保证区间是连续的。

并且，由于区间一定会出现问题，所以我们不能就此放置不管我们选择最右面的关闭，因为这样会让剩余的能关的更少

POINT 2 二分

二分的思想
给定一个单调的函数/数组,给定一个值，求这个值是否存在，或者找到这个值应当存在的位置

由于数组有序，不妨认为他单调递增
假设Ai > x,则必然有∀j > i, Aj > x
假设Aj < x,则必然有∀j < i, Aj < x
二分的原理就是每次在待定区间中选择mid。
必然可以确定一边是没有意义的。每次问题的规模缩小 1/2
因此复杂度为O(logN)

寻找<=x的第一个位置

如果两次二分找到的中点一样的话，就说明已经二分完了

#include<cstdio>
#include<algorithm>
#include<cstring>

#define N 300005

using namespace std;

int i,j,m,n,p,k,a[N],x;

int check(int x)
{
        int i,cnt=;
        for (i=;i<=n;++i) if (a[i]-a[i-]>x) return ;
        for (i=;i<n;)
        {
                for (j=i;j<=n&&a[j]-a[i]<=x;++j);
                ++cnt;
                i=j-;
        }
        if (cnt<=m) return ;
        return ;
}

int main()
{
        scanf("%d%d",&n,&m);
        for (i=;i<=n;++i) scanf("%d",&a[i]);
        sort(a+,a+n+);
        int l=,r=(int)1e9,mid=;
        while ((l+r)>>!=mid)
        {
               mid=(l+r)>>;
               if (check(mid)) r=mid;
               else l=mid;
        }
        printf("%d\n",r);
}

最后是答案是存在变量L中

注意一定要是单调序列

二分答案

顾名思义，就是对答案进行二分
对于某些要求“满足某条件的最小值”类的问题，对答案进行二分，假设答案不超过mid，则问题变为“满足某条件且某值不超过mid”的判定性问题。
常用于最大值最小化类问题。

在二分答案之后往往需要一个贪心策略。

例一
一条河上有n个石子排成一条直线，第i个石子距离河岸xi。一只年长的青蛙想要从岸边(x=0处)到达第n个石子上（其实是对岸）。这只青蛙实在是太年长了，所以最多只能

跳m次，而且他希望他这些次跳跃中距离最远的那次距离尽可能的短。请你帮他求出这个最远距离最短能是多少。

1 ≤ m ≤ n ≤ 10⁵

最小化：最大的跳跃距离
二分答案：设答案为mid,则问题变为：
n个石子，只能跳m次，每次跳远距离不能超过mid，问是否可行。

或者n个石子，每次最远距离不超过mid，问最少跳多少次（然后和m比较即可）。

贪心策略：每次跳的尽量远即可

二分O(logN)*贪心O(N)=O(NlogN)

先检查是否能跳的过去

再让他在不超过最远距离的情况下多跳

如果他跳的步数不大于m就可行

例二
给定n个物品，每个物品有属性Ai和Bi。要求在其中选择k个物品，使得选择的物品，的sum(A)/sum(B)尽可能大。

贪心：选Ai/Bi最高的k个物品?
反例：
3 2
1000 10
1000 100
1 1
除了最优的物品一定会选之外 可以考虑选择Bi非常小的物品， 减小对性价比的影响。此时物品3比物品2更优。

二分答案
假设sum(Ai)/sum(Bi) >= mid
则：sum(Ai) - mid * sum(Bi) >= 0
即：sum(Ai-mid*Bi) >= 0
将Ai-mid*Bi作为第i个物品的权值，问题变为能否选k个物品使得权值和大于0.此时贪心选择权值最大的k个物品即可。
二分O(logN)* 排序O(NlogN) = O(Nlog 2N)

二分是对一个单调的函数进行的操作
那么我们有没有办法对一个单峰的函数进行操作呢？
求一个单峰函数的极值点

三分函数

三分

发现共性：l,r中值较小的那一段一定会被舍去严格的实现每次都能缩小问题的 1/3

事实上我们取两次mid会好写很多，只是常数问题

#include<cstdio>
#include<algorithm>
#include<cstring>

#define N 500005

using namespace std;

int i,j,m,n,p,k,a[N],ty,x;

long long b[N];

double check(int x)
{
        return .*(b[x-]+a[n])/x;
}

int main()
{
        scanf("%d",&m);
        for (;m--;)
        {
                scanf("%d",&ty);
                if (ty==)
                {
                        scanf("%d",&x);
                        a[++n]=x;
                        b[n]=b[n-]+x;
                }
                else
                {
                        int l=,r=n;
                        while (r-l>)
                        {
                            int len=(r-l+)/,mid1=l+len,mid2=mid1+len;
                            if (check(mid1)<check(mid2)) r=mid2;
                            else l=mid1;
                        }
                        double ans=;
                        for (i=l;i<=r;++i) ans=max(ans,a[n]-check(i));
                        printf("%.10lf\n",ans);
                }
        }
}

例一
初始有一个为空的集合,要求支持两种操作
1.不断向集合中插入一个数，且这个数比集合中所有数都大
2.在集合中找一个子集，使得找到的子集S中的最大值减去子集S中元素的平均值的差最大，并输出这个差

操作数≤ 500000

最大值肯定要选，可以自己证明一下

然后使其他数尽可能小

如何选取子集？
最后插入的这个数是一定要选的，然后再选小的数，就是一个最大数加上几个用来拉低平均值的小数构成了所需子集

小数一定是从最小值开始连续增加使平均值减小，直到达到一个临界点，再增加小数就会使平均值增大，易知这是一个单峰函数

因此考虑三分选多少小数即可

题解：

让上线稍微大一些

check：取前k个的和

(前x-1小的数+a[n])/x

main：

其他的三分就是更改check函数

分治的思想
将一个问题划分成若干个（一般都是分成俩）子问题
分别解决每个子问题后（也可能是前，还可能一前一后之类
的）
将各个子问题组合起来得到原问题的答案。

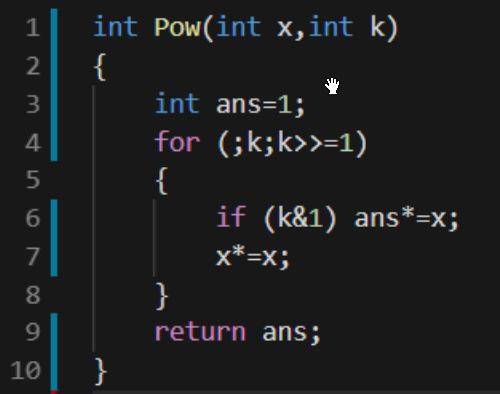
快速幂
如何快速计算X ^k？

我们将k进行二进制拆分。
比如我们需要计算X 11即我们需要计算X 20+21+23
因此我们只需要计算logk 次即可

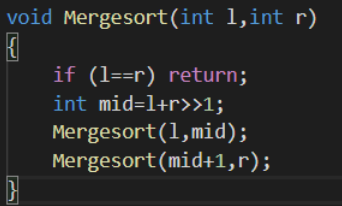
归并排序
基本思想：先将整个数组分成两个部分，分别将两个部分排好序，然后将两个排好序的数组O(n)合并成一个数组。

我们将问题分为两个阶段：分、治

分
对于每个长度> 1的区间，拆成两个[l, mid]区间和[mid + 1, r]区间

直接递归下去

治
我们认为在处理区间[l,r]时，已经有[l,mid]和[mid+1,r]内分别有序

这一次的操作就是合并两个有序序列，成为一个新的长有序序列

用两个指针分别指向左右分别走到哪了即可

比较两个指针指向的值

复杂度O(nlogn)是一个严格的算法

逆序对
给定一个1 ∼ n的排列，求逆序对数量。
1 ≤ n ≤ 10⁵
逆序对：对于1 ≤ x < y ≤ n, 若A[x] > A[y]，则称(x,y)为一个逆序对。

题解
首先显然我们枚举x,y可以做到O(N2)
分治：
假设当前问题 Work(l,r) 是求l到r区间内的逆序对数量。
讨论所有(x,y)可能在的位置：
l ≤ x < y ≤ mid ：子问题Work(l,mid)
x ≤ mid < y ： ？？？
mid + 1 ≤ x < y ≤ r ：子问题Work(mid+1,r)

对于每个mid右边的数，我们要找到mid左边有多少比它大的数。

1) 对左侧排序，右侧在左侧上二分即可。 总时间复杂度O(nlog2n)

2) 归并排序：
对于数组A和数组B的归并过程，每当我们将B中的元素取出时：
说明A中最小的元素比该元素大：说明A中所有元素比该元素大：说明 答案+=A.size()

归并过程时间复杂度O(n)，总时间复杂度O(nlogn)。

例二
有一个序列，初始时只有一个数n
对于序列中每一个> 1的数，拆分成三个数n/2,n%2,n/2并替换原数。
直到序列中没有> 1的数为止
查询最终序列中[l, r]中有多少1
0 ≤ n < 2⁵⁰, 0 ≤ r - l ≤ 10⁵

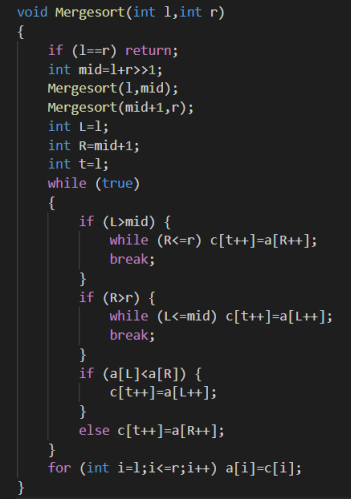
平面最近点对
给定二维平面上的N个点，求任意两点间的最近距离（欧几
里得距离）。
1 ≤ n ≤ 10⁵

题解
不妨按照x坐标排序。对于区间[l,r]，我们将其分成mid左右
两个部分。
两个点都在左侧：子问题Work(l,mid)
两个点都在右侧：子问题Work(mid+1,r)
两个点一个在左侧，一个在右侧 ：

不妨按照x坐标排序。对于区间[l,r]，我们将其分成mid左右
两个部分。
两个点都在左侧：子问题Work(l,mid)
两个点都在右侧：子问题Work(mid+1,r)
两个点一个在左侧，一个在右侧：
重点考虑第三种情况

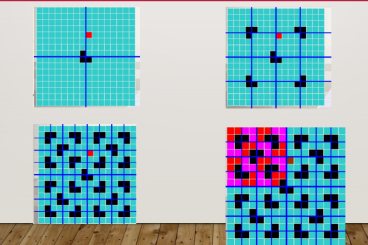
不妨假设左右两个子问题的答案为ans。则我们只需要考虑
分界线两边距离不超过ans以内的点即可。

不妨假设左右两个子问题的答案为ans。则我们只需要考虑
分界线两边距离不超过ans以内的点即可。

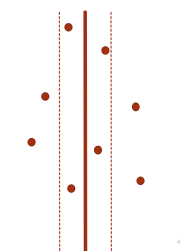
不妨假设左右两个子问题的答案为ans。则我们只需要考虑
分界线两边距离不超过ans以内的点即可。

对于每个点，可能和它距离不超过ans的点坐标范围
横坐标：[mid-ans,mid+ans]
纵坐标：[y-ans,y+ans]

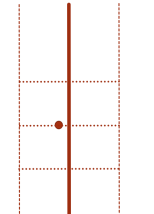
每个小正方形内点数不可能超过一个（因为任意两点距离不
低于ans）。故总点数不超过6个。除去该点自身，该点至多
需要和其他6个点求距离。
故该部分复杂度不超过O(n)。实现时可以直接对所有点按
照y坐标排序，O(n log2 n)，或者使用归并排序的技巧，直
接O(n log n)即可。