BST讲解

BST

　　第一步，什么是BST，所谓BST就是满足一种特定性质的二叉树，这个性质一般情况是当前节点的权值比他的左子树的所有点的权值大，比他的右子树的所有点的权值小，满足这样性质的二叉树就称为BST，下面给一个例子。如图，就是一棵BST，显而易见，我们可以看出他的中序遍历是用点权从小到大排序之后的顺序。讲到这里，就会有人发问，如果有多个相同权值的点怎么办？定义里没有提到相同啊。这个问题很好回答，我们可以在维护BST的同时，维护一个数组，用来存当前节点的权值出现几次，输出时特殊处理就好啦（下图）。这就是BST，是不是很简单？代码实现也比较简单。

　

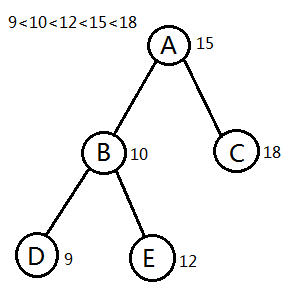
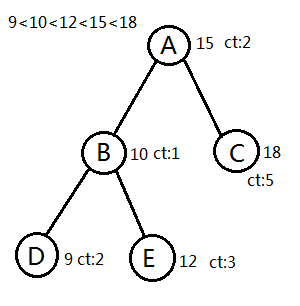
　　建树：我们想添加一个节点时，就可以从根节点开始寻找，每一次和当前节点相比，如果小于则递归左子树，如果大于则递归右子树，如果找到权值和他相等的点，ct直接加一就可以了，如果没有找到，我们就可以找到最末尾的点，直接在其后面挂上一个新的节点，代表这个值，ct=1。

 void add(int &p,int number)
 {
     if(!p)
     {
         p=++idx;ct[p]=;
         num[p]=number;
         return;
     }
     if(num[p]<number) add(rson[p],number);
     else add(lson[p],number);
 }
 //ct[p]代表p号节点出现的次数
 //num[p]代表p号节点的权值
 //lson[p]代表p号节点的左儿子的编号
 //rson[p]代表p号节点的右儿子的编号

建树

　　输出：我们只需要写一个中序遍历就可以了，十分简单。

 void put(int p)
 {
     if(lson[p]) put(lson[p]);
     for(int i=;i<=many[p];i++)
         printf("%d\n",val[p]);
     if(rson[p]) put(rson[p]);
 }
 //many[p]记录p号节点出现的次数
 //lson[p]记录p号节点的左儿子的编号
 //rson[p]记录p号节点的右儿子的编号
 //val[p]记录p号节点的权值

输出

　　第一次写BST的同学可以先写一下排序的题目，比如JDOJ1068排序和洛谷P1177，联系一下。

　　练习过后，可能有人会问，为什么过不去？TLE？这个问题实际上很好解释，如果插入时候是按照顺序插入的，就会变成一个链，这个很好理解，画一画就知道了。当退化成链的时候，时间复杂度就会退化成O(n^2)，自然会TLE。

　　在这里我推荐两种做法，第一种是针对读入的顺序改变之后对答案没有影响的题，我们可以用random_shuffle()把数组打乱，这样的话P1177就可以轻松过了。

　　第二种就是Treap。这种做法可以写读入的顺序改变之后对答案有影响的题，具体讲解请看下一篇博客。