bzoj千题计划108：bzoj1018: [SHOI2008]堵塞的交通traffic

http://www.lydsy.com/JudgeOnline/problem.php?id=1018

关键点在于只有两行

所以一个2*m矩形连通情况只有6种

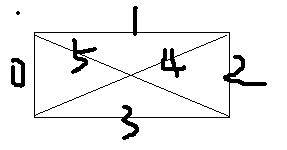
编号即对应代码中的a数组

线段树维护

用b数组表示 节点第0/1行的最右一列是否连接了右边

来 辅助 节点的合并

查询

对两个点位于矩形的位置分4种情况讨论

两点是否联通，要考虑四种情况

（以两个位置是矩形左上角和右上角为例）

1、直接联通，线段树的节点包含了这种情况，直接判断

2、

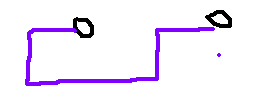
3、

4、

后三种情况需要再查询[1,l]和[r,n]的再合并

边界的处理：

（叶子节点只有一列）

只有一列的状态1和3 全部是true

如果是竖着联通，同时更新状态0和2，4和5

如果是横着联通，

第1行，如果最后一列可以往外合并，更新状态5

第2行，如果最后一列可以往外合并，更新状态4

#include<cstdio>
#include<cstring>
#include<iostream>
#include<algorithm>

#define ok { puts("Y"); continue; }

using namespace std;

#define N 100001

int L[N<<],R[N<<];

struct node
{
    bool a[],b[];
    void clear() { memset(a,false,sizeof(a)); memset(b,false,sizeof(b)); }
    node operator + (node p) const
    {
        node tmp;
        tmp.clear();

        tmp.a[]=a[];
        tmp.a[]|=a[]&&a[]&&b[]&&b[]&&p.a[];
    //    cout<<tmp.a[0];
        tmp.a[]=a[]&&b[]&&p.a[];
        tmp.a[]|=a[]&&b[]&&p.a[];
    //    cout<<tmp.a[1];
        tmp.a[]=p.a[];
        tmp.a[]|=p.a[]&&p.a[]&&b[]&&b[]&&a[];
    //    cout<<tmp.a[2];
        tmp.a[]=a[]&&b[]&&p.a[];
        tmp.a[]|=a[]&&b[]&&p.a[];
    //    cout<<tmp.a[3];
        tmp.a[]=a[]&&b[]&&p.a[];
        tmp.a[]|=a[]&&b[]&&p.a[];
    //    cout<<tmp.a[4];
        tmp.a[]=a[]&&b[]&&p.a[];
        tmp.a[]|=a[]&&b[]&&p.a[];
    //    cout<<tmp.a[5];
        tmp.b[]=p.b[]; tmp.b[]=p.b[];

        return tmp;
    }
};

node tr[N<<];

void read(int &x)
{
    x=; char c=getchar();
    while(!isdigit(c)) c=getchar();
    while(isdigit(c)) { x=x*+c-''; c=getchar(); }
}

void build(int k,int l,int r)
{
    L[k]=l; R[k]=r;
    if(l==r)
    {
        tr[k].a[]=tr[k].a[]=true;
        return;
    }
    int mid=l+r>>;
    build(k<<,l,mid);
    build(k<<|,mid+,r);
}

void change(int k,int pos,bool ty,int line,bool how)
{
    if(L[k]==R[k])
    {
        if(!ty)
        {
            if(line==)
            {
                tr[k].b[]=how;
                if(tr[k].b[] && tr[k].a[]) tr[k].a[]=true;
                else if(!tr[k].a[]) tr[k].a[]=false;
            }
            else
            {
                tr[k].b[]=how;
                if(tr[k].b[] && tr[k].a[]) tr[k].a[]=true;
                else if(!tr[k].a[]) tr[k].a[]=false;
            }
        }
        else
        {
            tr[k].a[]=tr[k].a[]=how;
            tr[k].a[]=tr[k].a[]=how;
        }
        return;
    }
    int mid=L[k]+R[k]>>;
    if(pos<=mid) change(k<<,pos,ty,line,how);
    else change(k<<|,pos,ty,line,how);
    tr[k]=tr[k<<]+tr[k<<|];
}

node query(int k,int l,int r)
{
    if(L[k]>=l && R[k]<=r) return tr[k];
    int mid=L[k]+R[k]>>;
    if(r<=mid) return query(k<<,l,r);
    if(l>mid) return query(k<<|,l,r);
    node ll=query(k<<,l,r),rr=query(k<<|,l,r);
    return ll+rr;
}

int main()
{
//    freopen("bzoj_1018.in","r",stdin);
//    freopen("bzoj_1018.out","w",stdout);
    int n; read(n);
    build(,,n);
    char c[];
    int lx,ly,rx,ry;
    int cnt=;
    while(scanf("%s",c)!=EOF)
    {
        if(c[]=='E') return ;
        read(lx); read(ly); read(rx); read(ry);
        if(ly>ry) swap(lx,rx),swap(ly,ry);
        if(c[]=='O' || c[]=='C')
        {
            if(lx==rx) change(,ly,,lx,c[]=='O');
            else change(,ly,,lx,c[]=='O');
        }
        else
        {
            node tmp=query(,ly,ry);

            if(ly==ry && tmp.a[]) ok
            else if(ly!=ry)
            {
                if(lx== && rx== && tmp.a[]) ok
                if(lx== && rx== && tmp.a[]) ok
                if(lx== && rx== && tmp.a[]) ok
                if(lx== && rx== && tmp.a[]) ok
            }
            node l=query(,,ly);
            node r=query(,ry,n);
            if(lx== && rx==)
            {
                if(l.a[]&&tmp.a[]) ok
                if(r.a[]&&tmp.a[]) ok
                if(l.a[]&&r.a[]&&tmp.a[]) ok
            }
            else if(lx== && rx==)
            {
                if(l.a[]&&tmp.a[]) ok
                if(r.a[]&&tmp.a[]) ok
                if(l.a[]&&r.a[]&&tmp.a[]) ok
            }
            else if(lx== && rx==)
            {
                if(l.a[]&&tmp.a[]) ok
                if(r.a[]&&tmp.a[]) ok
                if(l.a[]&&r.a[]&&tmp.a[]) ok
            }
            else
            {
                if(l.a[]&&tmp.a[]) ok
                if(r.a[]&&tmp.a[]) ok
                if(l.a[]&&r.a[]&&tmp.a[]) ok
            }
            puts("N");
        }
    }
}

1018: [SHOI2008]堵塞的交通traffic

Time Limit: 3 Sec  Memory Limit: 162 MB
Submit: 3852  Solved: 1265
[Submit][Status][Discuss]

Description

　　有一天，由于某种穿越现象作用，你来到了传说中的小人国。小人国的布局非常奇特，整个国家的交通系统可
以被看成是一个2行C列的矩形网格，网格上的每个点代表一个城市，相邻的城市之间有一条道路，所以总共有2C个
城市和3C-2条道路。 小人国的交通状况非常槽糕。有的时候由于交通堵塞，两座城市之间的道路会变得不连通，
直到拥堵解决，道路才会恢复畅通。初来咋到的你决心毛遂自荐到交通部某份差事，部长听说你来自一个科技高度
发达的世界，喜出望外地要求你编写一个查询应答系统，以挽救已经病入膏肓的小人国交通系统。 小人国的交通
部将提供一些交通信息给你，你的任务是根据当前的交通情况回答查询的问题。交通信息可以分为以下几种格式：
Close r1 c1 r2 c2：相邻的两座城市(r1,c1)和(r2,c2)之间的道路被堵塞了；Open r1 c1 r2 c2：相邻的两座城
市(r1,c1)和(r2,c2)之间的道路被疏通了；Ask r1 c1 r2 c2：询问城市(r1,c1)和(r2,c2)是否连通。如果存在一
条路径使得这两条城市连通，则返回Y，否则返回N；

Input

　　第一行只有一个整数C，表示网格的列数。接下来若干行，每行为一条交通信息，以单独的一行“Exit”作为
结束。我们假设在一开始所有的道路都是堵塞的。我们保证 C小于等于100000，信息条数小于等于100000。

Output

　　对于每个查询，输出一个“Y”或“N”。

Sample Input

2
Open 1 1 1 2
Open 1 2 2 2
Ask 1 1 2 2
Ask 2 1 2 2
Exit

Sample Output

Y
N

HINT

题解：JudgeOnline/upload/201604/sol(4).rar