克拉默法则（Cramer's Rule）的证明

克拉默法则：

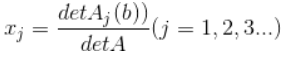
先说一下为什么要写这个，作为一个大一新生，必须要学的就包括了线性代数，而且线性代数等数学知识对计算机专业也有很大帮助。但是在学习过程中遇到一个讲解的不清楚的知识点（Cramer's Rule），于是上网查询，但是出乎意料的是网上的证明方法都复杂且大多数都是用验证法，这对于数学的学习是及其没有帮助的，我作为一个数学爱好者就开始探索了。我坚信所有成立的公式都可以有一个显式的解读，不能读出来总是你打开的方式不对。

一、引理（行列式的性质）（参考书籍：Introduction to Linear Algebra,Gilbert Strang, Wellesley-Cambridge Press, ISBN：0980232775, 9780980232776, 2016.）

1. 单位矩阵的行列式为1.
2. 把矩阵A的行a加到矩阵A的行b，矩阵行列式不变（a≠b）.
3. 对角矩阵的行列式等于对角线元素乘积.
4. detAB=(detA)(detB).//两个矩阵乘积的行列式等于两个矩阵的行列式的乘积.

以上引理均为转述，并非原文，有需要请查阅原书。

二、证明（注意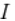表示单位矩阵，同某些书的 E）

第一步，将其化为它真正表达的意思

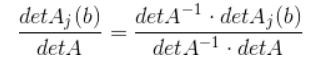
第二步，

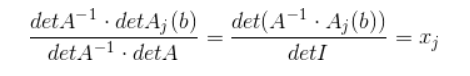
det（I）=1，没错这个就证明结束了。

可能最后一步有人没有看懂，我解释一下。

我们用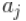(j=1,2,3....n)，来表示A的每一列,用

稍微看一下矩阵乘法，我们明白

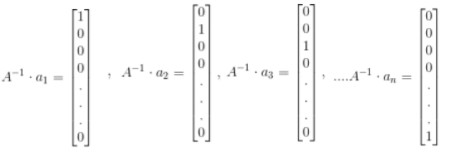
即，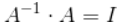

而显然

也就是

而用引理2（把矩阵A的行a加到矩阵A的行b，矩阵行列式不变（a≠b）.）可以将第j列除第j行以外的所有值减为0，

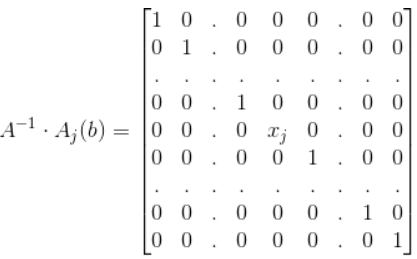
根据引理三（对角矩阵的行列式等于对角线元素乘积.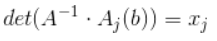），.(或者也可以利用提出一行的公因子)

证毕。

引理的证明请看书或者自行百度。

如果以上结果有误，请联系我。

如果想要我证明其它公式的，请联系我。

如果有同样喜欢数学的，也可以一起探讨。