MIT-线性代数笔记（1-6）

学习目录

第 01 讲 行图像和列图像

第 02 讲 矩阵消元

第 03 讲 矩阵的乘法和逆矩阵

第 04 讲 矩阵的LU 分解

第 05 讲 转置、置换和空间

第 06 讲 列空间和零空间

第 07 讲 求解 Ax=0:主变量，特解

第 08 讲 求解Ax=b：可解性与解的结构

第 09 讲 线性相关性、基、维数

第 10 讲 四个基本子空间

第 11 讲 矩阵空间、秩1矩阵和小世界图

第 12 讲 图和网络

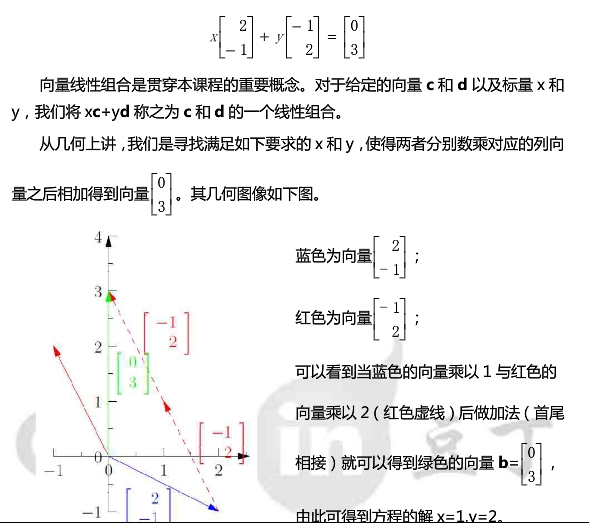
第 01 讲 行图像和列图像

第 02 讲 矩阵消元

　　只要矩阵可逆，均可通过消元法求得 Ax=b 的解

　　若此处

　　

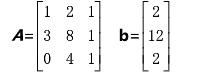
　　高斯消元法：

　　对方程组中某个方程进行时的那个的数乘和加减，将某一未知系数变为零，来削弱未知数个数

　　矩阵左上角 1 为“主元一”

　　① 用消元法将除了第一行，消除其他行中的主元一

　　

　　主元不能为0，如果恰好消元至某行，0出现了主元的位置，应当通过与下一行进行“行交换”，使得非零数字出现在主元位置上；如果此时下方没有对等位置上非零，则消元终止并证明此矩阵不可逆，且线性方程组没有唯一解

回代

　　应用增光矩阵，对等式右侧做同样运算

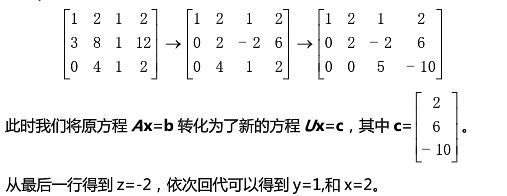
第 03 讲 矩阵的乘法和逆矩阵

1）标准乘法（行*列）

2）列操作

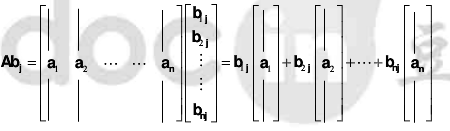
3）行操作

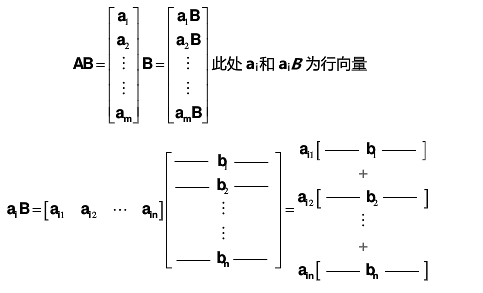
4）分块乘法

　　　　　　

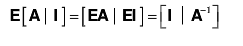
第 04 讲 矩阵的LU 分解

第 05 讲 转置、置换和空间

一、置换矩阵Permutation

置换矩阵：可进行交换的矩阵，是行重新排列了的单位矩阵。注意点：
1）单位矩阵是最基本的置换矩阵。

2）n揭一共有n!个置换矩阵。
3）所有置换矩阵都可逆，而且逆与其转置相等。一个置换矩阵乘以其转置等于单位矩阵。

二、向量空间Vectorspaces，子空间subspaces重点理解向量空间概念，子空间概念

向量空间：

　　表示有很多向量，一整个空间的向量。但并不是任意向量的组合都能成为空间。必须满足一定规则，必须能够进行加法和数乘运算，必须能够进行线性组合，对加法和数乘运算封闭。

向量空间性质（或者说需要满足的规则）：对加法和数乘运算封闭，或者说对线性组合封闭，即所有的空间内的向量线性组合后仍在空间内。

子空间：

　　满足空间规则，但又不需包含所有向量。取某向量空间的部分空间（显然得到的就不是向量空间了），这部分中的向量不管是加法还是数乘，结果依然在此部分空间内，这就是子空间。

　　R2的子空间：1）穿过原点的直线；2）原点；（特别注意，这不是零空间，只能说零向量是R2的子空间）3）R2
　　R3的子空间：1）穿过原点的直线；2）穿过原点的平面；3）原点；（特别注意，这不是零空间）4）R3

第 06 讲 列空间和零空间

如下例子，A的列空间是R4的子空间，记为C(A)，抽象起来：A的列空间由A三个列向量的线性组合组合构成。

这个空间到底是什么样子？它等于整个四维空间吗？

不等于，它只是相当于四维空间的一个较小的空间。
抽象背后的实际目的，都是为了深刻认识Ax=b，Ax=b是否对任意b（右侧向量）都有解？或者说，什么样的b使方程组有解？
Ax=b对任意b并不总有解，因为Ax=b中有四个方程，却只有三个未知数。方程组不总有解，因为3个列向量的线性组合无法充满整个四维空间，因此还有一大堆的b不是这三个列向量的线性组合。

怎样的b，能让方程组有解，什么样的右侧向量有这种性质？什么b让方程组有解？

1）b为零向量。Ax=0总有一个零解
2）b是列向量的线性组合。Ax=b有解，当且仅当右侧向量b属于A的列空间。（列空间包含所有A乘以任意x得到的向量，也就是包含所有有解的b）
列空间是非常核心的内容，它能告诉我何时方程组有解。

更深入一些的问题，以上三个列向量是否线性无关，是否有某个向量并没有起到作用，能否去掉某列，得到同样的列空间？上面的A，其实可以去掉第三列，因为第三列是前两列的和线性组合，我们把前两列称为A的主列。其实，我们同样可以去掉第一列或者第二列，因为他们是其余两列的差线性组合。不过按照惯例，优先考虑靠前的线性无关向量。

求解零空间
一般方法为消元法。但上式的解很容易看出来

怎样描述这个零空间，这里的零空间是R3中穿过原点的一条直线。

如下，考虑另外一个问题，右侧b向量取一个非0向量，此时x有解，（这时x的解不是零空间了），那么所有的x解构成子空间吗？很明显不构成子空间，或者说向量空间。因为很明显0向量不在这个空间内，没有0向量，就不用谈向量空间了（原因很明显，数乘运算中，常数取0时需要满足封闭规则）。

那么它的解是什么？（100），（0-1-1）。。。它实际上是一条不穿过原点的直线（或者在别的更普通的例子中是不穿过原点的平面）

以上两种子空间的总结：

有两种方法构造子空间，其一是通过列的线性组合构造列空间，其二是求解向量必须满足的方程组来构造子空间（通过让x满足特定条件来得到子空间，Ax=0将构造出零空间）