【QAQ的Minecraft】

树套树被QAQ用木斧挖了，只剩二维RMQ了。

题目：

     QAQ最近爱上了一款很平凡的游戏，叫做《Minecraft》。目前游戏更新到了1.12版本，他发现了一条新的指令：/fill x y z X Y Z……,在网络上搜索后，他了解到这条指令的意义是：将坐标为(x,y,z)和(X,Y,Z)两点为对角线的长方体赋值为一种方块。由于他想使用这个指令来建造正方形地板，所以他认为要把z坐标全设置为1，这样就只需要考虑x,y了。他正想用该指令的时候，发现了一个问题：如果他直接执行命令，可能会覆盖地上他的一些可爱的小花花，这是他不愿意的，所以总结来说，你要帮他在地上找到一块面积最大的正方形（输出边长即可）,满足这个正方形不经过任何一朵小花花。

[输入描述]

    输入正整数n,m(1<=n,m<=1000)表示整个场地的大小。接下来输入一个n*m的矩阵，表示地面：1表示空地，0表示有小花花。然后输入询问个数q(q<=1000000)，接下来输入q个询问，每个询问的格式为：(x1,y1,x2,y2)表示询问在以(x1,y1)和(x2,y2)为对角线的矩形中，不经过小花花(花在边上也算经过)的正方形中，边长最大的正方形的边长是多少。

[输出描述]

    输出q个正整数，表示q个询问的答案。

[输入样例]

3 4
1 1 0 1
0 1 1 0
0 1 1 0
5
1 1 2 3
2 1 3 2
3 2 3 4
1 1 3 4
1 2 3 4

[输出样例]

1

1

1

2

2

·分析

      可以清晰的发现这是一个需要很多优化的题——因为一看题我们可以敏捷地想到使用二维前缀来维护边长最大矩形，然后依仗上述预处理暴力回答询问，最后发现严重超时。

      审视数据范围：n,m<=1000,q<=1000000。可以得到两个不太精确的信息：(1)预处理时间复杂度O(n*n),O(n*n*logn),O(n*n*logn*logn)可以支持(已经是极限了)。(2)对于每个询问必须O(1)或者O(logn)解决。

      先考虑怎样满足询问的时间限制，我们可以使用二维RMQ来达到要求(或者一时想不出来的神奇解法)，但这只是猜想，毕竟还要看看预处理是否满足。

      对于预处理，我们根据上文的经验，原本使用了f[i][j]表示以点(i,j)为右下角的边长最大正方形的边长，其递推方程式容易写出：
    f[i][j]=a[i][j]?min{f[i][j-1],f[i-1][j],f[i-1][j-1]}+1:0

     (a[i][j]表示输入的地图)

     但是这样的预处理有局限性——我们的询问是对于一个二维区间内的正方形，可是单个f[i][j]是对于以(i,j)为右下角的正方形的，这样如果不加以修饰，那么对于一个询问，我们就只有暴力每一个点，即将每个点作为右下角进行一次取值，这样不幸超时。

     因此，我们需要保存一段二维区间的所有f[i][j]值，到时候回答时就可以直接使用了。为了维护一段二维区间的最值，我们首先想一想RMQ(树套树在询问的时候是O((logn)³),无力胜任)，根据一维RMQ的思路:g[k][i]表示以i为终点，长度为2^k的一段区间的最大值，来推广至二维RMQ：g[k1][k2][i][j]表示以(i,j)为右下角，以(i-2^k1,j-2^k2)为左上角的矩形内f的最大值。

     这样，我们的预处理时间复杂度为O(n*n*logn*logn)。询问时间复杂度看上去是O(1)，但是还有一个小问题：

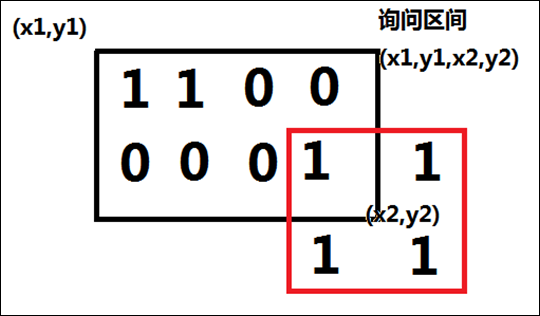
如图，红色的正方形不完全属于询问区间，本不能贡献答案，可是由于我们保存的是f[i][j](图中f[i][j]是以(i,j)为左上角的最大正方形边长)，所以RMQ就会将其作为答案的考虑，这样输出结果为2，实际上是1，就WA了。

     上述问题产生的原因是一个合法正方形(即不覆经过小花花)的一部分在询问区间内(尤其是右下角，因为f[i][j]的定义这样的)，就误将其作为答案考虑。为了避免这种情况，同时注意时间复杂度的保持，怎么做啊？

     首先给出方法：牺牲时间复杂度，使每个询问回答成为(logn),将分出来的logn拿给二分——二分答案，同时这个二分的结果还有一个限制作用，可以用于防止上文的正方形超界的情况，如一个图:

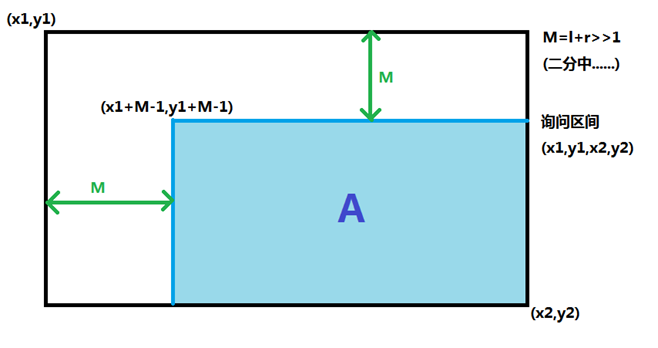
  我们将RMQ的询问区间缩小至A区间。那么就算是遇到了超界的情况，我们也不在意，我们只关注是否最大值大于M即可，举例如图：

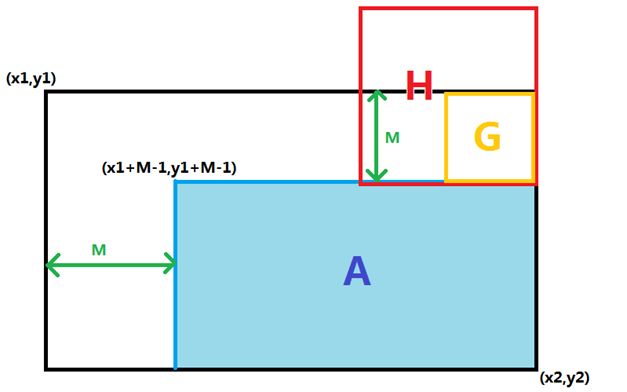
     注意，我们现在找到的答案来自于A中所有的f的最大值，那么就可能会出现图中红色正方形的情况，但是，既然红色的大正方形成立(虽然它不在询问区间内)，那么合法的G正方形则可以作为答案考虑，由于每次二分我们只需要判断是否能够找到边长为M的合法正方形，所以这样我们只需要找到的值大于等于M就可以在check函数中返回True了。本题二分的精髓就在这里完全展现了。

     另外的注意事项，对于询问A矩形的最值，RMQ怎样询问？当然要向一维(一个序列)那样分段考虑啊：

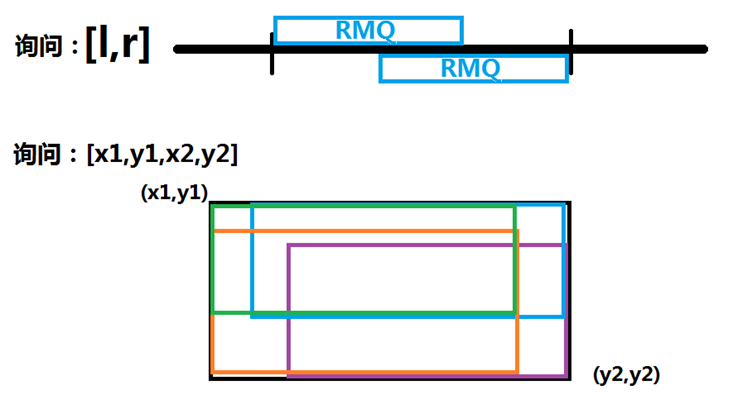
第二幅图有些凌乱，但只要结合一维区间RMQ的思路，二维无非是两两组合。RMQ之所以这样做的根本原因是其区间是固定的，是2^k长度，然而我们询问区间是不定的，所以需要2^k长度去拼接重叠才能达到要求。

     代码说：“我要来！”。

 #include<stdio.h>
 #include<algorithm>
 #define f g[0][0]
 #define go(i,a,b) for(register int i=a;i<=b;i++)
 using namespace std;const int N=;
 int n,m,g[][][N][N],K[<<],D[],q,x,y,X,Y,l,r,M,ans;
 char Getchar()
 {
     static char s[],*p1=s,*p2=s;
     if(p1==p2)p2=(p1=s)+fread(s,,,stdin);return *p1++;
 }
 void Judy(int &w)
 {
     int x=;w=;char c=;
     while(c<''||c>''){if(c=='-')w=-;c=getchar();}
     while(!(c<''||c>''))x=x*+c-'',c=getchar();w=x*w;
 }
 int find(int x1,int y1,int x2,int y2)
 {
     int k1=K[x2-x1+],k2=K[y2-y1+];return max(max(
     g[k1][k2][x2][y2],
     g[k1][k2][x1+D[k1]-][y1+D[k2]-]),max(
     g[k1][k2][x1+D[k1]-][y2],
     g[k1][k2][x2][y1+D[k2]-]));
 }
 int main()
 {
     freopen("square.in","r",stdin);
     freopen("square.out","w",stdout);
     Judy(n);Judy(m);D[]=;go(i,,){D[i]=D[i-]<<;
     go(j,D[i-],D[i]-)K[j]=i-;}

     go(i,,n)go(j,,m)Judy(f[i][j]),f[i][j]?
         f[i][j]=min(f[i-][j-],min(f[i][j-],f[i-][j]))+:;
     go(k,,)go(i,D[k],n)go(j,,m)
         g[k][][i][j]=max(g[k-][][i][j],g[k-][][i-D[k-]][j]);
     go(k,,)go(i,,n)go(j,D[k],m)
         g[][k][i][j]=max(g[][k-][i][j],g[][k-][i][j-D[k-]]);
     go(k1,,)go(k2,,)go(i,D[k1],n)go(j,D[k2],m)
         g[k1][k2][i][j]=max(g[k1][k2-][i][j],g[k1][k2-][i][j-D[k2-]]);

     Judy(q);
     while(q--)
     {
         Judy(x);Judy(y);Judy(X);Judy(Y);ans=;
         int l=,r=min(X-x+,Y-y+);
         while(l<=r)M=l+r>>,find(x+M-,y+M-,X,Y)>=M?ans=M,l=M+:r=M-;
         printf("%d\n",ans);
     }
     return ;
 }//Paul_Guderian

路缓缓流向远方，旷野的天空云彩飞扬，

时光在房间里回荡，我坐着心在歌唱。————汪峰《生命中的一天》