[BZOJ]3243 向量内积(Noi2013)

　　小C做了之后很有感觉的题目之一，但因为姿势不对调了很久。

Description

　　两个d 维向量A=[a1,a2,...,ad]与B=[b1,b2,...,bd]的内积为其相对应维度的权值的乘积和，即：

　　　　　　

　　现有 n 个d 维向量x1,...,xn ，小喵喵想知道是否存在两个向量的内积为k的倍数。请帮助她解决这个问题。

Input

　　第一行包含3个正整数n,d,k，分别表示向量的个数，维数以及待检测的倍数。接下来n行每行有d个非负整数，其中第i行的第j个整数表示向量xi的第j维权值xi,j。

Output

　　包含两个整数，用空格隔开。如果存在两个向量xp,xq的内积为k的整数倍，则输出两个向量的编号p与q（要求p<q）。如果存在多组这样的向量组合，输出其中任意一组即可。若不存在这样的向量组合，则输出两个-1。

Sample Input

　　2 20 2
　　0 0 1 1 1 1 1 0 1 1 1 0 1 0 0 0 1 1 1 1
　　1 0 1 0 1 0 1 1 1 1 0 1 1 1 0 1 1 0 1 0

Sample Output

　　1 2

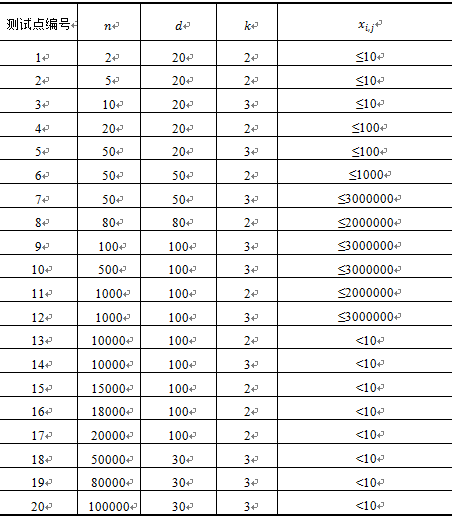
Hint

　　N<=100000，D<=30，K<=3，Xi,j<10。

　　

Solution

　　看见题目后基本能想到的要点：

　　　　①k似乎很小？k=2时答案只可能是0或1，k=3则是0、1和2？

　　　　②向量内积的求和式其实就是矩阵乘法的计算式，两个向量的内积可以看做是1*d和d*1的矩阵相乘。

　　继续深入：

　　　　①可以将题目表示为n*d和d*n的矩阵相乘，得到的n*n的矩阵就是n个向量两两之间的内积，判断n*n矩阵内是否有等于0的元素即可；

　　　　②直接计算和判断明显复杂度爆表，我们考虑将计算和判断部分进行优化：

　　　　　　当k=2时，n*n的矩阵只有一种情况不是我们想要的，那就是除了对角线上的元素，其他都为1——设这样的矩阵为D；

　　　　　　　　　　　设原来的两个矩阵分别为A、B，相乘得到矩阵C；

　　　　　　　　　　　这样我们只需判断C和D是否相等即可，我们当然不会直接判断，这里需要用到一个小技巧。

　　　　　　　　　　　我们考虑随机生成一个n*1的矩阵T来与C、D相乘，判断C*T和D*T是否相等即可。

　　　　　　　　　　　随机次数3~5次基本不会出错，这样我们便将判断成功降到了O(n)。

　　　　　　　　　　　至于计算部分，我们只要按A*(B*T)的顺序就可以O(nd)得到C*T；

　　　　　　　　　　　由于矩阵D是确定的，主对角线O(nd)计算，O(n)再推一遍可以得到D*T。

　　　　　　　　　　　剩下的事情就是找出不相等的一位x，相当于找到了答案的一半（x一定是答案），O(nd)找另一半即可。

　　　　　　当k=3时，我们可以脑补一个2^2≡1(mod 3)，于是考虑将矩阵C、D的每个元素平方（注意不是将矩阵平方！）。

　　　　　　　　　　　这样矩阵D的每个除了主对角线上的元素便都是1了，像k=2那样判断C和D是否相等即可。

　　　　　　　　　　　至于怎么计算矩阵C呢？我们发现

　　　　　　　　　　　　　　

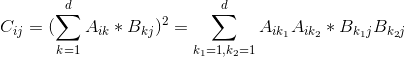
　　　　　　　　　　　所以可以将矩阵A和B分别扩展成n*(d^2)和(d^2)*n的矩阵；

　　　　　　　　　　　即将d维向量扩展成一个d^2维的向量，新向量每一维都是旧向量某两维的乘积。

　　　　　　　　　　　有了这些，步骤基本就和k=2时的情况一样了。

　　　　　　　　　　　时间复杂度：O(nd^2)

　　　　　　你会发现一个细节，数据中有n=10000,d=100,k=3的情况，n*(d^2)的空间完全不够开。

　　　　　　当然没有叫你真的开一个n*(d^2)的矩阵啊（坏笑）！你会发现涉及到矩阵乘法的操作只有在计算C*T的时候，也就是说只有4次，只要把k=3的那两次特殊抠出来处理即可，具体实现可以看小C的代码。

#include <cstdio>
#include <algorithm>
#include <cstdlib>
#define MN 100005
#define MM 105
using namespace std;
struct matrix{int **ar; int h,l;}a,b,r,h;
int g[MN],f[MM],mod,n,m,sum;

inline int read()
{
    int n=,f=;char c=getchar();
    while (c<'' || c>'') {if(c=='-')f=-; c=getchar();}
    while (c>='' && c<='') {n=n*+c-''; c=getchar();}
    return n*f;
}

matrix newmatr(int n,int m)
{
    matrix a;
    a.h=n; a.l=m;
    a.ar=new int*[n];
    for (register int i=;i<n;++i) a.ar[i]=new int[m];
    return a;
}

matrix operator*(const matrix& a,const matrix& b)
{
    matrix c=newmatr(a.h,b.l);
    register int i,j,k;
    for (i=;i<c.h;++i)
        for (j=;j<c.l;c.ar[i][j++]%=mod)
            for (c.ar[i][j]=,k=;k<a.l;++k) c.ar[i][j]+=a.ar[i][k]*b.ar[k][j];
    return c;
}

matrix operator&(const matrix& a,const matrix& b)
{
    matrix c=newmatr(a.h,b.l);
    register int i,j,kl,kr;
    for (i=;i<c.h;++i)
        for (j=;j<c.l;c.ar[i][j++]%=mod)
            for (c.ar[i][j]=,kl=;kl<a.l;++kl)
                for (kr=;kr<a.l;++kr) c.ar[i][j]+=a.ar[i][kl]*a.ar[i][kr]*b.ar[kl*a.l+kr][j];
    return c;
}

matrix operator|(const matrix& a,const matrix& b)
{
    matrix c=newmatr(a.h*a.h,b.l);
    register int i,j,k;
    for (i=;i<c.h;++i)
    {
        register int x=i/a.h,y=i%a.h;
        for (j=;j<c.l;c.ar[i][j++]%=mod)
            for (c.ar[i][j]=,k=;k<a.l;++k) c.ar[i][j]+=a.ar[x][k]*a.ar[y][k]*b.ar[k][j];
    }
    return c;
}

matrix ranmat(int n,int m)
{
    matrix a=newmatr(n,m);
    register int i,j;
    for (i=;i<n;++i)
        for (j=;j<m;++j) a.ar[i][j]=rand()%mod;
    return a;
}

int main()
{
    srand();
    register int i,j,k,o;
    n=read(); m=read(); mod=read();
    a=newmatr(n,m); b=newmatr(m,n);
    for (i=;i<n;++i)
        for (j=;j<m;++j) a.ar[i][j]=b.ar[j][i]=read()%mod;
    for (i=;i<n;g[i++]%=mod)
        for (j=;j<m;++j) g[i]+=a.ar[i][j]*a.ar[i][j];
    if (mod==)
    {
        for (o=;o<=;++o)
        {
            r=ranmat(n,);
            h=a*(b*r);
            for (i=sum=;i<n;++i) sum^=r.ar[i][];
            for (i=;i<n;++i) if (h.ar[i][]!=(sum^(r.ar[i][]&&!g[i]))) break;
            if (i<n) break;
        }
    }
    else if (mod==)
    {
        for (i=;i<n;++i) g[i]=g[i]*g[i]%mod;
        for (o=;o<=;++o)
        {
            r=ranmat(n,);
            h=a&(b|r);
            for (i=sum=;i<n;++i) sum+=r.ar[i][];
            for (i=;i<n;++i) if (h.ar[i][]!=(sum-(-g[i])*r.ar[i][])%mod) break;
            if (i<n) break;
        }
    }
    if (o>) return *printf("-1 -1");
    for (j=;j<n;++j)
    {
        if (i==j) continue;
        for (sum=k=;k<m;++k) sum+=a.ar[i][k]*a.ar[j][k];
        if (!(sum%mod)) return *printf("%d %d",min(i+,j+),max(i+,j+));
    }
}

Last Word

　　反正依着小C这属性（才不是抖M），能让他发博客吐槽的题目大概又是什么虐了他千百遍的丧题吧。（其实是因为小C智障老是打挂题）

　　一开始非常智障地跑去建n*(d^2)的矩阵，然后，然后就有了以上一段画风崩坏的代码……

　　由于用了结构体矩阵来计算，代码似乎跑得出奇地慢，洛谷和BZOJ上都过了，自家的OJ（未开O2）死活过不去……

　　所以不建议读者按矩阵计算，直接开数组即可，还有n*1的矩阵只要开成一维矩阵即可，这样代码效率可以有巨大的提升。

　　小C的代码效率较慢的锅都是因为开了二维数组，似乎 new 和 return结构体 在这道题效率还行？

　　总之，小C觉得这还算是一道挺有想法的题啦。其主要思想就是利用矩阵乘法的结合律来改变计算顺序以降低时间复杂度，还有就是在判断两个矩阵是否相等时用了一些小技巧，至于2^2≡1(mod 3)什么的就是脑洞问题了吧！（QAQ觉得脑洞平了）