[Bayes] Why we prefer Gaussian Distribution
最后还是选取一个朴素直接的名字,在此通过手算体会高斯的便捷和神奇。
Ref: The Matrix Cookbook
注意,这里的所有变量默认都为多元变量,不是向量就是矩阵。多元高斯密度函数如下:

高斯的线性组合结果y还是高斯
期望答案很直接。

方差需要计算,注意其中的矩阵计算技巧,要记下来。

高斯相乘还是高斯

如下计算用到了8.1.8。这里的tricky是:8.1.8之后得到的结果虽然复杂,但
我们想尽办法做出z的分布,就是为了在之后的积分中直接干掉z,也便留下了我们需要的p(x)。
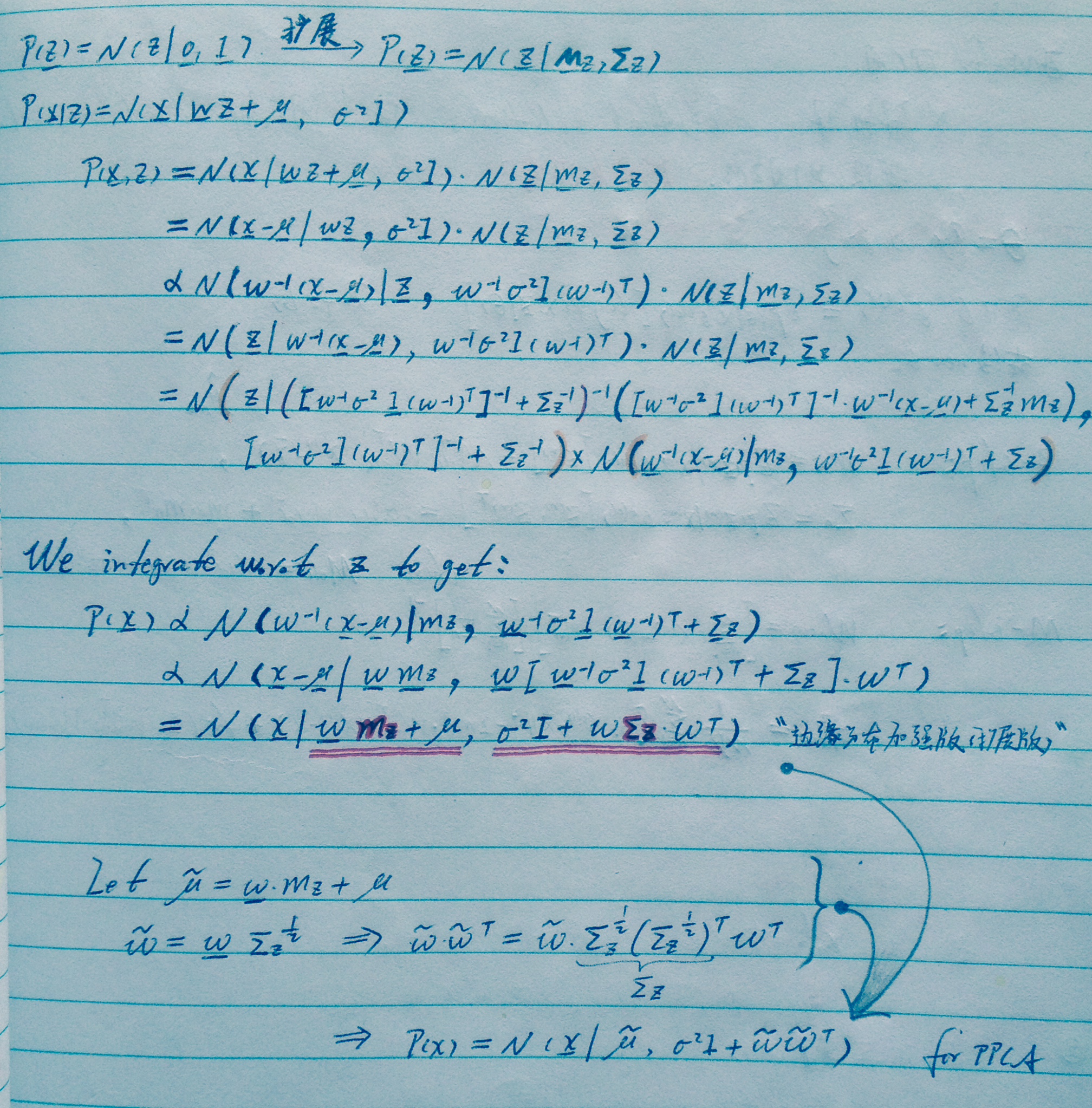
[Bayes] Why we prefer Gaussian Distribution的更多相关文章
- 一起啃PRML - 1.2.4 The Gaussian distribution 高斯分布 正态分布
一起啃PRML - 1.2.4 The Gaussian distribution 高斯分布 正态分布 @copyright 转载请注明出处 http://www.cnblogs.com/chxer/ ...
- 正态分布(Normal distribution)又名高斯分布(Gaussian distribution)
正态分布(Normal distribution)又名高斯分布(Gaussian distribution),是一个在数学.物理及project等领域都很重要的概率分布,在统计学的很多方面有着重大的影 ...
- UNDERSTANDING THE GAUSSIAN DISTRIBUTION
UNDERSTANDING THE GAUSSIAN DISTRIBUTION Randomness is so present in our reality that we are used to ...
- 高斯分布(Gaussian Distribution)的概率密度函数(probability density function)
高斯分布(Gaussian Distribution)的概率密度函数(probability density function) 对应于numpy中: numpy.random.normal(loc= ...
- 广义逆高斯分布(Generalized Inverse Gaussian Distribution)及修正贝塞尔函数
1. PDF generalized inverse Gaussian distribution (GIG) 是一个三参数的连续型概率分布: f(x)=(a/b)p/22Kp(ab−−√)xp−1e− ...
- 【翻译】拟合与高斯分布 [Curve fitting and the Gaussian distribution]
参考与前言 英文原版 Original English Version:https://fabiandablander.com/r/Curve-Fitting-Gaussian.html 如何通俗易懂 ...
- 吴恩达机器学习笔记56-多元高斯分布及其在误差检测中的应用(Multivariate Gaussian Distribution & Anomaly Detection using the Multivariate Gaussian Distribution)
一.多元高斯分布简介 假使我们有两个相关的特征,而且这两个特征的值域范围比较宽,这种情况下,一般的高斯分布模型可能不能很好地识别异常数据.其原因在于,一般的高斯分布模型尝试的是去同时抓住两个特征的偏差 ...
- 吴恩达机器学习笔记53-高斯分布的算法(Algorithm of Gaussian Distribution)
如何应用高斯分布开发异常检测算法呢? 异常检测算法: 对于给定的数据集
- 吴恩达机器学习笔记52-异常检测的问题动机与高斯分布(Problem Motivation of Anomaly Detection& Gaussian Distribution)
一.问题动机 异常检测(Anomaly detection)问题是机器学习算法的一个常见应用.这种算法的一个有趣之处在于:它虽然主要用于非监督学习问题,但从某些角度看,它又类似于一些监督学习问题. 给 ...
随机推荐
- MySQL之多表操作
前言:之前已经针对数据库的单表查询进行了详细的介绍:MySQL之增删改查,然而实际开发中业务逻辑较为复杂,需要对多张表进行操作,现在对多表操作进行介绍. 前提:为方便后面的操作,我们首先创建一个数据库 ...
- .net窗体程序的基础知识及详细笔记
第一章:初识Windows程序 1.1:第一个wondows程序 1.1.1:认识windows程序 Form1.cs:窗体文件:程序对窗体编写的代码一般都存放在这个文件(还有拖动控件时的操作和布局, ...
- 30分钟快速学习Shell脚本编程
什么是Shell脚本 示例 看个例子吧: #!/bin/sh cd ~ mkdir shell_tut cd shell_tut for ((i=0; i<10; i++)); do touch ...
- JS - Function 之 Arguments
Arguments 函数的参数构成的数组 描述 只定义在函数体内,函数体内arugments指代Arguments对象,该对象是类数组对象,有数组属性可以当做数组使用,含有传入该函数的所有参数,aru ...
- WebApi实现验证授权Token,WebApi生成文档等
using System; using System.Linq; using System.Web; using System.Web.Http; using System.Web.Security; ...
- 数据库表反向生成(二) Django ORM inspectdb
在前一篇我们说了,mybatis-generator反向生成代码. 这里我们开始说如何在django中反向生成mysql model代码. 我们在展示django ORM反向生成之前,我们先说一下怎么 ...
- hs_err_pid
hs_err_pid这种文件,是JVM出现错误时dump下来的.记录了错误发生当时: 1)JVM的状态参数 2)Linux的状态参数 就以下面的文件为例: # # There is insuffici ...
- JVM性能调优,GC
刚刚做完了一个项目的性能测试,“有幸”也遇到了内存泄露的案例,所以在此和大家分享一下. 主要从以下几部分来说明,关于内存和内存泄露.溢出的概念,区分内存泄露和内存溢出:内存的区域划分,了解GC回收机制 ...
- 上传代码 CodePlex
博客园作为博客备份,博客会更新一份在博客园 CodePlex是微软开源项目网站,有很多人都在上面传代码,我们也可以上传自己的代码 注册 我们可以用微软账号注册,填写用户名.密码,很快就好. 新建项目 ...
- crontab的使用方法
cron是一个linux下的定时执行工具,可以在无需人工干预的情况下运行作业. /sbin/service crond start //启动服务 /sbin/service crond stop // ...
