玛雅游戏[NOIP2011]

题目描述

Mayan puzzle 是最近流行起来的一个游戏。游戏界面是一个7 行5 列的棋盘，上面堆放着一些方块，方块不能悬空堆放，即方块必须放在最下面一行，或者放在其他方块之上。游戏通关是指在规定的步数内消除所有的方块，消除方块的规则如下：

1、 每步移动可以且仅可以沿横向（即向左或向右）拖动某一方块一格：当拖动这一方块时，如果拖动后到达的位置（以下称目标位置）也有方块，那么这两个方块将交换位置（参见输入输出样例说明中的图6 到图7）；如果目标位置上没有方块，那么被拖动的方块将从原来的竖列中抽出，并从目标位置上掉落（直到不悬空，参见下面图1 和图2）；

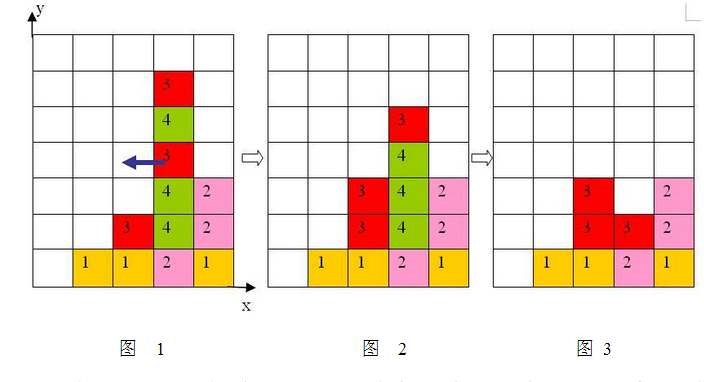
2、 任一时刻，如果在一横行或者竖列上有连续三个或者三个以上相同颜色的方块，则它们将立即被消除（参见图1 到图3）。

注意：
a) 如果同时有多组方块满足消除条件，几组方块会同时被消除（例如下面图4，三个颜色为1 的方块和三个颜色为2 的方块会同时被消除，最后剩下一个颜色为2 的方块）。
b) 当出现行和列都满足消除条件且行列共享某个方块时，行和列上满足消除条件的所有方块会被同时消除（例如下面图5 所示的情形，5 个方块会同时被消除）。

3、 方块消除之后，消除位置之上的方块将掉落，掉落后可能会引起新的方块消除。注意：掉落的过程中将不会有方块的消除。

上面图1 到图3 给出了在棋盘上移动一块方块之后棋盘的变化。棋盘的左下角方块的坐标为（0, 0），将位于（3, 3）的方块向左移动之后，游戏界面从图1 变成图2 所示的状态，此时在一竖列上有连续三块颜色为4 的方块，满足消除条件，消除连续3 块颜色为4 的方块后，上方的颜色为3 的方块掉落，形成图3 所示的局面。

输入

输入文件mayan.in，共6 行。
第一行为一个正整数n，表示要求游戏通关的步数。
接下来的5 行，描述7*5 的游戏界面。每行若干个整数，每两个整数之间用一个空格隔开，每行以一个0 结束，自下向上表示每竖列方块的颜色编号（颜色不多于10 种，从1 开始顺序编号，相同数字表示相同颜色）。
输入数据保证初始棋盘中没有可以消除的方块。

 

输出

如果有解决方案，输出n 行，每行包含3 个整数x，y，g，表示一次移动，每两个整数之间用一个空格隔开，其中（x，y）表示要移动的方块的坐标，g 表示移动的方向，1 表示向右移动，-1 表示向左移动。注意：多组解时，按照x 为第一关健字，y 为第二关健字，1优先于-1，给出一组字典序最小的解。游戏界面左下角的坐标为（0，0）。
如果没有解决方案，输出一行，包含一个整数-1。

 

样例输入

3
1 0
2 1 0
2 3 4 0
3 1 0
2 4 3 4 0

样例输出

2 1 1
3 1 1
3 0 1

提示

按箭头方向的顺序分别为图6 到图11

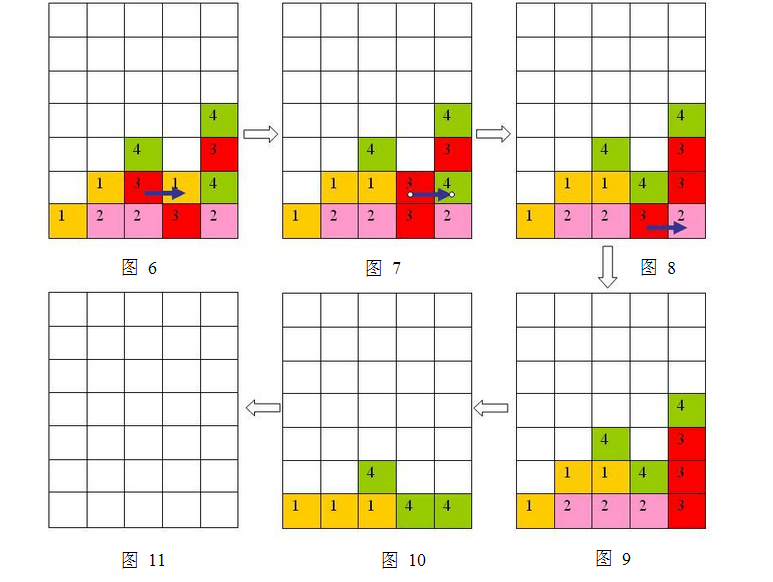
样例输入的游戏局面如上面第一个图片所示，依次移动的三步是：（2，1）处的方格向右移动，（3，1）处的方格向右移动，（3，0）处的方格向右移动，最后可以将棋盘上所有方块消除。

【数据范围】

对于30%的数据，初始棋盘上的方块都在棋盘的最下面一行；

对于100%的数据，0 < n≤5。

【题解】

     昨天考试简直迷之做题状态啊。读完题，打了两个暴力，毫无预兆地开始肚子疼，几乎坐不住，趴了多半个上午,后来头晕，莫名还很困。还是不想弃疗，然后在演草纸上写来写去，也没打出什么名堂。然后挨到十二点多，非常万念俱灰地交了卷回宿舍躺着。一整天都难受。

玛雅游戏这题明显是个搜索了，但是一开始打算广搜。看图以为是俄罗斯方块，看题发现是开心消消乐= =，要模拟这么个游戏程序还真不容易。想了想像移动玩具那样，拿哈希什么的水一水，但是这道题并没有什么标准状态，存一下全空好像也没什么意义。好像过了很久才发现好像给出了步数，而且应该还是一定的，题目这是整个读错了呀这个。然后发现，好像有步数我也不会搜？终于彻底弃疗，迷失在传参中无法自拔。想象中这样一个程序应该是分区分功能明显，而且非常简洁的。

最后改过的代码，确实是各个部分功能清晰的。特别让我没想到的，是每次dfs之前复制矩阵，便于回溯。消除函数wipe，用bool型标记了全部可消去块之后一起消除，只要有消除块就要重新调用fall函数。下落函数fall，把所有空块下落之后再调用wipe函数。移动函数move，记录每次的移动操作并开始调用fall。深搜函数dfs，直接按规定的字典序从小到大枚举移动块调用move，每次dfs后还原矩阵。只要在dfs里搜到了一个可行解就直接exit(0)结束整个程序，第一个搜到的解就是最优解，最后都没搜到解就是无解了。

值得一提的是，考试时非常让我头疼的传参在这份代码里降到了最少，很麻烦的记录方案也因为dfs只记录当前解变得非常简单。改题的时候fall函数错过，还原矩阵不够及时，减少了枚举左移次数(左边有块的，左移当前块一定不如把左边的块右移优)和相同块次数(交换相同的好像没什么意义)解决了超时问题，最后居然因为从读入开始的边界问题卡了一个多小时(社会生产效率及其低下！)，折腾到将近下晚三才改完。大搜索的第二题，感觉很有成就感，也很有意思。希望以后多调几道这样的题，如果比赛遇到搜索题也能有入手点。

#include<iostream>
#include<cstdio>
#include<cstdlib>
#include<cstring>
using namespace std;
int n,a[][],temp;
bool xq[][];
void init()
{
     scanf("%d",&n);
     for(int i=;i<;i++)
       for(int j=;j<;j++)
       {
          scanf("%d",&a[i][j]);
          if(a[i][j]==) break;
       }
}
void wipe();
void fall()
{
     for(int i=;i<;i++)
       for(int j=;j<;j++)
       {
          temp=j-;
          while(temp>=&&!a[i][temp]&&a[i][temp+])
          {
            a[i][temp]=a[i][temp+];
            a[i][temp+]=;
            temp--;
          }
       }
     wipe();
}
bool bd,qk;
void wipe()
{
     for(int i=;i<;i++)
       for(int j=;j<;j++)
         if(a[i][j])
         {
           if(i!=&&i!=)
             if(a[i-][j]==a[i][j]&&a[i][j]==a[i+][j])
               xq[i-][j]=xq[i][j]=xq[i+][j]=;
           if(j!=&&j!=)
             if(a[i][j-]==a[i][j]&&a[i][j]==a[i][j+])
               xq[i][j-]=xq[i][j]=xq[i][j+]=;
         }
     bd=;
     for(int i=;i<;i++)
       for(int j=;j<;j++)
         if(xq[i][j])
           a[i][j]=,xq[i][j]=,bd=;
     if(bd) fall();
}
int ax[],ay[],ad[];
void move(int x,int y,int fx,int bs)
{
     if(fx==)
     {
        temp=a[x+][y];
        a[x+][y]=a[x][y];
        a[x][y]=temp;
        ax[bs]=x;
        ay[bs]=y;
        ad[bs]=fx;
        fall();
     }
     if(fx==-)
     {
        temp=a[x-][y];
        a[x-][y]=a[x][y];
        a[x][y]=temp;
        ax[bs]=x;
        ay[bs]=y;
        ad[bs]=fx;
        fall();
     }
}
void dfs(int z)
{
     if(z>n) return;
     if(z==n)
     {
       qk=;
       for(int i=;i<;i++)
         for(int j=;j<;j++)
           if(a[i][j]) qk=;
       if(qk)
       {
         for(int i=;i<=n;i++)
           printf("%d %d %d\n",ax[i],ay[i],ad[i]);
         exit();
       }
       return;
     }
     int ww[][];
     memcpy(ww,a,sizeof(a));
     for(int i=;i<;i++)
       for(int j=;j<;j++)
       {
          if(!a[i][j])  break;
          if(i!=&&a[i+][j]!=a[i][j])
          {
             move(i,j,,z+);
             dfs(z+);
             memcpy(a,ww,sizeof(ww));
          }
          if(i!=&&!a[i-][j])
          {
             move(i,j,-,z+);
             dfs(z+);
             memcpy(a,ww,sizeof(ww));
          }
       }
}
int main()
{
    freopen("mayan.in","r",stdin);
    freopen("mayan.out","w",stdout);
    init();
    dfs();
    printf("-1");
    return ;
}