10.04 FZSZ模拟Day1 总结

今天轮到FZSZ出题了，这可是连续两年捧杯NOI的学校了……

可想而知今天题难度有多大……不过似乎还要庆幸出题的是一位叫Anzhe Wang 的大神而不是fjzzq？

T1.permutation

期望得分40，实际得分40.

这道题看起来很像是组合题……想起昨天的组合题，想试试能不能用类似的做法去做。后来发现不可行，不可递推，因为昨天的题其实还很良心，只是相邻两个元素之间会互相影响，而这个题前面的元素会影响到后面的元素，所以难以递推。

我大概开场想了30min没思路 然后就去看后面了……

回来大概一想想到这题40pts可以用状压DP水过，就是某一位上是i表示那一位当前是被选取状态，这样其实我们是可以通过转移来确定先后顺序的。这样复杂度是O（2^n * n）的，可以过40pts。

然后看了题解……题解真是让人脑洞大开……其实我们发现这个选取的情况可以对应一个二分图。我们把所有的pi放在一个点集，所有的i（也可以理解为位置）放在一个点集。

如果我们令二分图中的连边表示实际匹配时的不合法情况，我们会得到以下的图。

 

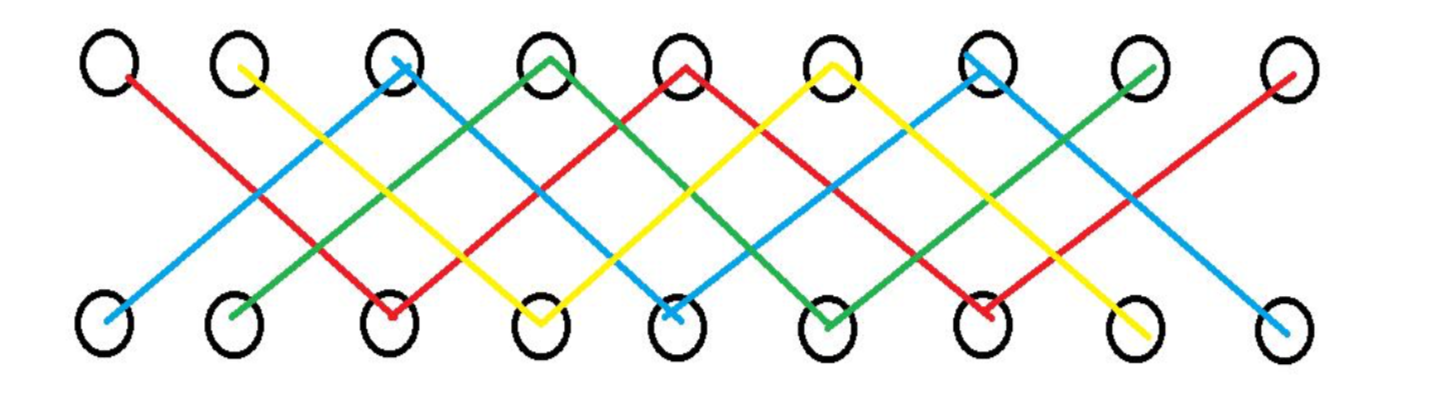
也就是说，这个二分图是由许多条不相交的链组成的（所谓的不相交是指没有属于不同链的两条边连在一个点上），那么我们要求的其实就是这个二分图的补图的匹配方案数。（补图简单的定义就是，原二分图中有的边它没有，原来没有的边他有。）

我们令g[i]表示在这个二分图中选取i条边的方案数（也就是等于确定了i个不合法的情况）

那么我们得到答案有如下式子：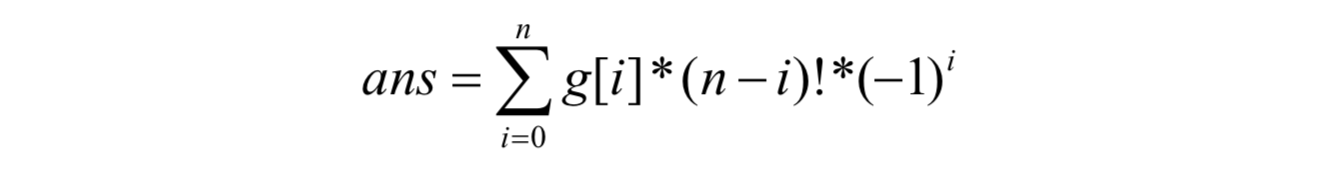

来解释一下，首先（n-i）!表示一个全排列，就是因为你当前确定有i条边是不合法的，那么剩余的n-i条边就是自由排列的，那就是它的阶乘次的方案数。后面的是什么意思呢？首先我们知道如果啥都不管的话，那么n！是所有的情况，但是你在n！种的情况之中，必然会统计到有一条边是不合法的情况，于是乎我们就要去计算有一条边不合法的情况，然后把它减掉。但是在这样计算的时候又会多把有两条边不合法的情况减掉，相当于多减了，然后我们还得给加回来……所以这样层层递推就有了最后的式子。

然后我们去求g[i]，用f[i][j][0/1]表示在一条链上取到第i个点，取了j条链，当前点取或者没取的情况数，那么就有转移：

f[i][j][0] = f[i-1][j][1] + f[i-1][j][0];

f[i][j][1] = f[i-1][j-1][0];

最后我们直接用f把g合并出来就可以了。时间复杂度是O（n^2/k + n）？能过95.最后一个点什么NTT真的不会……

然而这个也不想写……

40pts状压代码：

#include<iostream>
#include<cstdio>
#include<cmath>
#include<algorithm>
#include<queue>
#include<cstring>
#include<utility>
#include<map>
#define pr pair<int,int>
#define mp make_pair
#define fi first
#define sc second
#define lowbit(x) x & (-x)
#define rep(i,a,n) for(int i = a;i <= n;i++)
#define per(i,n,a) for(int i = n;i >= a;i--)
#define enter putchar('\n')
using namespace std;
typedef long long ll;
const int M = ;
const int N = ;
const ll mod = ;

int read()
{
    int ans = ,op = ;
    char ch = getchar();
    while(ch < '' || ch > '')
    {
        if(ch == '-') op = -;
        ch = getchar();
    }
    while(ch >='' && ch <= '')
    {
        ans *= ;
        ans += ch - '';
        ch = getchar();
    }
    return ans * op;
}

int n,k,cur;
ll dp[M];

int getsum(int x)
{
    int s = ;
    while(x) s++,x -= lowbit(x);
    return s;
}

int main()
{
    freopen("permutation.in","r",stdin);
    freopen("permutation.out","w",stdout);
    n = read(),k = read();
    rep(i,,n-) if(i != k) dp[<<i] = ;
    rep(i,,(<<n)-)
    {
        int h = getsum(i);
        rep(j,,n-)
        {
            if(i & ( << j) || (abs(j-h) == k)) continue;
            dp[i | ( << j)] += dp[i],dp[i | ( << j)] %= mod;
        }
    }
    printf("%lld\n",dp[(<<n)-]);
    return ;
}

看一下学姐的代码。

#include <iostream>
#include <cstdio>
#include <cstring>
#include <algorithm>
#include <ctime>
#define fi first
#define se second
#define pii pair<int,int>
#define mp make_pair
#define enter putchar('\n')
#define space putchar(' ')
//#define ivorysi
#define MAXN 100005
typedef long long int64;
using namespace std;
template<class T>
void read(T &res) {
    res = ;char c = getchar();T f = ;
    while(c < '' || c > '') {
        if(c == '-') f = -;
        c = getchar();
    }
    while(c >= '' && c <= '') {
        res = res *  + c - '';
        c = getchar();
    }
    res *= f;
}
template<class T>
void out(T x) {
    if(x < ) {x = -x;putchar('-');}
    if(x >= ) {
        out(x / );
    }
    putchar('' + x % );
}
const int MOD = ;
int inc(int a,int b) {
    return a + b >= MOD ? a + b - MOD : a + b;
}
int mul(int a,int b) {
    return 1LL * a * b % MOD;
}
void update(int &x,int y) {
    x = inc(x,y);
}
int fac[MAXN],N,K,g[MAXN],f[ * ][][];
bool vis[][MAXN];
void DP(int st,int cnt) {
    for(int j =  ; j <= N ; ++j) update(f[st + ][j][],inc(f[st][j][],f[st][j][]));
    for(int h = st +  ; h <= st + cnt ; ++h) {
        for(int j =  ; j <= N ; ++j) {
            update(f[h][j][],inc(f[h - ][j][],f[h - ][j][]));
            if(j >= ) update(f[h][j][],f[h - ][j - ][]);
        }
    }
}
void Solve() {
    read(N);read(K);
    fac[] = ;
    for(int i =  ; i <= N ; ++i) fac[i] = mul(fac[i - ],i);
    int tot = ;
    memset(vis,,sizeof(vis));
    f[][][] = ;
    for(int i =  ; i <= N ; ++i) {
        if(!vis[][i]) {
            int cnt = ;
            for(int j = i ; j <= N ; j +=  * K) {
                vis[][j] = ;
                cnt++;
                if(j + K <= N) {vis[][j + K] = ;++cnt;}
            }
            DP(tot,cnt);
            tot += cnt;
        }
        if(!vis[][i]) {
            int cnt = ;
            for(int j = i ; j <= N ; j +=  * K) {
                vis[][j] = ;
                ++cnt;
                if(j + K <= N) {
                    vis[][j + K] = ;++cnt;
                }
            }
            DP(tot,cnt);
            tot += cnt;
        }
    }
    for(int i =  ; i <= N ; ++i) {
        g[i] = inc(f[ * N][i][],f[ * N][i][]);
    }
    int t = ,ans = ;
    for(int i =  ; i <= N ; ++i) {
        update(ans,mul(t,mul(g[i],fac[N - i])));
        t = mul(t,MOD - );
    }
    out(ans);enter;
}
int main() {
#ifdef ivorysi
    freopen("f1.in","r",stdin);
#else
    freopen("permutation.in","r",stdin);
    freopen("permutation.out","w",stdout);
#endif
    Solve();
    return ;
}

T2.tree

期望得分30，实际得分40

这题大概看了20多分钟，没什么思路，但是可以疯狂爆搜，暴力枚举哪两条边要删除，然后暴力dfs判断图是否联通，复杂度O（n^3）,得分40.

这道题的60pts做法是枚举每一条原来的树边，之后对新图跑他让tarjan去求桥，每座非树边的桥有1的贡献。

然后满分的做法就是，我们发现对于一条树边，一棵子树内的所有节点如果有两条或者以上连了出去，那么你怎么割也无法割断，如果只有一条，那么就有1的贡献，如果没有，那就随便找一条割断，也就是有m的贡献。

所以我们可以进行树上差分。对于每一条新加的边，我们把它拆成从一个点到LCA和另一个点到LCA的两条路径，分别差分维护。最后我们统计一下，每个点的点权为1则有1的贡献，为0有m的贡献。

我写的时候是用树剖的，也能过300000.

然后学姐还有更强的操作，直接维护dfs序，统计一个子树管辖的区间之内能向左/右延伸的最远的两条边能延伸到的范围，最后统计的时候如果有两天或以上的边，你就割不断，有一条贡献为1，0条则贡献为m。（%学姐orz）

40pts爆搜不看了，直接上100的树剖。

#include<iostream>
#include<cstdio>
#include<cmath>
#include<algorithm>
#include<queue>
#include<cstring>
#include<utility>
#include<map>
#define pr pair<int,int>
#define mp make_pair
#define fi first
#define sc second
#define rep(i,a,n) for(int i = a;i <= n;i++)
#define per(i,n,a) for(int i = n;i >= a;i--)
#define enter putchar('\n')
using namespace std;
typedef long long ll;
const int M = ;
const int N = ;

int read()
{
    int ans = ,op = ;
    char ch = getchar();
    while(ch < '' || ch > '')
    {
        if(ch == '-') op = -;
        ch = getchar();
    }
    while(ch >= '' && ch <= '')
    {
        ans *= ;
        ans += ch - '';
        ch = getchar();
    }
    return ans * op;
}

struct edge
{
    int next,to;
}e[M<<];

struct seg
{
    int v,lazy;
}t[M<<];

int n,m,dfn[M],head[M],ecnt,size[M],fa[M],dep[M],top[M],hson[M],idx,ch[M],x,y;
ll ans;

void add(int x,int y)
{
    e[++ecnt].to = y;
    e[ecnt].next = head[x];
    head[x] = ecnt;
}

void dfs1(int x,int f,int depth)
{
    fa[x] = f,dep[x] = depth,size[x] = ;
    int maxson = -;
    for(int i = head[x];i;i = e[i].next)
    {
        if(e[i].to == f) continue;
        dfs1(e[i].to,x,depth+);
        size[x] += size[e[i].to];
        if(size[e[i].to] > maxson) maxson = size[e[i].to],hson[x] = e[i].to;
    }
}

void dfs2(int x,int t)
{
    top[x] = t,dfn[x] = ++idx;
    if(!hson[x]) return;
    dfs2(hson[x],t);
    for(int i = head[x];i;i = e[i].next)
    {
        if(e[i].to == fa[x] || e[i].to == hson[x]) continue;
        dfs2(e[i].to,e[i].to);
    }
}

void pushdown(int p,int l,int r)
{
    int mid = (l+r) >> ;
    t[p<<].lazy += t[p].lazy,t[p<<|].lazy += t[p].lazy;
    t[p<<].v += t[p].lazy * (mid-l+),t[p<<|].v += t[p].lazy * (r-mid);
    t[p].lazy = ;
}

void modify(int p,int l,int r,int kl,int kr)
{
    if(l == kl && r == kr)
    {
        t[p].v += (r-l+),t[p].lazy++;
        return;
    }
    int mid = (l+r) >> ;
    if(t[p].lazy) pushdown(p,l,r);
    if(kr <= mid) modify(p<<,l,mid,kl,kr);
    else if(kl > mid) modify(p<<|,mid+,r,kl,kr);
    else modify(p<<,l,mid,kl,mid),modify(p<<|,mid+,r,mid+,kr);
}

int query(int p,int l,int r,int pos)
{
    if(l == r) return t[p].v;
    int mid = (l+r) >> ;
    if(t[p].lazy) pushdown(p,l,r);
    if(pos <= mid) return query(p<<,l,mid,pos);
    else return query(p<<|,mid+,r,pos);
}

void mrange(int x,int y)
{
    while(top[x] != top[y])
    {
        if(dep[top[x]] < dep[top[y]]) swap(x,y);
        modify(,,n,dfn[top[x]],dfn[x]);
        x = fa[top[x]];
    }
    if(dep[x] > dep[y]) swap(x,y);
    if(dfn[x] +  > dfn[y]) return;
    modify(,,n,dfn[x]+,dfn[y]);
}

int main()
{
//    freopen("tree.in","r",stdin);
//    freopen("tree.out","w",stdout);
    n = read(),m = read();
    rep(i,,n-) x = read(),y = read(),add(x,y),add(y,x);
    dfs1(,,),dfs2(,);
    rep(i,,m) x = read(),y = read(),mrange(x,y);
    rep(i,,n) ans += (query(,,n,dfn[i]) == );
    rep(i,,n) ans += (query(,,n,dfn[i]) == ) * m;
    printf("%lld\n",ans);
    return ;
}

T3.polynomial

期望得分30，实际得分0.

这道题是真心不可做……题解里面什么FFT是搞哪样……

考试的时候暴力打表n<=4的情况，结果发现自己推4个一样的时候推错了，多推了3个，爆零。

还是放上改好的暴力打表30吧……正解代码11kb又是哪样……

#include<iostream>
#include<cstdio>
#include<cmath>
#include<algorithm>
#include<queue>
#include<cstring>
#include<utility>
#include<map>
#define pr pair<int,int>
#define mp make_pair
#define fi first
#define sc second
#define rep(i,a,n) for(int i = a;i <= n;i++)
#define per(i,n,a) for(int i = n;i >= a;i--)
#define enter putchar('\n')
using namespace std;
typedef long long ll;
const int M = ;
const int N = ;

int read()
{
    int ans = ,op = ;
    char ch = getchar();
    while(ch < '' || ch > '')
    {
        if(ch == '-') op = -;
        ch = getchar();
    }
    while(ch >='' && ch <= '')
    {
        ans *= ;
        ans += ch - '';
        ch = getchar();
    }
    return ans * op;
}

struct card
{
    int num,col;
}c[];

int T,n,posa,posb,cur;
char s[];
bool jok;

void clear()
{
    memset(c,,sizeof(c));
    jok = ,cur = posa = posb = ;
}

bool same()
{
    return (c[].num == c[].num) && (c[].num == c[].num) && (c[].num == c[].num);
}

bool ssame()
{
    rep(i,,n)
    {
        rep(j,i+,n)
        rep(k,j+,n)
        if((c[i].num == c[j].num) && (c[j].num == c[k].num)) return ;
    }
    return ;
}

bool tsame()
{
    rep(i,,n)
    {
        rep(j,i+,n)
        if(c[i].num == c[j].num)
        {
            posa = i,posb = j;
            return ;
        }
    }
    return ;
}

void naive()
{
    if(n == )
    {
        printf("1\n");
        return;
    }
    if(n == )
    {
        if(c[].num == c[].num) printf("2\n");
        else if(c[].num + c[].num == ) printf("2\n");
        else printf("1\n");
        return;
    }
    if(n == )
    {
        if(c[].num == c[].num && c[].num == c[].num) printf("5\n");
        else
        {
            rep(i,,n)
            rep(j,i+,n)
            {
                if(c[i].num == c[j].num || c[i].num + c[j].num == )
                {
                    printf("2\n");
                    return;
                }
            }
            printf("1\n");
            return;
        }
    }
    rep(i,,n)
    {
        rep(j,i+,n)
        if(c[i].num + c[j].num == ) jok = ;
    }
    if(jok)
    {
        rep(i,,n)
        rep(j,i+,n)
        {
            if(c[i].num == c[j].num)
            {
                printf("4\n");
                return;
            }
        }
        printf("2\n");
        return;
    }
    if(same())
    {
        printf("15\n");
        return;
    }
    if(ssame())
    {
        printf("6\n");
        return ;
    }
    if(tsame())
    {
        cur = ;
        rep(i,,n)
        {
            if(i == posa || i == posb) continue;
            if(cur == c[i].num)
            {
                printf("4\n");
                return;
            }
            if(!cur) cur = c[i].num;
        }
        printf("2\n");
        return;
    }
    printf("1\n");
    return;
}

int main()
{
    freopen("polynomial.in","r",stdin);
    freopen("polynomial.out","w",stdout);
    srand();
    T = read();
    while(T--)
    {
        clear();
        n = read();
        rep(i,,n)
        {
            scanf("%s",s);
            if(s[] >= '' && s[] <= '') c[i].num = s[] - '';
            else if(s[] < '' || s[] > '') c[i].num = s[] - 'A' + ;
            else c[i].num =  + s[] - '';
        }
        rep(i,,n) c[i].col = read();
        if(n <= ) naive();
        else printf("%d\n",rand());
    }
    return ;
}

感觉自己还是太弱，不知道明天能咋样orz。