CF578D. LCS Again

n<=100000个字符的小写字母串，问用前m<=26个小写字母能拼出多少个和原串lcs=n-1的字符串。

首先把字符串划分成若干个连续相同的段，如aaa|bb|c|dd，然后题目即要求从里面挖掉一个再丢回去一个。如挖掉a，那么就剩aa|bb|c|dd，可以发现一个连续相同段挖谁都一样所以一个连续相同段只算一次，然后补一个。可以发现在自己的相同段中不能丢一个和原来一样的，而在其他地方同一个字母前后丢一样的会算重，如aab b bcdd，和aabb b cdd，也就是在第二个b前后丢b效果相同，所以每个地方只能放m-1个字符，就加上n*(m-1)。

然而还会算重。。比如ababab这样的连续段，任意挖一个补到后面一定对应一个后面补到前面的方案，比如这里把第一个a补到最后变成bababa，和把最后一个b提到最前是一样的。假设有一段连续的abab……串长度len，那么他有len*(len-1)/2个abab……的子串，就减掉即可。

 #include<stdio.h>
 #include<string.h>
 #include<stdlib.h>
 #include<algorithm>
 //#include<iostream>
 using namespace std;

 int n,m;
 #define maxn 200011
 char s[maxn];

 int main()
 {
     scanf("%d%d",&n,&m);
     scanf("%s",s+);
     #define LL long long
     LL ans=n*(m-);
     for (int i=;i<=n;i++) if (s[i]!=s[i-]) ans+=n*(m-);
     int len=;
     for (int i=;i<=n;i++)
     {
         if (len==) if (s[i-]!=s[i]) len++;else{}
         else if (s[i-]==s[i]) len++;
         else
         {
             ans-=1ll*len*(len-)/;
             if (s[i]==s[i-]) len=;
             else len=;
         }
     }
     ans-=1ll*len*(len-)/;
     printf("%lld\n",ans);
     return ;
 }

YYL的做法：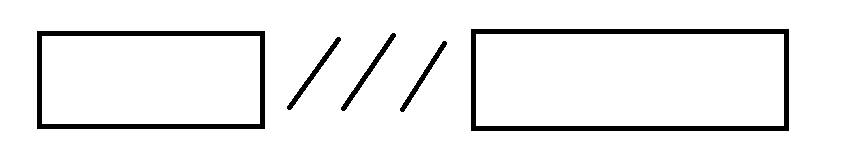

关注这种匹配方式的开始条件和结尾条件，即每个位置作为斜线区域开始的方案数，作为终止区域结束的方案数。需要分个类：

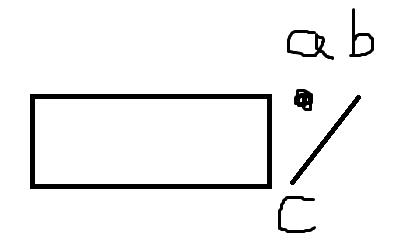
这里a!=b会有1的开始位置贡献。

这里若a=b，d会有m-1种结束方式；若a!=b，d会有m-2种结束方式。

待填坑。