HDU——1787 GCD Again

题意：

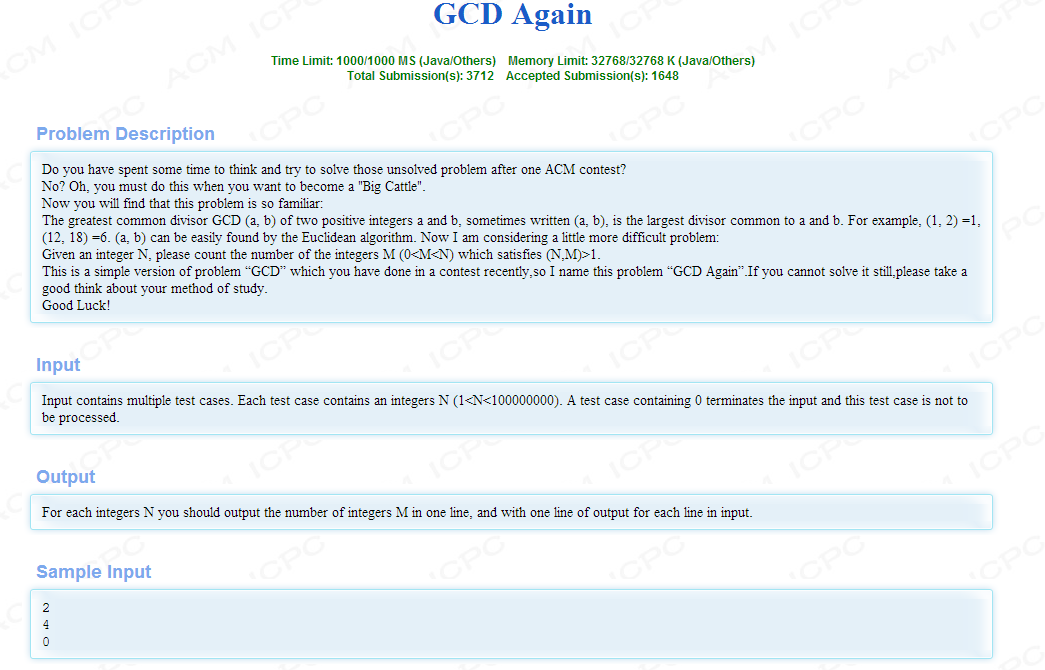
在一次acm竞赛之后，你花了一些时间去思考和尝试解决那些未解决的问题吗？
不知道？哦，当你想成为“大牛”的时候，你就必须这样做。
现在你会发现，这个问题是如此熟悉：
两个正整数a和b的最大GCD(a，b)，有时是写(a，b)，是a和b的最大除数，例如(，)=，(，)=。(a，b)可以很容易地找到欧几里德算法。现在，我正在考虑一个更难的问题：
给定一个整数n，请计算一个满足gcd(n，m)>1的整数m(0<m<n)的个数。
这是一个简单版本的问题“GCD”，你在最近的比赛中做了，所以我把这个问题命名为“GCD”。如果你还不能解决它，请好好考虑一下你的学习方法。
祝好运

思路：

我们要求gcd（n,m）大于一的m的个数，那我们只要求出来gcd（n,m）=1的个数，再用总的减去不就好了吗。。。

所以，裸题，欧拉函数

（这个题目好像有点小问题，应该不能输出负数，但好像标程输入1时输出-1.。。。）

代码：

#include<cstdio>
#include<cstring>
#include<cstdlib>
#include<iostream>
#include<algorithm>
using namespace std;
int t,n,ans;
int read()
{
    ,f=; char ch=getchar();
    ; ch=getchar();}
    +ch-'; ch=getchar();}
    return x*f;
}
int get_phi(int x)
{
    int sum=x;
    ==)
    {
        ==) x/=;
        sum/=;
    }
    ;i*i<=x;i+=)
    {
        )
        {
           ) x/=i;
           sum=sum/i*(i-);
        }
    }
    ) sum=sum/x*(x-);
    return sum;
}
int main()
{
    )
    {
        n=read();
        ) break;
        ans=n-get_phi(n)-;
        printf("%d\n",ans);
    }
    ;
}