机器学习_决策树Python代码详解

决策树优点：计算复杂度不高，输出结果易于理解，对中间值的缺失不敏感，可以处理不相关特征数据；

决策树缺点：可能会产生过度匹配问题。

决策树的一般步骤：

（1）代码中def 1，计算给定数据集的香农熵：

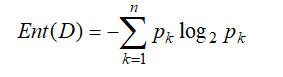
其中n为类别数，D为数据集，每行为一个样本，p_k  表示当前样本集合D中第k类样本所占的比例，Ent(D)越小，D的纯度越高，即表示D中样本大部分属于同一类；反之，D的纯度越低，即数据集D中的类别数比较多。

（2）代码中def 2，选择最好的数据集划分方式，即选择信息增益最大的属性：

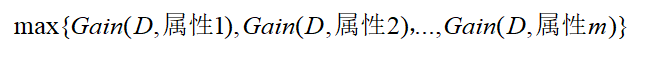
其中

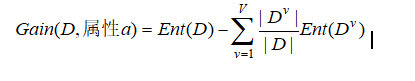
这里V表示属性a的可能的取值数，D^v表示属性a上取值为a^v的样本。

（3）代码中 def 3，按照给定特征划分数据集：选取最优属性后，再从属性的各个取值中选取最优的属性，以此类推。

（4）代码中def 5，递归构造树，数的结束标志为：a、类别完全相同则停止划分；b、代码中def 4，如果数据集已经处理了所有属性，但是类标签依然不是唯一的，此时采用多数表决法，即遍历完所有特征时返回出现次数最多的类别。

from math import log

# 计算数据集的信息熵，熵越小，说明数据集的纯度越高
def calcShannonEnt(dataset):   # def 1
    numEntries = len(dataset)   # 样本数，这里的dataSet是列表
    labelCounts = {}  #定义一个字典，key为类别，值为类别数
    for featVec in dataset:   # 统计各个类别的个数
        currentLabel = featVec[-1]
        if currentLabel not in labelCounts.keys():
            labelCounts[currentLabel] = 0
        labelCounts[currentLabel] += 1
    shannonEnt = 0.0   # 信息熵
    for key in labelCounts:
        prob = float(labelCounts[key])/numEntries
        shannonEnt -= prob * log(prob,2)
    return shannonEnt  # 信息熵

# 选出最好的数据集划分方式,即找出具有最大信息增益的特征
def chooseBestFeatureToSplit(dataSet):    #def 2
    numFeatures = len(dataSet[0])-1  # 特征数
    baseEntropy = calcShannonEnt(dataSet)  #计算数据集的香农熵
    bestInfoGain = 0.0; bestFeature = -1
    for i in range(numFeatures):
        featList = [example[i] for example in dataSet]  #第i列特征的所有特征的取值
        uniqueVals = set(featList)  # 去掉重复的特征，每个特征值都是唯一的
        newEntropy = 0.0
        for value in uniqueVals:
            subDataSet = splitDataSet(dataSet,i,value)
            prob = len(subDataSet)/float(len(dataSet))
            newEntropy += prob * calcShannonEnt(subDataSet)
        infoGain = baseEntropy - newEntropy  # 表示属性为value的信息增益
        if (infoGain > bestInfoGain):
            bestInfoGain = infoGain
            bestFeature = i
    return bestFeature  # 具有最大信息增益的特征

# 按照给定特征维数划分数据集,数据集中一行为一个样本
# def 3
def splitDataSet(dataSet,axis,value):   # axis可表示数据集的列，也就是特征为数，value表示特征的取值
    retDataSet = []
    for featVec in dataSet:
        if featVec[axis] == value:
            reducedFeatVec = featVec[:axis]    # 在数据集中去掉axis这一列
            reducedFeatVec.extend(featVec[axis+1:])
            retDataSet.append(reducedFeatVec)
    return retDataSet  # 表示去掉在axis中特征值为value的样本后而得到的数据集

# 当处理了所有属性，但是类标签依然不是唯一的，此时采用多数表决法决定该叶子节点的分类
def majorityCnt(classList):   # def 4
    classCount = {}
    for vote in classList:
        if vote not in classCount.keys():
            classCount[vote] = 0
        classCount += 1
    sortedClassCount = sorted(classCount.items(),key=lambda classCount: classCount[1],reverse = True)
    return sortedClassCount[0][0]

# 创建树
def createTree(dataSet,labels):   #  def 5
    classList = [example[-1] for example in dataSet]   #类别列表
    if classList.count(classList[0]) == len(classList):   # 如果类别完全相同就停止划分
        return classList[0]
    if (len(dataSet[0]) == 1):
        return majorityCnt(classList)
    bestFeat = chooseBestFeatureToSplit(dataSet)  # 选出最好的特征，也就是信息增益最大的特征
    bestFeatLabel = labels[bestFeat]
    myTree = {bestFeatLabel:{}}
    del(labels[bestFeat])   # 每划分一层，特征数目就会较少
    featValues = [example[bestFeat] for example in dataSet]    # 最好的特征的特征值
    uniqueVals = set(featValues)  #去掉重复的特征
    for value in uniqueVals:
        subLabels = labels[:]   # 减少后的特征名
        myTree[bestFeatLabel][value] = createTree(splitDataSet(dataSet,bestFeat,value),subLabels)
    return myTree

def createDateSet():
    dataSet = [[1,1,'yes'],[1,1,'yes'],[1,0,'no'],[0,1,'no'],[0,1,'no']]
    labels = ['no surfacing','flippers']   #属性名
    return dataSet,labels

myData,myLabel = createDateSet()
createTree(myData,myLabel)
print(createTree(myData,myLabel))
#print(chooseBestFeatureToSplit(myData))
# print(splitDataSet(myData,0,1))
# print(splitDataSet(myData,0,0))