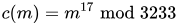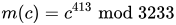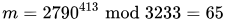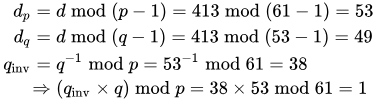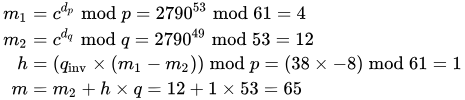Chinese_remainder_theorem
https://en.wikipedia.org/wiki/Chinese_remainder_theorem
中国剩余定理
https://en.wikipedia.org/wiki/RSA_(cryptosystem)
The public key is (n = 3233, e = 17). For a padded plaintext message m, the encryption function is
The private key is (n = 3233, d = 413). For an encrypted ciphertext c, the decryption function is
For instance, in order to encrypt m = 65, we calculate
To decrypt c = 2790, we calculate
Both of these calculations can be computed efficiently using the square-and-multiply algorithm for modular exponentiation. In real-life situations the primes selected would be much larger; in our example it would be trivial to factor n, 3233 (obtained from the freely available public key) back to the primes p and q. e, also from the public key, is then inverted to get d, thus acquiring the private key.
Practical implementations use the Chinese remainder theorem to speed up the calculation using modulus of factors (mod pq using mod p and mod q).
The values dp, dq and qinv, which are part of the private key are computed as follows:
Here is how dp, dq and qinv are used for efficient decryption. (Encryption is efficient by choice of a suitable d and e pair)
Chinese_remainder_theorem的更多相关文章
- CODEVS.3990.中国余数定理2(CRT)
题目链接 颓了一天 写个模板吧.. Chinese_Remainder_Theorem: MashiroSky.远航之曲 #include <cstdio> #include <cc ...
- 【10.4校内测试】【轮廓线DP】【中国剩余定理】【Trie树+博弈】
考场上几乎是一看就看出来轮廓线叻...可是调了两个小时打死也过不了手出样例!std发下来一对,特判对的啊,转移对的啊,$dp$数组竟然没有取max!!! 某位考生当场死亡. 结果下午又请了诸位dala ...
- NOIP数学相关模板整理
$O(n)$递推求逆元 #include<cstdio> #include<cstring> #include<algorithm> using namespace ...
- Chinese remainder theorem
https://en.wikipedia.org/wiki/Chinese_remainder_theorem http://planetmath.org/ChineseRemainderTheore ...
- 第三十三个知识点:Bellcore攻击是如何攻击使用CRT的RSA的?
第三十三个知识点:Bellcore攻击是如何攻击使用CRT的RSA的? 注意:这篇博客是由follow论密码计算中消除错误的重要性(On the importance of Eliminating E ...
随机推荐
- Zookeeper CLI
ZooKeeper命令行界面(CLI)用于与ZooKeeper集合进行交互以进行开发.它有助于调试和解决不同的选项. 要执行ZooKeeper CLI操作,首先打开ZooKeeper服务器(“bin/ ...
- 象“[]”、“.”、“->”这类操作符前后不加空格
象“[]”.“.”.“->”这类操作符前后不加空格. #include <iostream> #include <process.h> #include<stdio ...
- bootstrap -- css -- 文字、列表
文字 <small></small>:呈现小号字体效果. <big></big>:程序大号字体效果 <abbr></abbr>: ...
- struts2将数据通过Json格式显示于EasyUI-datagrid数据表格
1.搭建ssh开发环境 2.写好Dao.service等方法 3.建立DTO数据传输对象: package com.beichende.sshwork.user.web.dto; import jav ...
- openal资料转贴
地址:http://blog.sina.com.cn/s/blog_685b5b220100ukbp.html OpenAL简介 OpenAL(Open Audio Library)是专门负责3D定位 ...
- oracle查询一个用户下的所有表
select table_name from all_tables where owner_name=upper('scott'); 用户名一定要大写//
- mysqldump: command not found
原因:这是由于系统默认会查找/usr/bin下的命令,如果这个命令不在这个目录下,当然会找不到命令,我们需要做的就是映射一个链接到/usr/bin目录下,相当于建立一个链接文件.首先得知道mysql命 ...
- 【SJSB】 android-javascript开发框架
这是一个本人开发的android壳,作用就是为html5开发提供各种接口以调用native. 只是第一个版本,随笔以纪念.详细的说明和api都在 项目的readme中. 项目地址: https://g ...
- swift开发之--UISearchBar的使用/UISearchController的使用
记录下UISearchBar的基本用法,补充:ios 8.0以后,原来的UISearchDisplayController被官方废弃,建议使用UISearchController,下面就简单的记录下这 ...
- YARN 中的应用程序提交
YARN 中的应用程序提交 本节讨论在应用程序提交到 YARN 集群时,ResourceManager.ApplicationMaster.NodeManagers 和容器如何相互交互.下图显示了一个 ...