[luogu1447 NOI2010] 能量采集 (容斥原理)

传送门

Description

栋栋有一块长方形的地，他在地上种了一种能量植物，这种植物可以采集太阳光的能量。在这些植物采集能量后，栋栋再使用一个能量汇集机器把这些植物采集到的能量汇集到一起。

栋栋的植物种得非常整齐，一共有n列，每列有m棵，植物的横竖间距都一样，因此对于每一棵植物，栋栋可以用一个坐标(x, y)来表示，其中x的范围是1至n，表示是在第x列，y的范围是1至m，表示是在第x列的第y棵。

由于能量汇集机器较大，不便移动，栋栋将它放在了一个角上，坐标正好是(0, 0)。

能量汇集机器在汇集的过程中有一定的能量损失。如果一棵植物与能量汇集机器连接而成的线段上有k棵植物，则能 量的损失为2k + 1。例如，当能量汇集机器收集坐标为(2, 4)的植物时，由于连接线段上存在一棵植物(1, 2)，会产生3的能量损失。注意，如果一棵植物与能量汇集机器连接的线段上没有植物，则能量损失为1。现在要计算总的能量损失。

下面给出了一个能量采集的例子，其中n = 5，m = 4，一共有20棵植物，在每棵植物上标明了能量汇集机器收集它的能量时产生的能量损失。



在这个例子中，总共产生了36的能量损失。

Input

仅包含一行，为两个整数n和m。

Output

仅包含一个整数，表示总共产生的能量损失。

Sample Input

【样例输入1】

5 4

【样例输入2】

3 4

Sample Output

【样例输出1】

36

【样例输出2】

20

HINT

对于100%的数据：1 ≤ n, m ≤ 100,000。

Solution

主要是求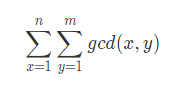

首先考虑n==m的情况，枚举最大公因数d ，那么 \(以d为最大公约数的点对数量=n/d以内互质的点对数量=phi(n/d)前缀和*2-1\) ，直接线性搞定~

再考虑n!=m的情况，仍然枚举最大公因数d，这次我们无法直接考虑以d为最大公约数的点对，但易知以d为公约数的点对共有 \((n/d)*(m/d)\) 个，只需利用容斥原理，将最大公约数为2d、3d、4d。。。。。。的全部减去即可

PS:若求出以后值为ans那么本题值为\(2*ans-n*m\)但这样会爆long long 所以要进行变形(见代码)

Code

//By Menteur_Hxy
#include<cstdio>
long long n,m,ans,f[100010];
int main() {
	scanf("%lld%lld",&n,&m);
	if(n>m) n^=m^=n^=m;
	for(register int i=n;i;i--) {
		f[i]=(long long)(n/i)*(m/i);
		for(register int j=i<<1;j<=n;j+=i) f[i]-=f[j];
		ans+=((i<<1)-1)*f[i];//防爆long long
	}
	printf("%lld",ans);
	return 0;
}