（CF#257)B. Jzzhu and Sequences

Jzzhu has invented a kind of sequences, they meet the following property:

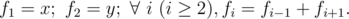
You are given x and y,
please calculate fn modulo 1000000007 (109 + 7).

Input

The first line contains two integers x and y (|x|, |y| ≤ 109).
The second line contains a single integer n (1 ≤ n ≤ 2·109).

Output

Output a single integer representing fn modulo 1000000007 (109 + 7).

Sample test(s)

input

2 3
3

output

1

input

0 -1
2

output

1000000006

Note

In the first sample, f2 = f1 + f3, 3 = 2 + f3, f3 = 1.

In the second sample, f2 =  - 1;  - 1 modulo (109 + 7) equals (109 + 6).

本来9点的CF，今天有学姐来，讲到了9点半，这题最后没注意坑点，最后判的时候还wa了，掉了100分，蛋疼中

#include<iostream>
#include<cstdio>
#include<cstring>
#include<algorithm>
using namespace std;
const int maxn=1100;
const int M=1000000007;
int a[maxn];
int main()
{
   int x,y,n;
   while(cin>>x>>y>>n)
   {
       a[1]=x;
       a[2]=y;
       int len=0,t;
       for(int i=3;;i++)
       {
           a[i]=a[i-1]-a[i-2];
           if(a[i]==a[2]&&a[i-1]==a[1]&&i>=4)
           {
               len=i-2;
               break;
           }
           if(i>=n)
             break;
       }
       if(len)
       {
//          cout<<"len:"<<len<<endl;
          t=(n-1)%len+1;
       }
       else
          t=n;
       if(a[t]>0)
          cout<<a[t]%M<<endl;
       else
       {
           while(a[t]<0)
             a[t]+=M;
           cout<<a[t]%M<<endl;
       }
   }
   return 0;
}

看了别人的想法，我的还是太狭隘了。我仅仅知道找规律，别人找的规律更详细。

#include<iostream>
#include<cstdio>
#include<cstring>
#include<algorithm>
using namespace std;
const int M=(1e9)+7;
int a[6];

int main()
{
    int x,y,n;
    while(cin>>x>>y>>n)
    {
        a[1]=(x+M)%M;
        a[2]=(y+M)%M;
        a[3]=(a[2]-a[1]+M)%M;
        a[4]=(-x+M)%M;
        a[5]=(-y+M)%M;
        a[0]=(a[1]-a[2]+M)%M;
        cout<<(a[n%6]+M)%M<<endl;
    }
}