图：

图中涉及的定义：

有向图：

顶点之间的相关连接具有方向性；

无向图：

顶点之间相关连接没有方向性；

完全图：

若G是无向图，则顶点数n和边数e满足：0<=e<=n(n-1)/2,当e=n(n-1)/2时，称之为完全无向图；若G是有向图，则0<=e<=n(n-1)；当e=n(n-1)时，称之为完全有向图；即此时图中边数最多；

顶点的度：

无向图中定义为关联顶点的边数，有向图中分入度和出度；度D(G)和边数e满足关系：2*e=D(G)，即边数的两倍等于图中度数和；

图的实现：

邻接矩阵实现图：

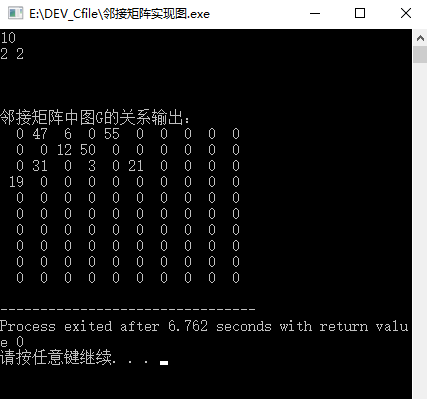
#include<cstdio>
#include<cstdlib>
#include<algorithm>
#include<iostream>
#define MAX_SIZE 10005
using namespace std;
int tmp[MAX_SIZE][MAX_SIZE];                 		 //由于数组可能会比较大，定义在main里面可能会爆，所以先定义在全局； 
typedef struct agraph* Graph;
typedef struct agraph
{
	int n;                                  		//顶点数
	int e;                                  		//边数
	int a[MAX_SIZE][MAX_SIZE];
}Agraph;
Graph GraphInit(int n,Graph G)						// 对图G的初始化；
{
	G->n=n;
	G->e=0;
	return G;
}
void GraphAdd(int i,int j,int val,Graph G)			//插入顶点之间的连接关系；
{
	G->a[i][j]=val;G->e++;
}
void GraphDelete(int i,int j,Graph G)				//删除顶点之间的连接关系；
{
	G->a[i][j]=0;G->e--;
}
int OutDegree(int i,Graph G)
{
	int j,sum=0;
	for(j=1;j<G->n;j++)
	{
		if(G->a[i][j]!=0)sum++;
	}
	return sum;
}
int InDegree(int i,Graph G)
{
	int j,sum=0;
	for(j=1;j<=G->n;j++)
	{
		if(G->a[j][i]!=0)sum++;
	}
	return sum;
}
void GraphOut(Graph G)
{
	int i,j;
	for(i=1;i<=G->n;i++)
	{
		for(j=1;j<=G->n;j++)
			printf("%3d",G->a[i][j]);
		printf("\n");
	}
}
int main()
{
	int i,j,n;
	scanf("%d",&n);
	Graph G=new Agraph;
	G=GraphInit(n,G);
	GraphAdd(1,3,6,G);
	GraphAdd(1,5,55,G);
	GraphAdd(2,3,12,G);
	GraphAdd(2,4,50,G);
	GraphAdd(3,4,3,G);
	GraphAdd(1,2,47,G);
	GraphAdd(3,6,21,G);
	GraphAdd(3,2,31,G);
	GraphAdd(4,1,19,G);
	printf("%d %d\n",InDegree(2,G),OutDegree(2,G));
	printf("\n\n\n");
	printf("邻接矩阵中图G的关系输出：\n");
	GraphOut(G);
	return 0;
}

输出截图：

邻接表实现图：

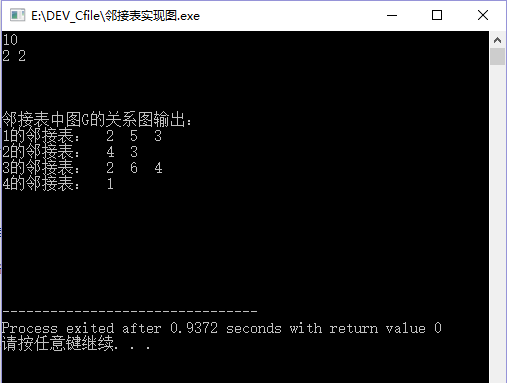
#include<cstdio>
#include<cstdlib>
#include<iostream>
using namespace std;
typedef struct anode* Node;										//可以看成是建立一条边；
typedef struct anode
{
	int v;														//边的另一个顶点；
	int val; 													//边权；
	Node next;													//邻接表指针；
}Anode;
typedef struct agraph* Graph;
typedef struct agraph
{
	int n;
	int edges;
	Node *nodes;
}Agraph;
Node NewNext(int v,int val,Node next)							//新建一个节点建立边的连接关系；
{
	Node x=new Anode;
	x->v=v;
	x->val=val;
	x->next=next;
	return x;
}
Graph GraphInit(int  n,Graph G)									//对图G的初始化；
{
	int i;
	G->n=n;
	G->edges=0;
	G->nodes=(Node*)malloc((n+1)*sizeof(Node));
	for(i=0;i<=n;i++)
	{
		G->nodes[i]=0;
	}
	return G;
}
void GraphAdd(int i,int j,int val,Graph G)
{
	G->nodes[i]=NewNext(j,val,G->nodes[i]);						//相当于i的邻接顶点不断增加时，其邻接表从表头加入，先加入的关系不断后移；
	G->edges++;
}
void GraphDelete(int i,int j,Graph G)
{
	Node p,q;
	p=G->nodes[i];
	if(p->v==j)
	{
		G->nodes[i]=p->next;
		free(p);
	}
	else
	{
		while(p&&p->next->v!=j)p=p->next;
		if(p)
		{
			q=p->next;
			p->next=q->next;
			free(q);
		}
	}
	G->edges--;
}
int InDegree(int i,Graph G)
{
	int j,sum=0;
	for(j=1;j<=G->n;j++)
	{
		/*判断当前有向图G中的边（i,j）是否存在*/
		Node p=G->nodes[i];
		while(p&&p->v!=j)p=p->next;
		if(p)sum++;
	}
	return sum;
}
int OutDegree(int i,Graph G)
{
	Node p=G->nodes[i];
	int sum=0;
	while(p)
	{
		sum++;
		p=p->next;
	}
	return sum;
}
void GraphOut(Graph G)
{
	Node p;
	int i;
	for(i=1;i<=G->n;i++)
	{
		if(G->nodes[i])printf("%d的邻接表：",i);
		p=G->nodes[i];
		while(p)
		{
			printf("%3d",p->v);
			p=p->next;
		}
		printf("\n");
	}
}
int main()
{
	int i,j,n;
	scanf("%d",&n);
	Graph G=new Agraph;
	G=GraphInit(n,G);
	GraphAdd(1,3,6,G);
	GraphAdd(1,5,55,G);
	GraphAdd(2,3,12,G);
	GraphAdd(2,4,50,G);
	GraphAdd(3,4,3,G);
	GraphAdd(1,2,47,G);
	GraphAdd(3,6,21,G);
	GraphAdd(3,2,31,G);
	GraphAdd(4,1,19,G);
	printf("%d %d\n",InDegree(2,G),OutDegree(2,G));
	printf("\n\n\n");
	printf("邻接表中图G的关系图输出：\n");
	GraphOut(G);
	return 0;
}

输出截图：

图的遍历：

图的遍历一般有两种方法：

1、广度优先搜索；2、深度优先搜索；

#include<cstdio>
#include<cstdlib>
#include<algorithm>
#include<iostream>
#include<queue>
#define MAX_SIZE 10005
using namespace std;
int vis[10005]={0};
int cnt;
int tmp[MAX_SIZE][MAX_SIZE];                 		 //由于数组可能会比较大，定义在main里面可能会爆，所以先定义在全局； 
typedef struct agraph* Graph;
typedef struct agraph
{
	int n;                                  		//顶点数
	int e;                                  		//边数
	int a[MAX_SIZE][MAX_SIZE];
}Agraph;
Graph GraphInit(int n,Graph G)						// 对图G的初始化；
{
	G->n=n;
	G->e=0;
	return G;
}
void GraphAdd(int i,int j,int val,Graph G)			//插入顶点之间的连接关系；
{
	G->a[i][j]=val;G->e++;
}
void GraphDelete(int i,int j,Graph G)				//删除顶点之间的连接关系；
{
	G->a[i][j]=0;G->e--;
}
int OutDegree(int i,Graph G)
{
	int j,sum=0;
	for(j=1;j<G->n;j++)
	{
		if(G->a[i][j]!=0)sum++;
	}
	return sum;
}
int InDegree(int i,Graph G)
{
	int j,sum=0;
	for(j=1;j<=G->n;j++)
	{
		if(G->a[j][i]!=0)sum++;
	}
	return sum;
}
void GraphOut(Graph G)
{
	int i,j;
	for(i=1;i<=G->n;i++)
	{
		for(j=1;j<=G->n;j++)
			printf("%3d",G->a[i][j]);
		printf("\n");
	}
}
/*图的遍历：广度优先搜索*/
void bfs(Graph G,int i)
{
	int j;
	queue<int>q;
	q.push(i);														//从i顶点开始当前的搜索，即用顶点i初始化队列q；
	vis[i]=cnt++;													//vis数组储存的是编号为j的这个顶点被访问时的序号；即第几个被访问到的顶点；
	while(!q.empty())
	{
		i=q.front();
		q.pop();
		for(j=1;j<=G->n;j++)										//即对每次的i的相邻的未被访问过的顶点进行访问（符合广度优先搜索的由近到远搜索）
		{
			if((G->a[i][j])&&(vis[j]==0))
			{
				q.push(j);
				vis[j]=cnt++;
			}
		}
	}
}
void GraphSearchByBfs(Graph G)
{
	int i;
	cnt=1;
	for(i=1;i<=G->n;i++)
	{
		if(vis[i]==0)
			bfs(G,i);										//n个顶点中可能存在多个联通块，对其做一次循环之后可以保证将图中的所有的顶点都访问到；
	}
}
//上述邻接矩阵实现的图的广度优先搜索遍历因为在搜索时需要确保对所有的顶点都访问，因此所需要的时间为O(n*n)； 
/*图的遍历：深度优先搜索*/
void dfs(Graph G,int i)										//邻接矩阵实现的图的深搜
{
	int j;
	vis[i]=cnt++;
	for(j=1;j<=G->n;j++)
	{
		if(G->a[i][j])
		{
			if(vis[j]==0)dfs(G,j);							//即递归走到尽头才停止这一次的搜索；
		}
	}
}
/*这段邻接表深搜函数函数适用的是邻接表实现的图，在此无效*/
//void dfs2(Graph G,int i)
//{
//	Node p;
//	vis[i]=cnt++;
//	for(p=G->nodes[i];p;p=p->next)
//	{
//		if(vis[p->v]==0)
//			dfs(G,p->v);
//	}
//}
void GraphSearchByDfs(Graph G)
{
	int i;
	cnt=1;
	for(i=1;i<=G->n;i++)
	{
		if(vis[i]==0)
			dfs(G,i);										//n个顶点中可能存在多个联通分支，对其做一次循环之后可以保证将图中的所有的路径都访问到；
	}
}
int main()
{
	int i,j,n;
	scanf("%d",&n);
	Graph G=new Agraph;
	G=GraphInit(n,G);
	GraphAdd(1,3,6,G);
	GraphAdd(1,5,55,G);
	GraphAdd(2,3,12,G);
	GraphAdd(2,4,50,G);
	GraphAdd(3,4,3,G);
	GraphAdd(1,2,47,G);
	GraphAdd(3,6,21,G);
	GraphAdd(3,2,31,G);
	GraphAdd(4,1,19,G);
	GraphAdd(7,3,12,G);
	GraphAdd(2,9,1,G);
	GraphAdd(3,8,47,G);
	GraphAdd(7,9,99,G);
	GraphAdd(7,10,11,G);
	GraphAdd(9,8,23,G);
	printf("%d %d\n",InDegree(2,G),OutDegree(2,G));
	printf("\n\n\n");
	printf("邻接表中图G的关系图输出：\n\n");
	GraphOut(G);
//	printf("\n\n");
//	printf("对图进行遍历，广度优先搜索输出：\n\n");
//	GraphSearchByBfs(G);
//	for(i=1;i<=n;i++)
//		printf("%d是第%d个遍历到的顶点\n\n",i,vis[i]);
	printf("\n\n");
	printf("对图进行遍历，深度优先搜索输出：\n\n");
	GraphSearchByDfs(G);
	for(i=1;i<=n;i++)
		printf("%d是第%d个遍历到的顶点\n\n",i,vis[i]);
	return 0;
}

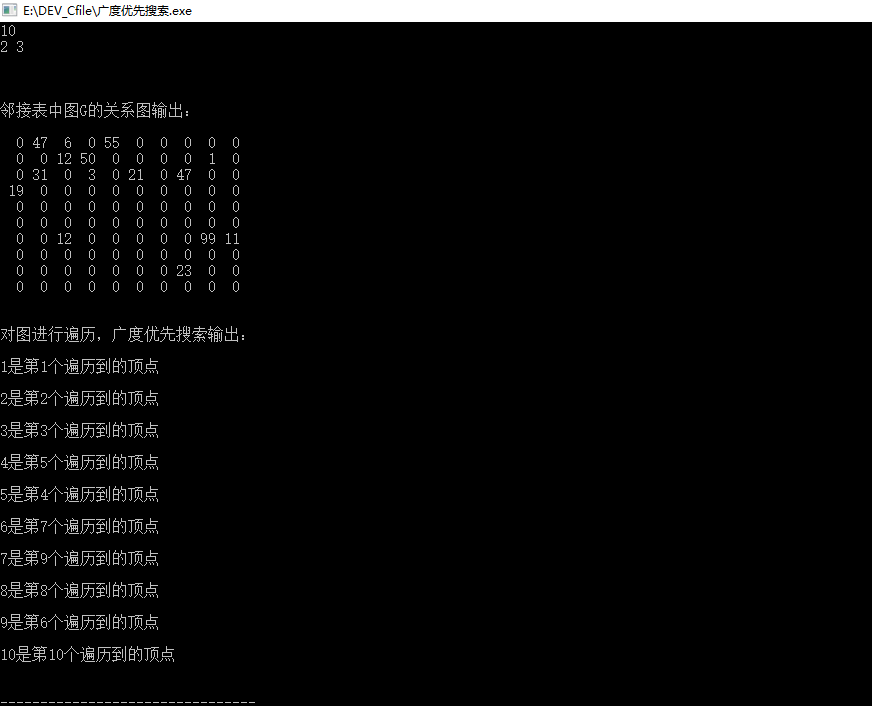
1、广度优先搜索：

基本思想：从图中的某个顶点i出发，在访问了顶点i之后，接着就尽可能的先横向搜索i的邻接顶点，在一次访问过i的各个未被访问过的邻接顶点之后，分别从这些邻接顶点出发，递归以广度优先方式搜索图中的其他顶点，直至图中的所有顶点都被访问到为止；即以i为起始顶点，由近到远（即路径长度为1,2,3，.....）依次访问和顶点i有路相通的顶点;

输出结果：

2、深度优先搜索：

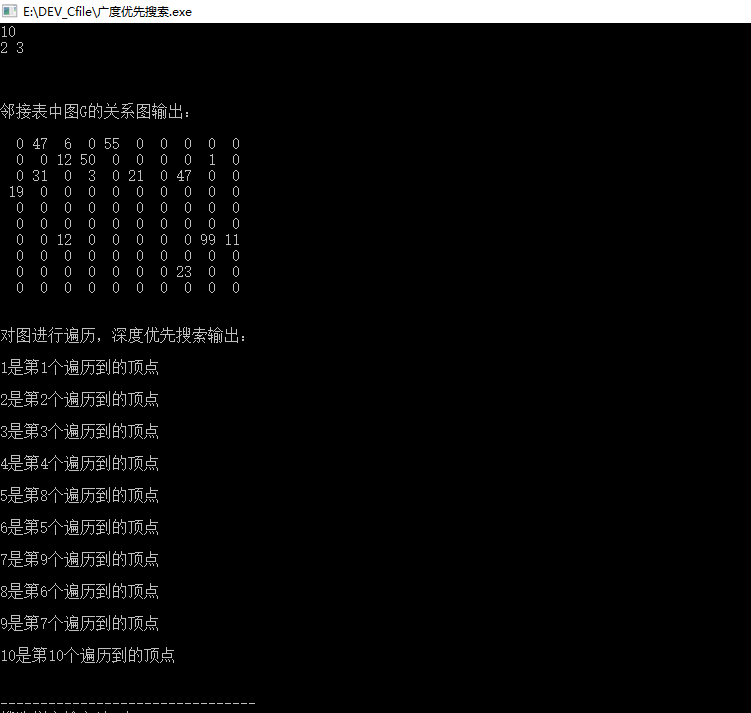
从i开始搜索，标记i为已访问再递归的用深度优先搜索依次搜索i的每一个未被访问的邻接顶点，如果从i出发有路可达的顶点都已被访问过，则从i开始的搜索过程结束；此时，如果图中海油未被访问的节点，则再任选一个并从该节点开始做新的搜索；直至图中所有的节点都被访问过为止；

输出结果：

图的实际问题应用：

最短路径问题：1、单源最短路径；2、所有顶点对之间的最短路径；

单源最短路径(Dijkstra算法/Bellman-Ford算法)：

Dijktra(不能存在负权边):

V是赋权有向图，设置一个集合S并不断作贪心算法扩充该集合，其中的顶点当且仅当源到该顶点的最短路径已知；用dist[]数组记录当前每个顶点所对应的最短特殊路径长度（特殊路径：从源到顶点u且中间只经过S中顶点的路径称为从源到u的特殊路径）。该算法每次从V-S中取出具有最短路径长度的顶点u，将其添加到S中，同时对数组dist作必要的修改，当S中包含了V中所有顶点，dist就记录了从源到其他所有顶点的最短路径长度；

Bellman-Ford：

对图中除源顶点s外的任一顶点u，依次构造

从s到u的最短路径长度序列dist1[u],dist2[u],...,dist n-1[u].其中dist i[u]表示从s到u的最多经过i条边的最短路径长度；若G中没有从源可达的负权圈，则从s到u的最多有n-1条边；因此，dist n-1[u]就是从s到u的最短路径长度；

实现时：

用ub[]数组记录顶点的最短路径长度更细状态，count[]数组记录顶点的最短路径长度更新次数，队列que[]存储最短路径更新过的顶点，算法依次从que中取出待更新的顶点u，按照计算dist i[u]的递归式进行计算，一旦发现存在顶点k有count[k]>n，说明图G中有一个从k出发的负权圈，算法终止，否则，当队列que为空时，算法得到图G的各顶点的最短路径长度；

具体题目应用代码：后续详细复习补上；

所有顶点对之间的最短路径（floyd算法）：

Dijsktra * n：

每次以一个顶点为源，重复执行Dijkstra算法n次；时间复杂度为O（n* n *n）;

Floyd：

设置一个n*n的矩阵c，初始时c[i][j]=a[i][j]；a是权值数组；在矩阵c上做n次迭代，经k次迭代后，c[i][j]值是从顶点i到顶点j且中间不经过编号大于k的顶点的最短路径长度。做迭代时，公式：c[i][j] = min{ a[i][j] , c[i][k]+a[k][j] };

第十一次作业：

1、（给定一个图，求图中所有顶点对之间的最短路径长度，用Floyd算法实现）


            #include<iostream>
#include<cstdio>
#include<cstring>
#define INF 0x3f3f3f3f
#define MAX 405
using namespace std;
int pre[MAX][MAX],dist[MAX][MAX];
void Floyd(int n,int gra[][MAX])
{
	int i,j,k;
	for(i=1;i<=n;i++)
	{
		for(j=1;j<=n;j++)
		{
			dist[i][j]=gra[i][j];pre[i][j]=j;
		}
	}
	for(k=1;k<=n;k++)
	{
		for(i=1;i<=n;i++)
		{
			for(j=1;j<=n;j++)
			{
				if(dist[i][k]!=INF&&dist[k][j]!=INF&&dist[i][k]+dist[k][j]<dist[i][j])
				{
					dist[i][j]=dist[i][k]+dist[k][j];
					pre[i][j]=pre[i][k];
				}
			}
		}
	}
}
int gra[MAX][MAX];
int main()
{
	int n,m,i,j,k;
	int u,v,val,tmp,que;
	scanf("%d%d",&n,&m);
	for(i=0;i<=n;i++)
	{
		for(j=0;j<=n;j++)
		{
			gra[i][j]=(i==j?0:INF);
		}
	}
	for(i=0;i<m;i++)
	{
		scanf("%d%d%d",&u,&v,&val);
		gra[u][v]=gra[v][u]=val;
	}
	Floyd(n,gra);
	scanf("%d",&que);
	for(i=0;i<que;i++)
	{
		scanf("%d%d",&u,&v);
		if(dist[u][v]!=INF)
			printf("%d\n",dist[u][v]);
		else printf("-1\n");
	}
	return 0;
}

2、（判断图中是否存在负权圈--深搜做法：但是要会开类似三维数组vector<pair<int,int>>vv[2005];）

#include<stdio.h>
#include<vector>
#include<memory.h>
using namespace std;
bool vis[2005];
vector<pair<int,int> >vv[2005];
int n,m,s;
bool flag=false;
int dis[2005];
void dfs(int pos)
{
	if(flag) return;
	vis[pos]=true;
	vector<pair<int,int> >::iterator it;
	for(it=vv[pos].begin();it!=vv[pos].end();it++)
	{   int to=it->first;
		if(dis[to]>dis[pos]+it->second)
		{
			dis[to]=dis[pos]+it->second;
		if(vis[to]) {
		flag=true;return;}
		else
		{
			dfs(to);
		}
       	}
	}
}
int main()
{
	scanf("%d%d",&n,&m);
	int  i,j;
	memset(vis,false,sizeof(vis));
	memset(dis,0,sizeof(dis));
	for(i=1;i<=n;i++) vv[i].clear();
	for(i=1;i<=m;i++)
	{
		int u,v,w;
		scanf("%d%d%d",&u,&v,&w);
		vv[u].push_back(make_pair(v,w));
	}
	scanf("%d",&s);
	dis[s]=0;
	dfs(s);
	if(flag) printf("EL PSY CONGROO");
	else printf("ttt");
}

ADT图及图的实现及图的应用的更多相关文章

用rose画UML图（用例图，活动图）
用rose画UML图(用例图,活动图) 首先,安装rose2003,电脑从win8升到win10以后,发现win10并不支持rose2003的安装,换了rose2007以后,发现也不可以. 解决途径: ...
相机拍的图，电脑上画的图，word里的文字，电脑屏幕，手机屏幕，相机屏幕显示大小一切的一切都搞明白了！
相机拍的图,电脑上画的图,word里的文字,电脑屏幕,手机屏幕,相机屏幕显示大小一切的一切都搞明白了! 先说图片X×dpi=点数dotX是图片实际尺寸,简单点,我们只算图片的高吧,比如说拍了张图片14 ...
各种图（流程图，思维导图，UML，拓扑图，ER图）简介
来源于:http://www.cnblogs.com/jiqing9006/p/3344221.html 流程图 1.定义:流程图是对过程.算法.流程的一种图像表示,在技术设计.交流及商业简报等领域有 ...
UML精粹5 - 状态图，活动图，通信图，组合结构，组件图，协作，交互概述图，时间图
状态机图state machine diagram 下面是状态图的一个例子(一个城堡中的秘密保险箱的控制面板). 转换transition包括3个部分:trigger-signature [guard ...
Shader中贴图知识汇总：漫反射贴图、凹凸贴图、高光贴图、 AO贴图、环境贴图、光照纹理及细节贴图
原文过于冗余,精读后做了部分简化与测试实践,原文地址:http://www.j2megame.com/html/xwzx/ty/2571.html http://www.cnblogs.com/z ...
uml的图与代码的转换——类图
Uml是我们经常使用的统一建模语言或称标准建模语言.它的图是如何和代码对应的呢?下面我们就来就这个问题讨论一下: 首先是类:uml中的类图是这样的在这个图中,我们可以看出,这个类图总共分了三行,第一 ...
【转】各种图（流程图，思维导图，UML，拓扑图，ER图）简介
原文地址:各种图(流程图,思维导图,UML,拓扑图,ER图)简介流程图 1.定义:流程图是对过程.算法.流程的一种图像表示,在技术设计.交流及商业简报等领域有广泛的应用. 2.案例 3.计算机语言只 ...
点9图 Android设计中如何切图.9.png
转载自:http://blog.csdn.net/buaaroid/article/details/51499516 本文主要介绍如何制作切图.9.png(点9图),另一篇姊妹篇文章Android屏 ...
Lodop如何设置预览后导出带背景的图，打印不带背景图
Lodop中的ADD_PRINT_SETUP_BKIMG,可以加载上背景图,该背景图在预览的时候可以显示也可以不显示,打印可以打印出来也可以不打印出来.一般套打,都是不打印背景图的,比如一些快递的快递 ...
vue 弹性布局实现长图垂直居上，短图垂直居中
vue 弹性布局实现长图垂直居上,短图垂直居中大致效果如下图,只考虑垂直方向.长图可以通过滚动条看,短图居中效果,布局合理 html代码(vue作用域内): <div class=" ...

随机推荐

PTA-括号问题
括号问题作者: 李廷元单位: 中国民用航空飞行学院时间限制: 400 ms 内存限制: 64 MB 代码长度限制: 16 KB 问题描述给定一串字符,不超过100个字符,可能包括括号.数字.字 ...
Verilog中使用'include实现参数化设计
前段时间在FPGA上用Verilog写了一个多端口以太网的数据分发模块,因为每个网口需要独立的MAC地址和IP地址,为了便于后期修改,在设计中使用parameter来定义这些地址和数据总线的位宽等常量 ...
托管代码编写mssql存储过程
参考:http://wenku.it168.com/d_000642903.shtml 打开vs,创建数据库项目,添加新项,选择sql clr c#, 选择存储过程. 样例: [Microsoft.S ...
兼容性/pollyfill/shim/渐进增强／优雅降级
http://ued.ctrip.com/blog/browser-compatibility-testing-tools-in-firefox-compatibility-detector.html ...
【BZOJ1047】[HAOI2007]理想的正方形
[BZOJ1047][HAOI2007]理想的正方形题面 bzoj 洛谷题解二维\(st\)表,代码是以前的 #include<iostream> #include<cstdi ...
CF97C Winning Strategy
CF97C Winning Strategy 洛咕(题意应该快传上去了) 这题好玄学鸭...都不知道为啥是对的设\(f[i][j]\)表示打了i轮比赛,有j个参加了一次的人,直接枚举有几个参加了转移 ...
JavaScript——引用类型之数组
前言之前本菜打算在写完基本类型后写引用类型Object的,因为Object是引用类型的基础,其他的引用类型也是以Object为根本.只是关于对象的基本认识与简单操作确实可写的不多,打算之后与原型.原 ...
Docker Manager for Docker Swarm deploy
一.Swarm概述 Swarm是Docker公司在2014年12月初发布的一套较为简单的工具,用来管理Docker集群,它将一群Docker宿主机变成一个单一的,虚拟的主机.Swarm使用标准的Doc ...
vue-scroller实现vue单页面的上拉加载和下拉刷新问题
在vue中如何简单的实现页面的上拉加载和下拉刷新,在这里我推荐使用vue-scrolle插件. vue-scrolle的基本使用方法: 1.下载 npm i vue-scroller -D 2.导包 ...
ELK环境搭建
ELK环境搭建 1. Virtualbox/Vagrant安装 41.1. Virtualbox安装 41.2. Vagrant安装 41.2.1. 简述 41.2.2. Vagrant box 41 ...

ADT图及图的实现及图的应用

图：