【NOI2016】区间

目链接：http://uoj.ac/problem/222

在数轴上有 n 个闭区间 [l1,r1],[l2,r2],...,[ln,rn]。现在要从中选出 m 个区间，使得这 m 个区间共同包含至少一个位置。换句话说，就是使得存在一个 x ，使得对于每一个被选中的区间 [li,ri]，都有 li≤x≤ri。

对于一个合法的选取方案，它的花费为被选中的最长区间长度减去被选中的最短区间长度。区间 [li,ri]的长度定义为 ri−li，即等于它的右端点的值减去左端点的值。

求所有合法方案中最小的花费。如果不存在合法的方案，输出 −1 。

输入格式

第一行包含两个正整数 n,m，用空格隔开，意义如上文所述。保证 1≤m≤n。

接下来 n 行，每行表示一个区间，包含用空格隔开的两个整数 li 和 ri 为该区间的左右端点。

输出格式

只有一行，包含一个正整数，即最小花费。

样例一

input

6 3
3 5
1 2
3 4
2 2
1 5
1 4

output

2

explanation

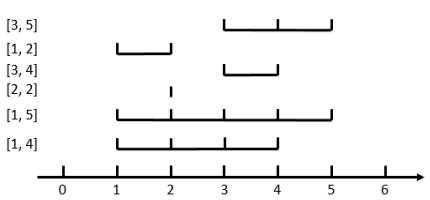
如图，当 n=6, m=3n=6, m=3 时，花费最小的方案是选取 [3,5][3,5] 、[3,4][3,4] 、[1,4][1,4] 这三个区间，他们共同包含了 44 这个位置，所以是合法的。其中最长的区间是 [1,4][1,4] ，最短的区间是 [3,4][3,4] ，所以它的花费是 (4−1)−(4−3)=2(4−1)−(4−3)=2 。

限制与约定

所有测试数据的范围和特点如下表所示：

测试点编号	n	m	li,ri
1	20	9	0≤li≤ri≤1000
2		10
3	199	3	0≤li≤ri≤100000
4	200
5	1000	2
6	2000
7	199	60	0≤li≤ri≤5000
8	200	50
9			0≤li≤ri≤10^9
10	1999	500	0≤li≤ri≤5000
11	2000	400
12		500	0≤li≤ri≤10^9
13	30000	2000	0≤li≤ri≤100000
14	40000	1000
15	50000	15000
16	100000	20000
17	200000		0≤li≤ri≤10^9
18	300000	50000
19	400000	90000
20	500000	200000

时间限制：3s

空间限制：256MB

题解

首先对li,ri离散化。

如样例

3 5
1 2
3 4
2 2
1 5
1 4

经排序后——1 1 1 2 2 2 3 3 4 4 5 5。(3,5)就变成了(7,11)这样l,r就变成<=500000了。

将每条线段按长度排个序，变成！

2 2

1 2

3 4

3 5

1 4

1 5

接下来，维护一个双指针(two pointer)如

l

1 2 3 4 5 6(线段编号)

r

不断向右移动r直到有个点出现的次数>m为止如

l

1 2 3 4 5 6

r——>r

记录答案

再不断向右移动l，直到没有一个位置出现的次数>m如

l—->l

1 2 3 4 5 6

r——>r

记录答案，以此类推，直到r>n为止。

放代码跑

#include <cstdio>
#include <algorithm>
using namespace std;
struct data{int l,r,len;}a[];
struct tree{int l,r,max,lazy;}T[];
int b[],num,i,j,k,n,m,x,y,t;
bool cmp(const data&a,const data&b){return a.len<b.len;}
int find(int x){
    int l=,r=num,ans;
    while (l<=r){
        int mid=(l+r)>>;
        if (b[mid]>=x)ans=mid,r=mid-;else l=mid+;
    }
    return ans;
}
void build(int i,int l,int r){
    T[i].l=l;T[i].r=r;T[i].max=;
    if (l==r)return;
    build(i*,l,(l+r)>>);build(i*+,((l+r)>>)+,r);
}
void pushdown(int i){
    if (T[i].lazy){
        T[i*].max+=T[i].lazy;T[i*+].max+=T[i].lazy;
        T[i*].lazy+=T[i].lazy;T[i*+].lazy+=T[i].lazy;
        T[i].lazy=;
    }
}
void pushup(int i){T[i].max=max(T[i*].max,T[i*+].max);}
void change(int i,int l,int r,int v){
    if (T[i].l==l&&T[i].r==r){T[i].max+=v;T[i].lazy+=v;return;}
    pushdown(i);
    int mid=(T[i].l+T[i].r)>>;
    if (r<=mid)change(i*,l,r,v);
    else if (l>mid)change(i*+,l,r,v);
    else {change(i*,l,mid,v);change(i*+,mid+,r,v);}
    pushup(i);
}
int main(){
    scanf("%d%d",&n,&m);
    for (i=;i<=n;i++){
        scanf("%d%d",&x,&y);
        a[i].l=x;a[i].r=y;a[i].len=y-x;
        b[++num]=x;b[++num]=y;
    }
    sort(a+,a++n,cmp);sort(b+,b++num);
    for (i=;i<=n;i++)a[i].l=find(a[i].l),a[i].r=find(a[i].r);
    build(,,num);
    int l=,r=,ans=;
    while(l<=n&&r<=n){
        while (T[].max<m&&r<=n){change(,a[r].l,a[r].r,);r++;}
        if (T[].max>=m)ans=min(ans,a[r-].len-a[l].len);
        if (r>n)break;
        change(,a[l].l,a[l].r,-);l++;
    }
    printf("%d\n",ans==?-:ans);
    return ;
}