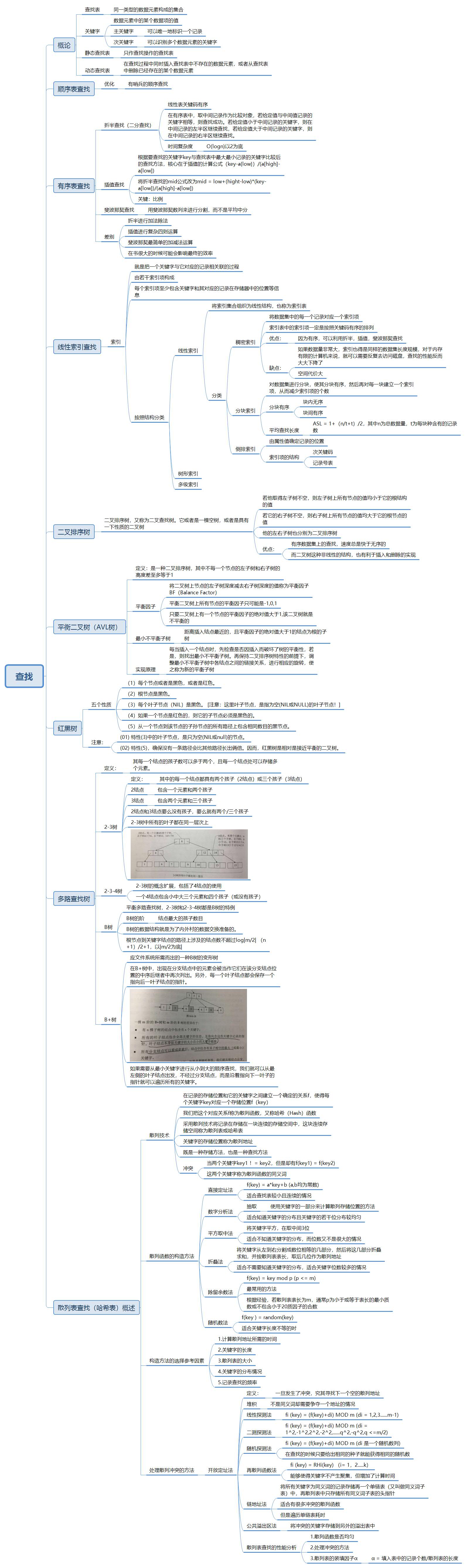
Chapter 8(查找)
1.二分查找和插值查找
//************************Search.h***********************************
#ifndef SEARCH_H
#define SEARCH_H
#include <stdio.h>
#include <stdlib.h>
int BiSearch(int array[],int n,int key);
int IVSearch(int array[],int n,int key);
int FibSearch(int array[],int n,int key);
#endif //SEARCH_H
//************************Search.c*************************************
#include "Search.h"
//折半查找
int BiSearch(int array[],int n,int key)
{
if(NULL == array)return -1;
int left = 0;
int right= n-1;
int mid = (left+right)/2;
while(left <= right)
{
if(array[mid] == key)
{
return mid;
}
else if(array[mid] > key)
{
right = mid-1;
}
else if(array[mid] < key)
{
left = mid+1;
}
mid = (left+right)/2;
}
return -1;
}
//插值查找
int IVSearch(int array[],int n,int key)
{
if(NULL == array)return -1;
int left = 0;
int right= n-1;
int mid = left+(right-left)*(key-array[left])/(array[right]-array[left]);
while(left <= right)
{
if(array[mid] == key)
{
return mid;
}
else if(array[mid] > key)
{
right = mid-1;
}
else if(array[mid] < key)
{
left = mid+1;
}
mid = left+(right-left)*(key-array[left])/(array[right]-array[left]);
}
return -1;
}
int FibSearch(int array[],int n,int key)
{
int F[] = {1,1,2,3,5,8,13,21,34,55,89};
int left = 0;
int right= n-1;
int mid;
int k = 0;
while(n>F[k]-1)
{
k++;
}
for(int i=n;i < F[k])
}
//************************SearchTest.c*************************************
#include "Search.h"
int main()
{
int a[10] = {1,16,24,35,47,59,62,73,88,99};
int key = 62;
printf("position: %d \n",BiSearch(a,10,key));
printf("position: %d \n",IVSearch(a,10,key));
}110
1
//************************Search.h***********************************
2
#ifndef SEARCH_H
3
#define SEARCH_H
4
5
#include <stdio.h>
6
#include <stdlib.h>
7
8
int BiSearch(int array[],int n,int key);
9
10
int IVSearch(int array[],int n,int key);
11
12
int FibSearch(int array[],int n,int key);
13
14
15
16
#endif //SEARCH_H
17
18
19
//************************Search.c*************************************
20
#include "Search.h"
21
22
23
//折半查找
24
int BiSearch(int array[],int n,int key)
25
{
26
if(NULL == array)return -1;
27
int left = 0;
28
int right= n-1;
29
int mid = (left+right)/2;
30
31
while(left <= right)
32
{
33
if(array[mid] == key)
34
{
35
return mid;
36
}
37
else if(array[mid] > key)
38
{
39
right = mid-1;
40
}
41
else if(array[mid] < key)
42
{
43
left = mid+1;
44
}
45
mid = (left+right)/2;
46
}
47
return -1;
48
}
49
50
51
//插值查找
52
int IVSearch(int array[],int n,int key)
53
{
54
if(NULL == array)return -1;
55
int left = 0;
56
int right= n-1;
57
int mid = left+(right-left)*(key-array[left])/(array[right]-array[left]);
58
59
while(left <= right)
60
{
61
if(array[mid] == key)
62
{
63
return mid;
64
}
65
else if(array[mid] > key)
66
{
67
right = mid-1;
68
}
69
else if(array[mid] < key)
70
{
71
left = mid+1;
72
}
73
mid = left+(right-left)*(key-array[left])/(array[right]-array[left]);
74
}
75
return -1;
76
}
77
78
79
80
int FibSearch(int array[],int n,int key)
81
{
82
int F[] = {1,1,2,3,5,8,13,21,34,55,89};
83
84
85
int left = 0;
86
int right= n-1;
87
int mid;
88
89
int k = 0;
90
while(n>F[k]-1)
91
{
92
k++;
93
}
94
for(int i=n;i < F[k])
95
96
}
97
98
99
//************************SearchTest.c*************************************
100
#include "Search.h"
101
102
103
int main()
104
{
105
int a[10] = {1,16,24,35,47,59,62,73,88,99};
106
int key = 62;
107
108
printf("position: %d \n",BiSearch(a,10,key));
109
printf("position: %d \n",IVSearch(a,10,key));
110
}
2.斐波那契查找
#include <stdio.h>
#include <stdlib.h>
#define MAXN 20
/*
*产生斐波那契数列
* */
void Fibonacci(int *f)
{
int i;
f[0] = 1;
f[1] = 1;
for(i = 2;i < MAXN; ++i)
f[i] = f[i - 2] + f[i - 1];
}
/*
* 查找
* */
int Fibonacci_Search(int *a, int key, int n)
{
int i, low = 0, high = n - 1;
int mid = 0;
int k = 0;
int F[MAXN];
Fibonacci(F);
while(n > F[k] - 1) //计算出n在斐波那契中的数列
++k;
for(i = n;i < F[k] - 1;++i) //把数组补全
a[i] = a[high];
while(low <= high)
{
mid = low + F[k-1] - 1; //根据斐波那契数列进行黄金分割
if(a[mid] > key)
{
high = mid - 1;
k = k - 1;
}
else if(a[mid] < key)
{
low = mid + 1;
k = k - 2;
}
else
{
if(mid <= high) //如果为真则找到相应的位置
return mid;
else
return -1;
}
}
return 0;
}
int main()
{
int a[MAXN] = {5,15,19,20,25,31,38,41,45,49,52,55,57};
int k, res = 0;
printf("请输入要查找的数字:\n");
scanf("%d", &k);
res = Fibonacci_Search(a,k,13);
if(res != -1)
printf("在数组的第%d个位置找到元素:%d\n", res + 1, k);
else
printf("未在数组中找到元素:%d\n",k);
return 0;
}
68
1
#include <stdio.h>
2
#include <stdlib.h>
3
#define MAXN 20
4
5
/*
6
*产生斐波那契数列
7
* */
8
void Fibonacci(int *f)
9
{
10
int i;
11
f[0] = 1;
12
f[1] = 1;
13
for(i = 2;i < MAXN; ++i)
14
f[i] = f[i - 2] + f[i - 1];
15
}
16
17
/*
18
* 查找
19
* */
20
int Fibonacci_Search(int *a, int key, int n)
21
{
22
int i, low = 0, high = n - 1;
23
int mid = 0;
24
int k = 0;
25
int F[MAXN];
26
Fibonacci(F);
27
while(n > F[k] - 1) //计算出n在斐波那契中的数列
28
++k;
29
for(i = n;i < F[k] - 1;++i) //把数组补全
30
a[i] = a[high];
31
while(low <= high)
32
{
33
mid = low + F[k-1] - 1; //根据斐波那契数列进行黄金分割
34
if(a[mid] > key)
35
{
36
high = mid - 1;
37
k = k - 1;
38
}
39
else if(a[mid] < key)
40
{
41
low = mid + 1;
42
k = k - 2;
43
}
44
else
45
{
46
if(mid <= high) //如果为真则找到相应的位置
47
return mid;
48
else
49
return -1;
50
}
51
}
52
return 0;
53
}
54
55
int main()
56
{
57
int a[MAXN] = {5,15,19,20,25,31,38,41,45,49,52,55,57};
58
int k, res = 0;
59
printf("请输入要查找的数字:\n");
60
scanf("%d", &k);
61
res = Fibonacci_Search(a,k,13);
62
if(res != -1)
63
printf("在数组的第%d个位置找到元素:%d\n", res + 1, k);
64
else
65
printf("未在数组中找到元素:%d\n",k);
66
return 0;
67
}
68
3.二叉排序树
//****************************BiSortTree.h*************************
#ifndef BISORTTREE_H
#define BISORTTREE_H
#include <stdio.h>
#include <stdlib.h>
#include <stdbool.h>
typedef int datatype;
typedef struct BiSNode
{
datatype data;
struct BiSNode *left,*right;
}BiSNode,*BiSTree;
//在二叉排序树中查找key
bool SearchBST(BiSTree T,datatype key,BiSTree f,BiSTree *p);
//按顺插入
bool InsertBST(BiSTree *T,datatype key);
//删除节点
bool DeleteBST(BiSTree *T,datatype key);
bool Delete(BiSTree *p);
#endif //BISORTTREE_H
//****************************BiSortTree.c*************************
#include "BiSortTree.h"
//在二叉排序树中查找key
bool SearchBST(BiSTree T,datatype key,BiSTree f,BiSTree *p)
{
if(!T)
{
*p = f;
return false;
}
else if(key == T->data)
{
*p = T;
return true;
}
else if(key < T->data)
{
return SearchBST(T->left,key,T,p);
}
else
{
return SearchBST(T->right,key,T,p);
}
}
//按顺插入
bool InsertBST(BiSTree *T,datatype key)
{
BiSTree p,s;
if(!SearchBST(*T,key,NULL,&p))
{
s = (BiSTree)malloc(sizeof(BiSNode));
s->data = key;
s->left = s->right = NULL;
if(!p)
{
*T = s;
}
else if(key < p->data)
{
p->left = s;
}
else
{
p->right = s;
}
return true;
}
else
{
return false;
}
}
//删除节点
bool DeleteBST(BiSTree *T,datatype key)
{
if(!*T)
{
return false;
}
else
{
if(key == (*T)->data)
{
return Delete(T);
}
else if(key < (*T)->data)
{
DeleteBST(&(*T)->left,key);
}
else
{
DeleteBST(&(*T)->right,key);
}
}
}
bool Delete(BiSTree *p)
{
BiSTree q,s;
if(NULL == (*p)->left)
{
q = *p;
*p = (*p)->right;
free(q);
}
else if(NULL == (*p)->right)
{
q = *p;
*p = (*p)->left;
free(q);
}
else
{
q = *p;
s = (*p)->left;
while(s->right)
{
q = s;
s = s->right;
}
(*p)->data = s->data;
if(q != *p)
{
q->right = s->left;
}
else
{
q->left = s->left;
}
free(s);
}
return true;
}
//****************************BiSortTreeTest.c*************************
#include "BiSortTree.h"
int main()
{
int i;
int a[10] ={62,88,58,47,35,73,51,99,37,93};
BiSTree T = NULL;
for(i = 0;i < 10;i++)
{
InsertBST(&T,a[i]);
}
BiSTree p,f;
printf("%d \n",p->data);
SearchBST(T,58,f,&p);
printf("%d \n",p->data);
DeleteBST(&T,58);
printf("%d \n",p->data);
}x
1
//****************************BiSortTree.h*************************
2
#ifndef BISORTTREE_H
3
#define BISORTTREE_H
4
5
6
#include <stdio.h>
7
#include <stdlib.h>
8
#include <stdbool.h>
9
10
typedef int datatype;
11
12
typedef struct BiSNode
13
{
14
datatype data;
15
struct BiSNode *left,*right;
16
}BiSNode,*BiSTree;
17
18
19
//在二叉排序树中查找key
20
bool SearchBST(BiSTree T,datatype key,BiSTree f,BiSTree *p);
21
22
//按顺插入
23
bool InsertBST(BiSTree *T,datatype key);
24
25
//删除节点
26
bool DeleteBST(BiSTree *T,datatype key);
27
28
29
bool Delete(BiSTree *p);
30
31
32
#endif //BISORTTREE_H
33
34
35
//****************************BiSortTree.c*************************
36
#include "BiSortTree.h"
37
38
//在二叉排序树中查找key
39
bool SearchBST(BiSTree T,datatype key,BiSTree f,BiSTree *p)
40
{
41
if(!T)
42
{
43
*p = f;
44
return false;
45
}
46
else if(key == T->data)
47
{
48
*p = T;
49
return true;
50
}
51
else if(key < T->data)
52
{
53
return SearchBST(T->left,key,T,p);
54
}
55
else
56
{
57
return SearchBST(T->right,key,T,p);
58
}
59
}
60
61
//按顺插入
62
bool InsertBST(BiSTree *T,datatype key)
63
{
64
BiSTree p,s;
65
if(!SearchBST(*T,key,NULL,&p))
66
{
67
s = (BiSTree)malloc(sizeof(BiSNode));
68
s->data = key;
69
s->left = s->right = NULL;
70
71
if(!p)
72
{
73
*T = s;
74
}
75
else if(key < p->data)
76
{
77
p->left = s;
78
}
79
else
80
{
81
p->right = s;
82
}
83
return true;
84
}
85
else
86
{
87
return false;
88
}
89
}
90
91
//删除节点
92
bool DeleteBST(BiSTree *T,datatype key)
93
{
94
if(!*T)
95
{
96
return false;
97
}
98
else
99
{
100
if(key == (*T)->data)
101
{
102
return Delete(T);
103
}
104
else if(key < (*T)->data)
105
{
106
DeleteBST(&(*T)->left,key);
107
}
108
else
109
{
110
DeleteBST(&(*T)->right,key);
111
}
112
}
113
}
114
115
bool Delete(BiSTree *p)
116
{
117
BiSTree q,s;
118
119
if(NULL == (*p)->left)
120
{
121
q = *p;
122
*p = (*p)->right;
123
free(q);
124
}
125
else if(NULL == (*p)->right)
126
{
127
q = *p;
128
*p = (*p)->left;
129
free(q);
130
}
131
else
132
{
133
q = *p;
134
s = (*p)->left;
135
136
while(s->right)
137
{
138
q = s;
139
s = s->right;
140
}
141
(*p)->data = s->data;
142
143
if(q != *p)
144
{
145
q->right = s->left;
146
}
147
else
148
{
149
q->left = s->left;
150
}
151
free(s);
152
}
153
return true;
154
}
155
156
//****************************BiSortTreeTest.c*************************
157
#include "BiSortTree.h"
158
159
160
161
int main()
162
{
163
int i;
164
int a[10] ={62,88,58,47,35,73,51,99,37,93};
165
BiSTree T = NULL;
166
for(i = 0;i < 10;i++)
167
{
168
InsertBST(&T,a[i]);
169
}
170
171
BiSTree p,f;
172
printf("%d \n",p->data);
173
SearchBST(T,58,f,&p);
174
printf("%d \n",p->data);
175
176
DeleteBST(&T,58);
177
178
printf("%d \n",p->data);
179
}
4.AVL（平衡二叉树）
#include<stdio.h>
#include<stdlib.h>
#include<stdbool.h>
#define EH 0 /*等高*/
#define LH 1 /*左高*/
#define RH -1 /*右高*/
typedef int ElemType; /*数据类型*/
typedef struct BiTree{
ElemType data; /*数据元素*/
int BF; /*平衡因子*/
struct BiTree *lchild,*rchild; /*左右子女指针*/
}*Bitree,BitreeNode;
int InsertAVL(Bitree *T,ElemType e,bool *taller);
void LeftBalance(Bitree *T);
void RightBalance(Bitree *T);
void R_Rotate(Bitree *T);
void L_Rotate(Bitree *T);
bool *taller;
//bool *taller= (bool *)malloc(sizeof(bool));
int main(void)
{
taller= (bool *)malloc(sizeof(bool));
int data;
Bitree T=NULL;
while(1)
{
printf("enter the number(zero to exit):");
scanf("%d",&data);
if(0==data)break;
InsertAVL(&T,data,taller);
}
return 0;
}
/*若在平衡的二叉排序树T 中不存在和e 有相同关键码的结点，则插入一个数据元素为e 的*/
/*新结点，并反回1，否则反回0。若因插入而使二叉排序树失去平衡，则作平衡旋转处理，*/
/*布尔型变量taller 反映T 长高与否*/
int InsertAVL(Bitree *T,ElemType e,bool *taller)
{
if(!*T) /*插入新结点，树“长高”，置taller 为TURE*/
{
(*T)=(Bitree)malloc(sizeof(BitreeNode));
(*T)->data = e;
(*T)->lchild = (*T)->rchild = NULL;
(*T)->BF = EH;
*taller = true;
}
else
{
if(e==(*T)->data) /*树中存在和e 有相同关键码的结点，不插入*/
{
*taller = false;
return 0;
}
if(e<(*T)->data)
{
if(!InsertAVL(&(*T)->lchild,e,taller)) return 0; /*未插入*/
if(*taller)
switch((*T)->BF)
{
case EH : /*原本左、右子树等高，因左子树增高使树增高*/
(*T)->BF=LH;
*taller=true;
break;
case LH : /*原本左子树高，需作左平衡处理*/
LeftBalance(T);
*taller=false;
break;
case RH : /*原本右子树高，使左、右子树等高*/
(*T)->BF=EH;
*taller=false;
break;
}
}
else
{
if(!InsertAVL(&(*T)->rchild,e,taller)) return 0; /*未插入*/
if(*taller)
switch((*T)->BF)
{
case EH : /*原本左、右子树等高，因右子树增高使树增高*/
(*T)->BF=RH;
*taller=true;
break;
case LH : /*原本左子树高，使左、右子树等高*/
(*T)->BF=EH;
*taller=false;
break;
case RH : /*原本右子树高，需作右平衡处理*/
RightBalance(T);
*taller=false;
break;
}
}
}
return 1;
}
/*对以*p 指向的结点为根的子树，作左平衡旋转处理，处理之后，*p 指向的结点为子树的新根*/
void LeftBalance(Bitree *T)
{
Bitree L=(*T)->lchild,Lr; /*L 指向*T左子树根结点*/
switch(L->BF) /*检查L 平衡度，并作相应处理*/
{
case LH: /*新结点插在*p 左子树的左子树上，需作单右旋转处理*/
(*T)->BF=L->BF=EH;
R_Rotate(T);
break;
case EH: /*原本左、右子树等高，因左子树增高使树增高*/
(*T)->BF=LH; //这里的EH好像没有写的必要
*taller=true;
break;
case RH: /*新结点插在*T 左孩子的右子树上，需作先左后右双旋处理*/
Lr=L->rchild; /*Lr 指向*p 左孩子的右子树根结点*/
switch(Lr->BF) /*修正*T 及其左子树的平衡因子*/
{
case LH:
(*T)->BF = RH;
L->BF = EH;
break;
case EH:
(*T)->BF = L->BF= EH;
break;
case RH:
(*T)->BF = EH;
L->BF = LH;
break;
}
Lr->BF = EH;
L_Rotate(&L); /*对*T 的左子树作左旋转处理*/
R_Rotate(T); /*对*T 作右旋转处理*/
}
}
//这里和leftbalance一个道理，试着自己写一下
void RightBalance(Bitree *T)
{
Bitree Lr= (*T)->rchild,L;
switch(Lr->BF)
{
case EH:
*taller = true;
(*T)->BF = RH;
break;
case RH:
(*T)->BF=Lr->BF=EH;
L_Rotate(T);
break;
case LH:
L = Lr->lchild;
switch(L->BF)
{
case EH:
(*T)->BF=Lr->BF= EH;
break;
case RH:
Lr->BF= EH;
(*T)->BF = LH;
break;
case LH:
(*T)->BF = LH;
Lr->BF = EH;
break;
}
L->BF = EH;
R_Rotate(&Lr);
L_Rotate(T);
}
}
/*对以*T 指向的结点为根的子树，作右单旋转处理，处理之后，*T 指向的结点为子树的新根*/
void R_Rotate(Bitree *T)
{
Bitree L=(*T)->lchild; /*L 指向*T 左子树根结点*/
(*T)->lchild=L->rchild; /*L 的右子树挂接*T 的左子树*/
L->rchild=*T; *T=L; /* *L 指向新的根结点*/
}
/*对以*p 指向的结点为根的子树，作左单旋转处理，处理之后，*p 指向的结点为子树的新根*/
void L_Rotate(Bitree *T)
{
Bitree Lr=(*T)->rchild; /*Lr 指向*T 右子树根结点*/
(*T)->rchild=Lr->lchild; /*L 的左子树挂接*p 的右子树*/
Lr->lchild=*T;
*T=Lr; /* *L 指向新的根结点*/
}1
209
1
#include<stdio.h>
2
#include<stdlib.h>
3
#include<stdbool.h>
4
#define EH 0 /*等高*/
5
#define LH 1 /*左高*/
6
#define RH -1 /*右高*/
7
8
typedef int ElemType; /*数据类型*/
9
10
typedef struct BiTree{
11
ElemType data; /*数据元素*/
12
int BF; /*平衡因子*/
13
struct BiTree *lchild,*rchild; /*左右子女指针*/
14
}*Bitree,BitreeNode;
15
16
17
int InsertAVL(Bitree *T,ElemType e,bool *taller);
18
void LeftBalance(Bitree *T);
19
void RightBalance(Bitree *T);
20
void R_Rotate(Bitree *T);
21
void L_Rotate(Bitree *T);
22
bool *taller;
23
//bool *taller= (bool *)malloc(sizeof(bool));
24
25
int main(void)
26
{
27
taller= (bool *)malloc(sizeof(bool));
28
int data;
29
Bitree T=NULL;
30
while(1)
31
{
32
printf("enter the number(zero to exit):");
33
scanf("%d",&data);
34
if(0==data)break;
35
InsertAVL(&T,data,taller);
36
37
}
38
39
40
41
return 0;
42
}
43
44
45
/*若在平衡的二叉排序树T 中不存在和e 有相同关键码的结点，则插入一个数据元素为e 的*/
46
/*新结点，并反回1，否则反回0。若因插入而使二叉排序树失去平衡，则作平衡旋转处理，*/
47
/*布尔型变量taller 反映T 长高与否*/
48
int InsertAVL(Bitree *T,ElemType e,bool *taller)
49
{
50
if(!*T) /*插入新结点，树“长高”，置taller 为TURE*/
51
{
52
(*T)=(Bitree)malloc(sizeof(BitreeNode));
53
(*T)->data = e;
54
(*T)->lchild = (*T)->rchild = NULL;
55
(*T)->BF = EH;
56
*taller = true;
57
}
58
else
59
{
60
if(e==(*T)->data) /*树中存在和e 有相同关键码的结点，不插入*/
61
{
62
*taller = false;
63
return 0;
64
}
65
if(e<(*T)->data)
66
{
67
if(!InsertAVL(&(*T)->lchild,e,taller)) return 0; /*未插入*/
68
if(*taller)
69
switch((*T)->BF)
70
{
71
case EH : /*原本左、右子树等高，因左子树增高使树增高*/
72
(*T)->BF=LH;
73
*taller=true;
74
break;
75
76
case LH : /*原本左子树高，需作左平衡处理*/
77
LeftBalance(T);
78
*taller=false;
79
break;
80
81
case RH : /*原本右子树高，使左、右子树等高*/
82
(*T)->BF=EH;
83
*taller=false;
84
break;
85
86
}
87
88
}
89
else
90
{
91
if(!InsertAVL(&(*T)->rchild,e,taller)) return 0; /*未插入*/
92
if(*taller)
93
switch((*T)->BF)
94
{
95
case EH : /*原本左、右子树等高，因右子树增高使树增高*/
96
(*T)->BF=RH;
97
*taller=true;
98
break;
99
100
case LH : /*原本左子树高，使左、右子树等高*/
101
(*T)->BF=EH;
102
*taller=false;
103
break;
104
105
case RH : /*原本右子树高，需作右平衡处理*/
106
RightBalance(T);
107
*taller=false;
108
break;
109
110
}
111
}
112
}
113
return 1;
114
}
115
116
117
118
/*对以*p 指向的结点为根的子树，作左平衡旋转处理，处理之后，*p 指向的结点为子树的新根*/
119
void LeftBalance(Bitree *T)
120
{
121
Bitree L=(*T)->lchild,Lr; /*L 指向*T左子树根结点*/
122
switch(L->BF) /*检查L 平衡度，并作相应处理*/
123
{
124
case LH: /*新结点插在*p 左子树的左子树上，需作单右旋转处理*/
125
(*T)->BF=L->BF=EH;
126
R_Rotate(T);
127
break;
128
case EH: /*原本左、右子树等高，因左子树增高使树增高*/
129
(*T)->BF=LH; //这里的EH好像没有写的必要
130
*taller=true;
131
break;
132
case RH: /*新结点插在*T 左孩子的右子树上，需作先左后右双旋处理*/
133
Lr=L->rchild; /*Lr 指向*p 左孩子的右子树根结点*/
134
switch(Lr->BF) /*修正*T 及其左子树的平衡因子*/
135
{
136
case LH:
137
(*T)->BF = RH;
138
L->BF = EH;
139
break;
140
case EH:
141
(*T)->BF = L->BF= EH;
142
break;
143
case RH:
144
(*T)->BF = EH;
145
L->BF = LH;
146
break;
147
148
}
149
Lr->BF = EH;
150
L_Rotate(&L); /*对*T 的左子树作左旋转处理*/
151
R_Rotate(T); /*对*T 作右旋转处理*/
152
}
153
}
154
//这里和leftbalance一个道理，试着自己写一下
155
void RightBalance(Bitree *T)
156
{
157
Bitree Lr= (*T)->rchild,L;
158
switch(Lr->BF)
159
{
160
case EH:
161
*taller = true;
162
(*T)->BF = RH;
163
break;
164
case RH:
165
(*T)->BF=Lr->BF=EH;
166
L_Rotate(T);
167
break;
168
case LH:
169
L = Lr->lchild;
170
switch(L->BF)
171
{
172
case EH:
173
(*T)->BF=Lr->BF= EH;
174
break;
175
case RH:
176
Lr->BF= EH;
177
(*T)->BF = LH;
178
break;
179
case LH:
180
(*T)->BF = LH;
181
Lr->BF = EH;
182
break;
183
184
}
185
L->BF = EH;
186
R_Rotate(&Lr);
187
L_Rotate(T);
188
189
}
190
}
191
192
193
/*对以*T 指向的结点为根的子树，作右单旋转处理，处理之后，*T 指向的结点为子树的新根*/
194
void R_Rotate(Bitree *T)
195
{
196
Bitree L=(*T)->lchild; /*L 指向*T 左子树根结点*/
197
(*T)->lchild=L->rchild; /*L 的右子树挂接*T 的左子树*/
198
L->rchild=*T; *T=L; /* *L 指向新的根结点*/
199
}
200
201
202
/*对以*p 指向的结点为根的子树，作左单旋转处理，处理之后，*p 指向的结点为子树的新根*/
203
void L_Rotate(Bitree *T)
204
{
205
Bitree Lr=(*T)->rchild; /*Lr 指向*T 右子树根结点*/
206
(*T)->rchild=Lr->lchild; /*L 的左子树挂接*p 的右子树*/
207
Lr->lchild=*T;
208
*T=Lr; /* *L 指向新的根结点*/
209
}
附件列表
Chapter 8(查找)的更多相关文章
- Chapter 5 查找
Chapter 5 查找 1- 顺序查找法 O(n) 2- 折半查找O(logn) :二分查找 要求:关键字有序 过程: 判定树:叶子结点为方框,代表不成功的结点. 3- 分块查找:索引顺 ...
- 【ASP.NET Identity系列教程（一）】ASP.NET Identity入门
注:本文是[ASP.NET Identity系列教程]的第一篇.本系列教程详细.完整.深入地介绍了微软的ASP.NET Identity技术,描述了如何运用ASP.NET Identity实现应用程序 ...
- ASP.NET Identity 一 （转载）
来源:http://www.cnblogs.com/r01cn/p/5194257.html 注:本文是[ASP.NET Identity系列教程]的第一篇.本系列教程详细.完整.深入地介绍了微软的A ...
- ASP.NET Identity系列教程-2【Identity入门】
https://www.cnblogs.com/r01cn/p/5177708.html13 Identity入门 Identity is a new API from Microsoft to ma ...
- Chapter 3: Connector(连接器)
一.概述 Tomcat或者称之为Catalina(开发名称),可以简化为两个主要的模块,如下图: 多个Connector关联一个Container.之所以需要多个Connector,是为了处理多种协议 ...
- Chapter Schema
Chapter Schema Schema是XF的核心,每一个读写方法都有一个相关联的Schema.方法首先解析Schema,然后再根据Schema的配置的执行. 那Schema是什么呢?Schema ...
- Chapter 1 Securing Your Server and Network(9):使用Kerberos用于身份验证
原文:Chapter 1 Securing Your Server and Network(9):使用Kerberos用于身份验证 原文出处:http://blog.csdn.net/dba_huan ...
- Linux - 在当前系统内查找信息的方法
查找文本 使用grep命令 grep命令 - 示例 grep命令 - 正则表达式 grep命令 - 统计匹配字符串的行数 grep命令 - 搜索多个单词 结合正则表达式使用grep命令 注意:在搜索指 ...
- 《Linux内核设计与实现》Chapter 18 读书笔记
<Linux内核设计与实现>Chapter 18 读书笔记 一.准备开始 一个bug 一个藏匿bug的内核版本 知道这个bug最早出现在哪个内核版本中. 相关内核代码的知识和运气 想要成功 ...
随机推荐
- route命令详情
基础命令学习目录首页 原文链接:https://www.cnblogs.com/lpfuture/p/5857738.html 考试题一:linux下如何添加路由(百度面试题) 以上是原题,老男孩老师 ...
- MegaCli64/MegaCli命令详解
基础命令学习目录首页 MegaCli64 -LDInfo -Lall -aALL这个命令能看到RAID的状态MegaCli64 -LDSetProp ForcedWB -L0 -a0MegaCli64 ...
- Ubuntu 1804 本地显示远程服务器文件
本地是 Ubuntu 1804 最近想查看服务器上的图片,之前都是scp到本地,感觉太麻烦,于是查到有一种方法,ssh图形界面那种: 1.在File 界面下,左侧文件栏的最后一列有 “+ Other ...
- python处理xml实例
""" Author = zyh FileName = read_xml_1.py Time = 18-9-26 下午5:19 """ fr ...
- Android笔记-4-实现登陆页面并跳转和简单的注册页面
实现登陆页面并跳转和简单的注册页面 首先我们来看看布局的xml代码 login.xml <span style="font-family:Arial;font-size:18px; ...
- windows和RedHat双系统安装说明
该博客记录了安装windows和RedHat双系统的方法.这里的windows系统是win8.1,RedHat是RHEL-server-7.0-x86_64-LinuxProbe.Com.iso,该i ...
- java中的互斥锁和信号量的区别
互斥锁和信号量都是操作系统中为并发编程设计基本概念,互斥锁和信号量的概念上的不同在于,对于同一个资源,互斥锁只有0和1 的概念,而信号量不止于此.也就是说,信号量可以使资源同时被多个线程访问,而互斥锁 ...
- grunt入门讲解2：如何使用 Gruntfile 配置任务
Grunt的task配置都是在 Gruntfile 中的grunt.initConfig方法中指定的.此配置主要包括以任务名称命名的属性,和其他任意数据.一旦这些代表任意数据的属性与任务所需要的属性相 ...
- Prism框架的优点
以我粗略的了解,prism/mvvm可以做到完全的逻辑和ui分离.即便是事件都是如此.这是主要优点.mvc是从本质上ui框架(当前大量半吊子把业务逻辑写在里面是不对的),mvvm包含客户端的业务逻辑. ...
- appium启动sdk的android模拟器
(1)启动sdk安装目录下的AVD Manager.exe (2)如下图,点击[create]按钮 (3)如下图,设置虚拟机的配置,至于Target中的:Android 4.4.2是在安装sdk的时候 ...