KMP的原理详细讲解

1.kmp算法的原理：

　　本部分内容转自：http://www.cnblogs.com/c-cloud/p/3224788.html及                           http://www.ruanyifeng.com/blog/2013/05/Knuth%E2%80%93Morris%E2%80%93Pratt_algorithm.html

字符串匹配是计算机的基本任务之一。

举例来说，有一个字符串"BBC ABCDAB ABCDABCDABDE"，我想知道，里面是否包含另一个字符串"ABCDABD"？

许多算法可以完成这个任务，Knuth-Morris-Pratt算法（简称KMP）是最常用的之一。它以三个发明者命名，起头的那个K就是著名科学家Donald Knuth。

这种算法不太容易理解，网上有很多解释，但读起来都很费劲。直到读到Jake Boxer的文章，我才真正理解这种算法。下面，我用自己的语言，试图写一篇比较好懂的KMP算法解释。

1.

首先，字符串"BBC ABCDAB ABCDABCDABDE"的第一个字符与搜索词"ABCDABD"的第一个字符，进行比较。因为B与A不匹配，所以搜索词后移一位。

2.

因为B与A不匹配，搜索词再往后移。

3.

就这样，直到字符串有一个字符，与搜索词的第一个字符相同为止。

4.

接着比较字符串和搜索词的下一个字符，还是相同。

5.

直到字符串有一个字符，与搜索词对应的字符不相同为止。

6.

这时，最自然的反应是，将搜索词整个后移一位，再从头逐个比较。这样做虽然可行，但是效率很差，因为你要把"搜索位置"移到已经比较过的位置，重比一遍。

7.

一个基本事实是，当空格与D不匹配时，你其实知道前面六个字符是"ABCDAB"。KMP算法的想法是，设法利用这个已知信息，不要把"搜索位置"移回已经比较过的位置，继续把它向后移，这样就提高了效率。

8.

怎么做到这一点呢？可以针对搜索词，算出一张《部分匹配表》（Partial Match Table）。这张表是如何产生的，后面再介绍，这里只要会用就可以了。

9.

已知空格与D不匹配时，前面六个字符"ABCDAB"是匹配的。查表可知，最后一个匹配字符B对应的"部分匹配值"为2，因此按照下面的公式算出向后移动的位数：

　　移动位数 = 已匹配的字符数 - 对应的部分匹配值

因为 6 - 2 等于4，所以将搜索词向后移动4位。

10.

因为空格与Ｃ不匹配，搜索词还要继续往后移。这时，已匹配的字符数为2（"AB"），对应的"部分匹配值"为0。所以，移动位数 = 2 - 0，结果为 2，于是将搜索词向后移2位。

11.

因为空格与A不匹配，继续后移一位。

12.

逐位比较，直到发现C与D不匹配。于是，移动位数 = 6 - 2，继续将搜索词向后移动4位。

13.

逐位比较，直到搜索词的最后一位，发现完全匹配，于是搜索完成。如果还要继续搜索（即找出全部匹配），移动位数 = 7 - 0，再将搜索词向后移动7位，这里就不再重复了。

14.

下面介绍《部分匹配表》是如何产生的。

首先，要了解两个概念："前缀"和"后缀"。 "前缀"指除了最后一个字符以外，一个字符串的全部头部组合；"后缀"指除了第一个字符以外，一个字符串的全部尾部组合。

15.

"部分匹配值"就是"前缀"和"后缀"的最长的共有元素的长度。以"ABCDABD"为例，

　　－　"A"的前缀和后缀都为空集，共有元素的长度为0；

　　－　"AB"的前缀为[A]，后缀为[B]，共有元素的长度为0；

　　－　"ABC"的前缀为[A, AB]，后缀为[BC, C]，共有元素的长度0；

　　－　"ABCD"的前缀为[A, AB, ABC]，后缀为[BCD, CD, D]，共有元素的长度为0；

　　－　"ABCDA"的前缀为[A, AB, ABC, ABCD]，后缀为[BCDA, CDA, DA, A]，共有元素为"A"，长度为1；

　　－　"ABCDAB"的前缀为[A, AB, ABC, ABCD, ABCDA]，后缀为[BCDAB, CDAB, DAB, AB, B]，共有元素为"AB"，长度为2；

　　－　"ABCDABD"的前缀为[A, AB, ABC, ABCD, ABCDA, ABCDAB]，后缀为[BCDABD, CDABD, DABD, ABD, BD, D]，共有元素的长度为0。

16.

"部分匹配"的实质是，有时候，字符串头部和尾部会有重复。比如，"ABCDAB"之中有两个"AB"，那么它的"部分匹配值"就是2（"AB"的长度）。搜索词移动的时候，第一个"AB"向后移动4位（字符串长度-部分匹配值），就可以来到第二个"AB"的位置。

2.next数组的求解思路

　　通过上文完全可以对kmp算法的原理有个清晰的了解，那么下一步就是编程实现了，其中最重要的就是如何根据待匹配的模版字符串求出对应每一位的最大相同前后缀的长度。我先给出我的代码：

 1 void makeNext(const char P[],int next[])
 2 {
 3     int q,k;//q:模版字符串下标；k:最大前后缀长度
 4     int m = strlen(P);//模版字符串长度
 5     next[0] = 0;//模版字符串的第一个字符的最大前后缀长度为0
 6     for (q = 1,k = 0; q < m; ++q)//for循环，从第二个字符开始，依次计算每一个字符对应的next值
 7     {
 8         while(k > 0 && P[q] != P[k])//递归的求出P[0]···P[q]的最大的相同的前后缀长度k
 9             k = next[k-1];          //不理解没关系看下面的分析，这个while循环是整段代码的精髓所在，确实不好理解
10         if (P[q] == P[k])//如果相等，那么最大相同前后缀长度加1
11         {
12             k++;
13         }
14         next[q] = k;
15     }
16 } 

　　现在我着重讲解一下while循环所做的工作：

1. 　　已知前一步计算时最大相同的前后缀长度为k（k>0），即P[0]···P[k-1]；
2. 　　此时比较第k项P[k]与P[q],如图1所示
3. 　　如果P[K]等于P[q]，那么很简单跳出while循环;
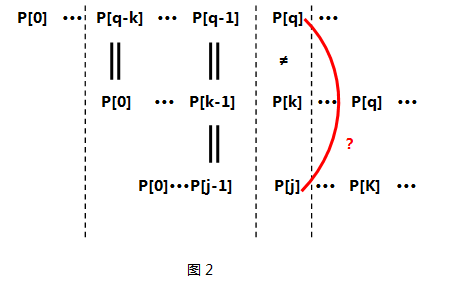
4. 　　关键！关键有木有！关键如果不等呢？？？那么我们应该利用已经得到的next[0]···next[k-1]来求P[0]···P[k-1]这个子串中最大相同前后缀，可能有同学要问了——为什么要求P[0]···P[k-1]的最大相同前后缀呢？？？是啊！为什么呢？ 原因在于P[k]已经和P[q]失配了，而且P[q-k] ··· P[q-1]又与P[0] ···P[k-1]相同，看来P[0]···P[k-1]这么长的子串是用不了了，那么我要找个同样也是P[0]打头、P[k-1]结尾的子串即P[0]···P[j-1](j==next[k-1])，看看它的下一项P[j]是否能和P[q]匹配。如图2所示

附代码：

 1 #include<stdio.h>
 2 #include<string.h>
 3 void makeNext(const char P[],int next[])
 4 {
 5     int q,k;
 6     int m = strlen(P);
 7     next[0] = 0;
 8     for (q = 1,k = 0; q < m; ++q)
 9     {
10         while(k > 0 && P[q] != P[k])
11             k = next[k-1];
12         if (P[q] == P[k])
13         {
14             k++;
15         }
16         next[q] = k;
17     }
18 }
19
20 int kmp(const char T[],const char P[],int next[])
21 {
22     int n,m;
23     int i,q;
24     n = strlen(T);
25     m = strlen(P);
26     makeNext(P,next);
27     for (i = 0,q = 0; i < n; ++i)
28     {
29         while(q > 0 && P[q] != T[i])
30             q = next[q-1];
31         if (P[q] == T[i])
32         {
33             q++;
34         }
35         if (q == m)
36         {
37             printf("Pattern occurs with shift:%d\n",(i-m+1));
38         }
39     }
40 }
41
42 int main()
43 {
44     int i;
45     int next[20]={0};
46     char T[] = "ababxbababcadfdsss";
47     char P[] = "abcdabd";
48     printf("%s\n",T);
49     printf("%s\n",P );
50     // makeNext(P,next);
51     kmp(T,P,next);
52     for (i = 0; i < strlen(P); ++i)
53     {
54         printf("%d ",next[i]);
55     }
56     printf("\n");
57
58     return 0;
59 }

扩展KMP的思想：对于字符串s[],next[i]为以是s[i]开始与s前缀的最大匹配长度；

扩展KMP讲解

刘雅琼PPT讲解链接