Coding the Matrix (0)：映射、复数和域

1. 非常好的 Python 教程

《深入 Python 3.0》 以及 IBM 开发社区的博客探索 Python.

2. 子集: s 是 S 的子集

>>>S = {2, 3, 4, 5, 6, 7}
>>>s = {x for x in S if x%2==0} # 偶数子集
>>>s
set([2, 4, 6])

3. 映射：Ceasar 加密

>>> import string
>>> table = string.maketrans("abcdefghijklmnopqrstuvwxyz", "cdefghijklmnopqrstuvwxyzab") # 向后平移两位
>>> print "hello".translate(table)
jgnnq

4. 复数练习

>>> 1 + 1j
(1+1j)
>>> 1 + 1j + (10 + 20j) # 相加
(11+21j)
>>> x = 1 + 3j
>>> (x - 1)**2 # 相乘
(-9+0j)
>>> x.real # 实部
1.0
>>> x.imag # 虚部
3.0
>>> type(x)
<type 'complex'>

5. 复平面

• 复数的绝对值

  >>> abs(3 + 4j)
  5.0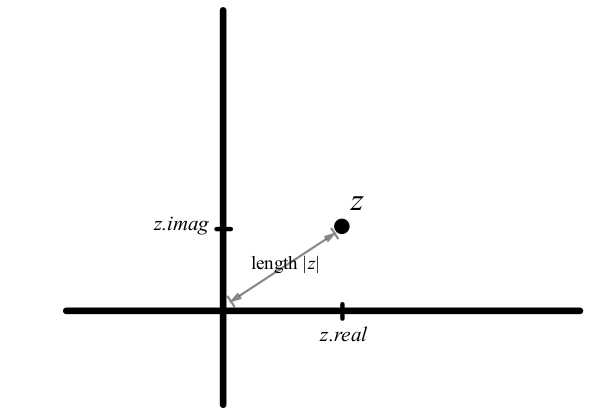

  

• 复数画点

  plotting.py 的下载地址

  >>> from plotting import plot
  >>> L = [2+2j, 3+2j, 1.75+1j, 2+1j, 2.25+1j, 2.5+1j, 2.75+1j, 3+1j, 3.25+1j]
  >>> plot(L)

  画图如下:

  

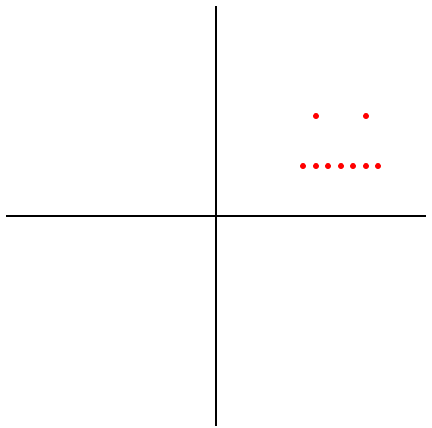
• 复数画图

  >>> from image import *
  >>> I = color2gray(file2image('./pic/01.png'))
  >>> row = len(I) # 垂直高度
  >>> col = len(I[0]) # 水平长度
  >>> M = [x + y*1j for x in range(col) for y in range(row) if I[row-y-1][x] < 120]
  >>> plot(M, max(row, col), 1) # 第二个参数便于坐标系大小的自动调节， 第三个参数表示每个像素显示的大小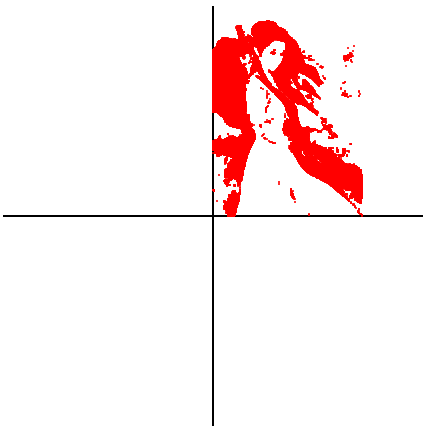

  

• 图像平移

  (x + yi) to (a+x + (b+y)i)

  >>> plot({z + (1+2j) for z in L})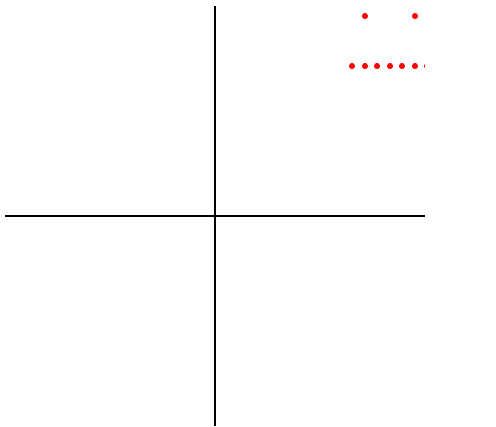

  

• 图像缩放

  (x + yi) to (0.5x + 0.5yi)

  >>> plot([.5*z for z in M], max(row, col), 1)

  

• 中心对称变换

  (x + yi) to (-x - yi)

  >>> plot({-z for z in L})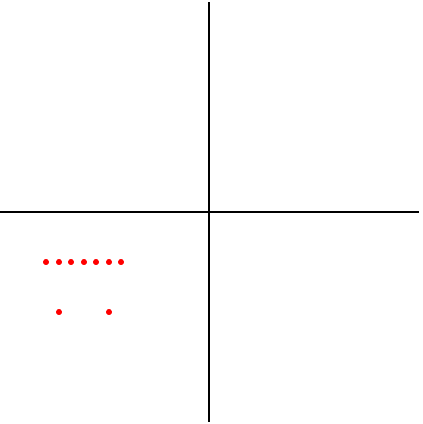

  

• 以坐标轴为中心旋转 90 度

  (x + yi) to (-y + xi)

  the same as:

  (x + yi) to i*(x + yi)

  >>> plot({1j*z for z in L})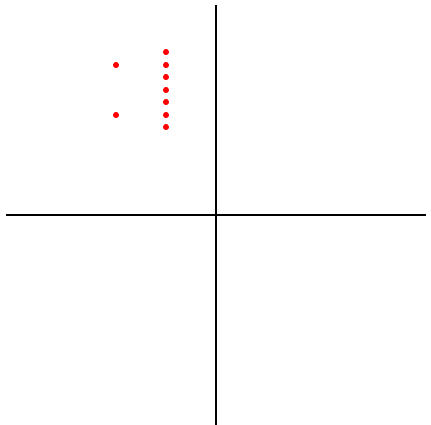

  

• 以坐标轴为中心任意旋转和缩放

  

  旋转 45 度：

  >>> from math import pi, e
  >>> plot([e**(pi*1j/4)*z for z in M], max(row, col), 1)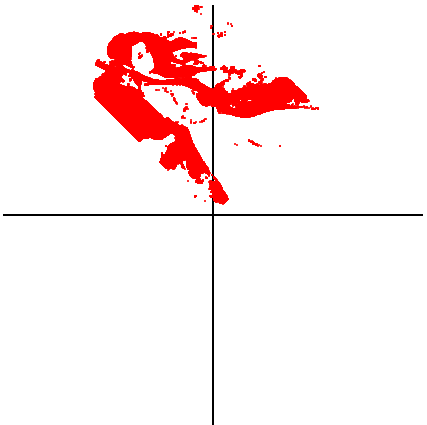

  

  欧拉恒等式：

  欧拉公式：

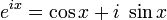
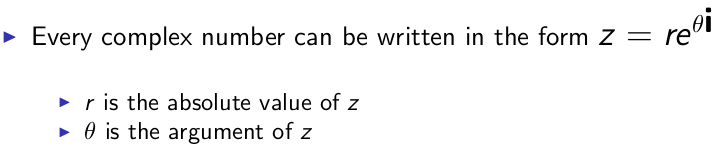
6. Playing with GF(2)

• 玩玩有限域(伽罗华域， galois field)

  galois field 2 只有两个元素： 0 和 1. 在这个域中，加法运算是异或操作，乘法运算是与操作。运算律比如分配律在这里仍然适用。

  >>> from GF2 import one
  >>> one + one
  0
  >>> one + 0
  one
  >>> one * one
  one
  >>> one * 0
  0
  >>> one / one
  one

  对于这样一个加密系统：

  

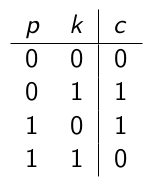
  概率均匀分布，并且密文与明文是独立的。

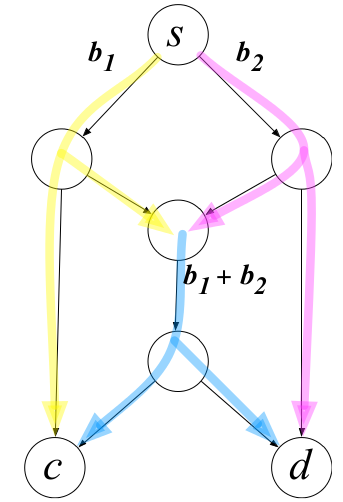
• Network coding

  Streaming video through network

  a) 一个顾客木有问题

  

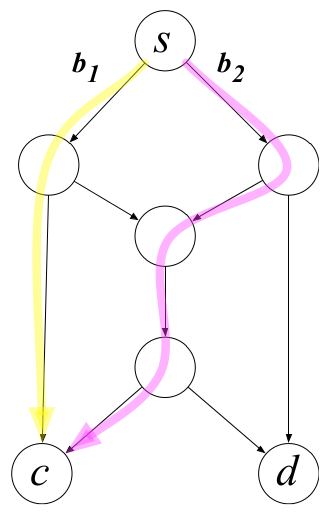
  b) 两个顾客发生冲突

  

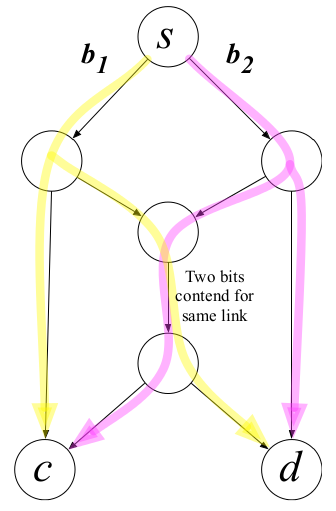
  c) 先编码，再解码，两个发送端可同时发送到两个接收端