BZOJ1018[SHOI2008]堵塞的交通——线段树

题目描述

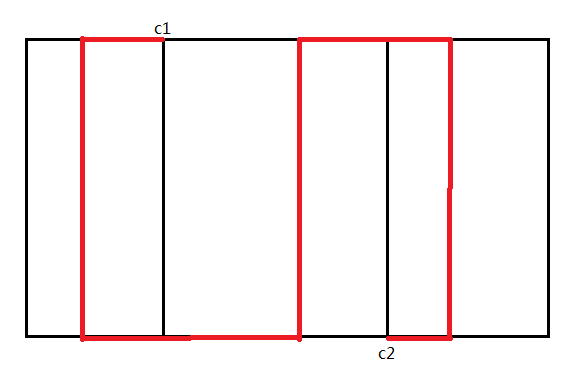
　　有一天，由于某种穿越现象作用，你来到了传说中的小人国。小人国的布局非常奇特，整个国家的交通系统可
以被看成是一个2行C列的矩形网格，网格上的每个点代表一个城市，相邻的城市之间有一条道路，所以总共有2C个
城市和3C-2条道路。 小人国的交通状况非常槽糕。有的时候由于交通堵塞，两座城市之间的道路会变得不连通，
直到拥堵解决，道路才会恢复畅通。初来咋到的你决心毛遂自荐到交通部某份差事，部长听说你来自一个科技高度
发达的世界，喜出望外地要求你编写一个查询应答系统，以挽救已经病入膏肓的小人国交通系统。 小人国的交通
部将提供一些交通信息给你，你的任务是根据当前的交通情况回答查询的问题。交通信息可以分为以下几种格式：
Close r1 c1 r2 c2：相邻的两座城市(r1,c1)和(r2,c2)之间的道路被堵塞了；Open r1 c1 r2 c2：相邻的两座城
市(r1,c1)和(r2,c2)之间的道路被疏通了；Ask r1 c1 r2 c2：询问城市(r1,c1)和(r2,c2)是否连通。如果存在一
条路径使得这两条城市连通，则返回Y，否则返回N；

输入

　　第一行只有一个整数C，表示网格的列数。接下来若干行，每行为一条交通信息，以单独的一行“Exit”作为
结束。我们假设在一开始所有的道路都是堵塞的。我们保证 C小于等于100000，信息条数小于等于100000。

输出

　　对于每个查询，输出一个“Y”或“N”。

样例输入

2
Open 1 1 1 2
Open 1 2 2 2
Ask 1 1 2 2
Ask 2 1 2 2
Exit

样例输出

Y
N

 

线段树维护连通性经典题。

怎么用线段树维护连通性？

因为只有两行，那么我们对列来建线段树，每一列分为上端点和下端点。

对于线段树的一个点维护这个点所代表区间的左上端点(lu)、右上端点(ru)、左下端点(ld)、右下端点(rd)这四个点之间的连通性。

回溯时直接合并左右子树代表的区间的信息。

同时还要记录对于一列x与x+1列之间的连通性，这个在回溯合并时会用到。

修改分为两种：修改横边和修改竖边。

修改竖边直接递归找修改边对应的那一列，然后回溯更新沿途信息。

修改横边递归找到当前区间的mid等于横边左端点所在列x，修改x与x+1列之间的连通性再回溯更新沿途信息。

查询时将查询到的log个区间合并，然后判断查询点的连通性？

考虑这样一种特殊情况：

显然只查中间区间之后判断是不连通的，因此还要查[1,c1]和[c2,c]这两端的区间然后分情况讨论。

具体实现见代码，其中lu,ld,ru,rd为上述的区间四个端点。

#include<set>
#include<map>
#include<stack>
#include<queue>
#include<cmath>
#include<cstdio>
#include<vector>
#include<bitset>
#include<cstring>
#include<iostream>
#include<algorithm>
#define ll long long
using namespace std;
int t[100010][8];
int n;
char ch[10];
int a,b,c,d;
struct miku
{
    int luld;
    int rurd;
    int lurd;
    int ruld;
    int luru;
    int ldrd;
}s[800010];
void merge(miku &z,miku x,miku y,int mid)
{
    z.luld=(x.luld)||(x.luru&&t[mid][1]&&y.luld&&t[mid][2]&&x.ldrd);
    z.rurd=(y.rurd)||(y.luru&&t[mid][1]&&x.rurd&&t[mid][2]&&y.ldrd);
    z.lurd=(x.lurd&&t[mid][2]&&y.ldrd)||(x.luru&&t[mid][1]&&y.lurd);
    z.ruld=(x.ruld&&t[mid][1]&&y.luru)||(x.ldrd&&t[mid][2]&&y.ruld);
    z.luru=(x.lurd&&t[mid][2]&&y.ruld)||(x.luru&&t[mid][1]&&y.luru);
    z.ldrd=(x.ruld&&t[mid][1]&&y.lurd)||(x.ldrd&&t[mid][2]&&y.ldrd);
}
void build(int rt,int l,int r)
{
    if(l==r)
    {
        s[rt].luru=1;
        s[rt].ldrd=1;
        return ;
    }
    int mid=(l+r)>>1;
    build(rt<<1,l,mid);
    build(rt<<1|1,mid+1,r);
    merge(s[rt],s[rt<<1],s[rt<<1|1],mid);
}
void change1(int rt,int l,int r,int x,int k)
{
    if(l==r)
    {
        s[rt].lurd=s[rt].ruld=s[rt].luld=s[rt].rurd=k;
        return ;
    }
    int mid=(l+r)>>1;
    if(x<=mid)
    {
        change1(rt<<1,l,mid,x,k);
    }
    else if(x>mid)
    {
        change1(rt<<1|1,mid+1,r,x,k);
    }
    merge(s[rt],s[rt<<1],s[rt<<1|1],mid);
}
void change2(int rt,int l,int r,int x,int y,int k)
{
    int mid=(l+r)>>1;
    if(x==mid)
    {
        t[x][y]=k;
        merge(s[rt],s[rt<<1],s[rt<<1|1],mid);
        return ;
    }
    if(x<=mid)
    {
        change2(rt<<1,l,mid,x,y,k);
    }
    else if(x>mid)
    {
        change2(rt<<1|1,mid+1,r,x,y,k);
    }
    merge(s[rt],s[rt<<1],s[rt<<1|1],mid);
}
miku query(int rt,int l,int r,int L,int R)
{
    if(L<=l&&r<=R)
    {
        return s[rt];
    }
    int mid=(l+r)>>1;
    if(R<=mid)
    {
        return query(rt<<1,l,mid,L,R);
    }
    if(L>mid)
    {
        return query(rt<<1|1,mid+1,r,L,R);
    }
    miku ans;
    merge(ans,query(rt<<1,l,mid,L,R),query(rt<<1|1,mid+1,r,L,R),mid);
    return ans;
}
int ask(int a,int b,int c,int d)
{
    miku ls=query(1,1,n,1,b);
    miku ms=query(1,1,n,b,d);
    miku rs=query(1,1,n,d,n);
    int t1,t2,t3,t4;
    if(a==1&&c==1)
    {
        t1=ms.luru;
        t2=(ls.rurd&&ms.ruld);
        t3=(ms.lurd&&rs.luld);
        t4=(ls.rurd&&ms.ldrd&&rs.luld);
        if(t1||t2||t3||t4)
        {
            return 1;
        }
        else
        {
            return 0;
        }
    }
    else if(a==1&&c==2)
    {
        t1=ms.lurd;
        t2=(ls.rurd&&ms.ldrd);
        t3=(ms.luru&&rs.luld);
        t4=(ls.rurd&&ms.ruld&&rs.luld);
        if(t1||t2||t3||t4)
        {
            return 1;
        }
        else
        {
            return 0;
        }
    }
    else if(a==2&&c==1)
    {
        t1=ms.ruld;
        t2=(ls.rurd&&ms.luru);
        t3=(ms.ldrd&&rs.luld);
        t4=(ls.rurd&&ms.lurd&&rs.luld);
        if(t1||t2||t3||t4)
        {
            return 1;
        }
        else
        {
            return 0;
        }
    }
    else if(a==2&&c==2)
    {
        t1=ms.ldrd;
        t2=(ls.rurd&&ms.lurd);
        t3=(ms.ruld&&rs.luld);
        t4=(ls.rurd&&ms.luru&&rs.luld);
        if(t1||t2||t3||t4)
        {
            return 1;
        }
        else
        {
            return 0;
        }
    }
}
int main()
{
    scanf("%d",&n);
    build(1,1,n);
    while(1)
    {
        scanf("%s",ch);
        if(ch[0]=='E')
        {
            break;
        }
        scanf("%d%d%d%d",&a,&b,&c,&d);
        if(b>d)
        {
            swap(b,d);
            swap(a,c);
        }
        if(ch[0]=='O')
        {
            if(a==c)
            {
                change2(1,1,n,b,a,1);
            }
            else
            {
                change1(1,1,n,b,1);
            }
        }
        else if(ch[0]=='C')
        {
            if(a==c)
            {
                change2(1,1,n,b,a,0);
            }
            else
            {
                change1(1,1,n,b,0);
            }
        }
        else
        {
            ask(a,b,c,d)==1?printf("Y\n"):printf("N\n");
        }
    }
}