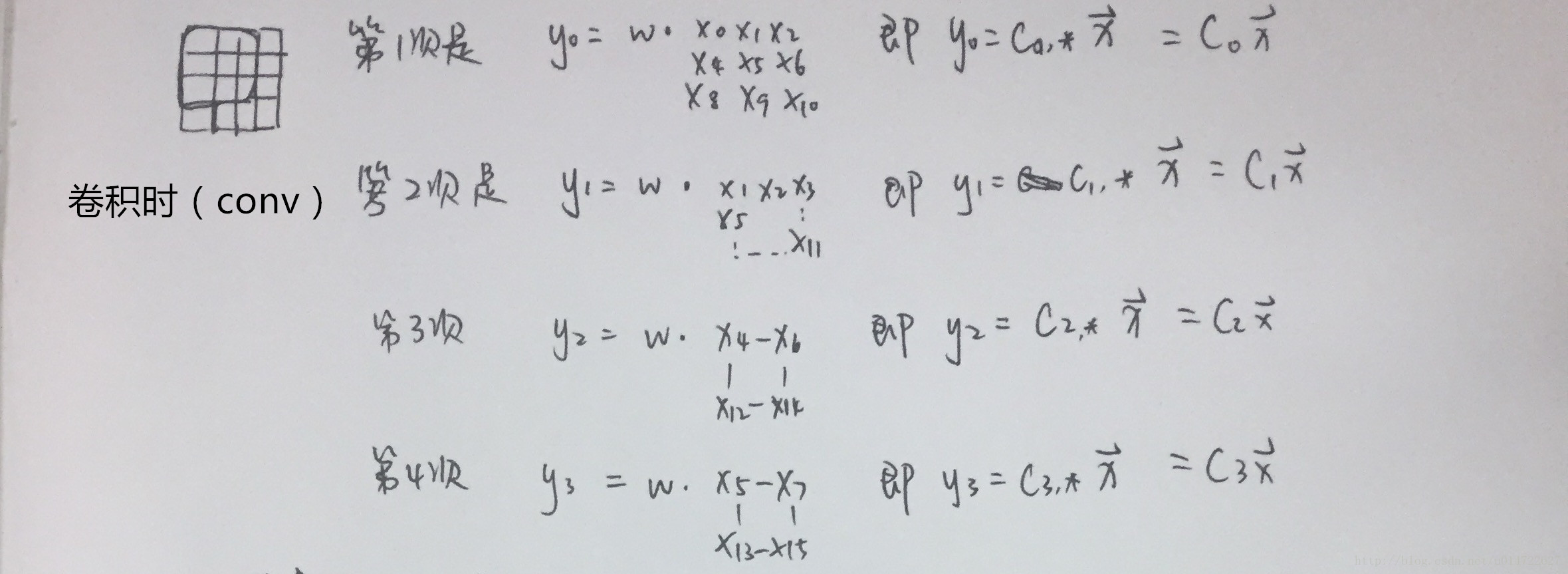深度学习卷积网络中反卷积/转置卷积的理解 transposed conv/deconv
搞明白了卷积网络中所谓deconv到底是个什么东西后,不写下来怕又忘记,根据参考资料,加上我自己的理解,记录在这篇博客里。
先来规范表达
- 为了方便理解,本文出现的举例情况都是2D矩阵卷积,卷积输入和核形状都为正方形,x和y轴方向的padding相同,stride也相同。
- 记号:
i,o,k,p,s i,o,k,p,s 分别表示:卷积/反卷积的输入大小 input size input size,卷积/反卷积输出大小 output size output size,卷积/反卷积核大小 kernel size kernel size, padding padding, stride stride 。 - 举例(如下左图):
输入 X∈R(4,4) X∈R(4,4)矩阵,卷积核 w∈R(3,3),padding=0,stride=1 w∈R(3,3),padding=0,stride=1的情况下,卷积的输出 Y∈R(2,2) Y∈R(2,2),就记为 i=4,o=2,k=3,p=0,s=1 i=4,o=2,k=3,p=0,s=1 。
推翻错误的理解
第一次看到deconv这个词,以为deconv的结果就是卷积的逆,觉得神奇,不禁产生了“哦?转置的卷积就可以求逆了吗?”这样的想法,然后在matlab里面实验求证,我还记得当时以为反卷积能够求逆,考虑到图片进行常规卷积操作输出大小又不可能变大(same/valid),于是我还假设反卷积输出大小不变,用了same padding和原核的转置作为反卷积配置,结果发现根本不是那么一回事好吗。
其实DL中的deconv,是一种上采样过程,举个比方:输入 X∈R(4,4) X∈R(4,4)矩阵,卷积核 w∈R(3,3),pad=0,stride=1 w∈R(3,3),pad=0,stride=1的情况下(如下左图),卷积的输出 Y∈R(2,2) Y∈R(2,2)。对 Y Y进行deconv,它只能做到把还原输出大小到和 X X一样大,输出值和 X X有那么一点联系。
所以啊deconv这个名字相当误导人呐!这在cs231n课程里也被吐槽过,大家现在更喜欢用transposed conv来表述反卷积。为了方便起见,后文就用反卷积这个词了。
第二个容易confused的地方,就是很多文章都说卷积核的转置就可以求反卷积,又陷入迷茫“就算把卷积核转置(或者左右翻转上下翻转),卷积后输出还是越来越小(或不变,至少不会增大)啊”……直到看到文献和相应的这个动画(其他动画在github-convolution arithmetic1)
 |
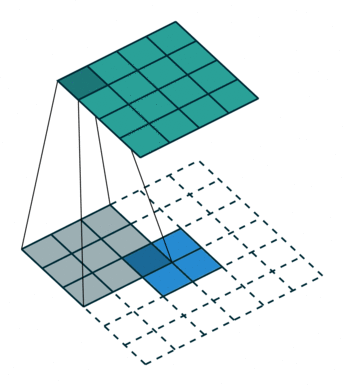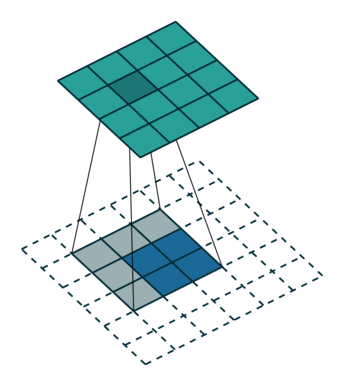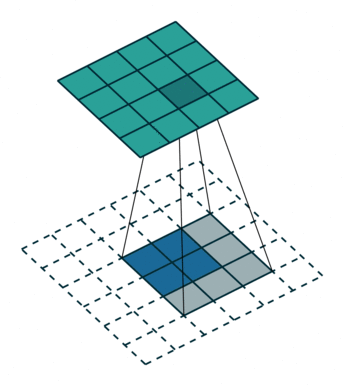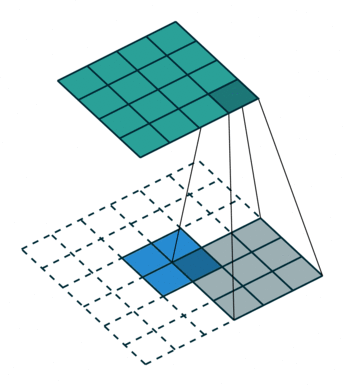 |
|---|---|
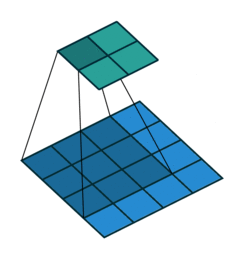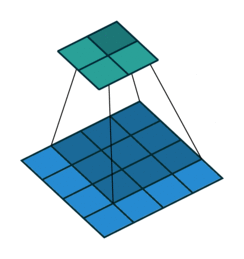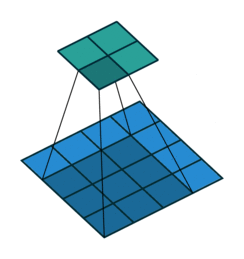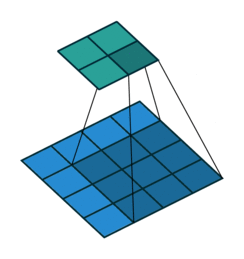
| 卷积 i=4,k=3,p=0,s=1,则 o=2 i=4,k=3,p=0,s=1,则 o=2 | 反卷积 i=2,k=3,p=0,s=1,则 o=4 i=2,k=3,p=0,s=1,则 o=4 |
注意图中蓝色(下面)是输入,绿色(上面)是输出,卷积和反卷积在 p、s、k p、s、k 等参数一样时,是相当于 i i 和 o o 调了个位。
这里说明了反卷积的时候,是有补0的,即使人家管这叫no padding( p=0 p=0),这是因为卷积的时候从蓝色 4×4 4×4 缩小为绿色 2×2 2×2,所以对应的 p=0 p=0 反卷积应该从蓝色 2×2 2×2 扩展成绿色 4×4 4×4。而且转置并不是指这个 3×3 3×3 的核 w w 变为 wT wT,但如果将卷积计算写成矩阵乘法(在程序中,为了提高卷积操作的效率,就可以这么干,比如tensorflow中就是这种实现), Y⃗ =CX⃗ Y→=CX→(其中 Y⃗ Y→ 表示将 Y⃗ Y→ 拉成一维向量, X⃗ X→ 同理),那么反卷积确实可以表示为 CTY⃗ CTY→,而这样的矩阵乘法,恰恰等于 w w 左右翻转再上下翻转后与补0的 Y Y卷积的情况。
然后就产生了第三个confuse:“补0了会不会有影响,还能通过反卷积近似输入 X X 吗?”其实反卷积也不一定能达到近似的效果,图像里的卷积,相当于一种相关操作,而反卷积维持了这种相关操作时的 w w 与 X X、与 Y Y 之间的联系维持了。至于补0后操作是否还等价,上一段已经说明了是等价的,读者可以在阅读完后面的文章后自己尝试一下。
反卷积以及反向传播的过程
卷积和反卷积的过程在arXiv-A guide to convolution arithmetic for deep learning2写的非常详细,还有很多例子便于理解,在这里我就截图出重点来(ps.文中的figure2.1就是上图的左边)。剩下的例子请大家多看看原文,最好自己动手算一下,我也贴个我算的过程( Ci Ci 表示矩阵 C C 的第 i i 行),供参考。
关于反向传播, 知乎-如何理解深度学习中的deconvolution networks3有详细的推导过程。 


深度学习卷积网络中反卷积/转置卷积的理解 transposed conv/deconv的更多相关文章
- CVPR2020:点云分析中三维图形卷积网络中可变形核的学习
CVPR2020:点云分析中三维图形卷积网络中可变形核的学习 Convolution in the Cloud: Learning Deformable Kernels in 3D Graph Con ...
- 吴恩达深度学习笔记(deeplearning.ai)之卷积神经网络(一)
Padding 在卷积操作中,过滤器(又称核)的大小通常为奇数,如3x3,5x5.这样的好处有两点: 在特征图(二维卷积)中就会存在一个中心像素点.有一个中心像素点会十分方便,便于指出过滤器的位置. ...
- 吴恩达深度学习笔记(deeplearning.ai)之卷积神经网络(CNN)(上)
作者:szx_spark 1. Padding 在卷积操作中,过滤器(又称核)的大小通常为奇数,如3x3,5x5.这样的好处有两点: 在特征图(二维卷积)中就会存在一个中心像素点.有一个中心像素点会十 ...
- 卷积网络中的通道(Channel)和特征图
转载自:https://www.jianshu.com/p/bf8749e15566 今天介绍卷积网络中一个很重要的概念,通道(Channel),也有叫特征图(feature map)的. 首先,之前 ...
- 【AI in 美团】深度学习在OCR中的应用
AI(人工智能)技术已经广泛应用于美团的众多业务,从美团App到大众点评App,从外卖到打车出行,从旅游到婚庆亲子,美团数百名最优秀的算法工程师正致力于将AI技术应用于搜索.推荐.广告.风控.智能调度 ...
- 【腾讯Bugly干货分享】深度学习在OCR中的应用
本文来自于腾讯bugly开发者社区,未经作者同意,请勿转载,原文地址:http://dev.qq.com/topic/5809bb47cc5e52161640c5c8 Dev Club 是一个交流移动 ...
- 【深度学习】CNN 中 1x1 卷积核的作用
[深度学习]CNN 中 1x1 卷积核的作用 最近研究 GoogLeNet 和 VGG 神经网络结构的时候,都看见了它们在某些层有采取 1x1 作为卷积核,起初的时候,对这个做法很是迷惑,这是因为之前 ...
- Attention机制在深度学习推荐算法中的应用(转载)
AFM:Attentional Factorization Machines: Learning the Weight of Feature Interactions via Attention Ne ...
- 深度学习训练过程中的学习率衰减策略及pytorch实现
学习率是深度学习中的一个重要超参数,选择合适的学习率能够帮助模型更好地收敛. 本文主要介绍深度学习训练过程中的6种学习率衰减策略以及相应的Pytorch实现. 1. StepLR 按固定的训练epoc ...
随机推荐
- shiro学习总结(一)----初识shiro
本系列内容大多总结自官网和张开涛的<跟我学Shiro> 一.shiro简介 1.1.shiro有什么用? shiro是一个功能强大使用简单的java安全框架,主要提供了五大功能: 1.认证 ...
- ServletContextListener使用详解(监听Tomcat启动、关闭)
在 Servlet API 中有一个 ServletContextListener 接口,它能够监听 ServletContext 对象的生命周期,实际上就是监听 Web 应用的生命周期. 当Serv ...
- 创建emlog
第一步:解压安装包并且安装 第二步:打开phpstudy,并启动(如果安装后打开显示没有VC11,则要去安装) 第三步:打开“其他管理项菜单”下面的“根目录”,将emlog下面的emlog之下的全部文 ...
- C#相关FTP操作
C# 相关 FTP(File Transfer Protocol) 操作 1.获取文件目录 UsePassive:需要设置为false. 使用被动模式,因为客户端防火墙的存在,所以为了确保数据可以正常 ...
- Java并发编程(十二)-- 阻塞队列
在介绍Java的阻塞队列之前,我们简单介绍一下队列. 队列 队列是一种数据结构.它有两个基本操作:在队列尾部加人一个元素,和从队列头部移除一个元素就是说,队列以一种先进先出的方式管理数据,如果你试图向 ...
- 纯js上传文件 很好用
<!DOCTYPE html> <html> <head> <meta charset="utf-8"> <meta name ...
- ES6 对对象的扩展
1.对象类别 普通对象:具有JavaScript对象的所有默认内部行为 特异对象: 具有某些与默认行为不符的内部行为 标准对象: ECMAScript 6 规范中新定义的对象,例如Array,Date ...
- hdu 6034 B - Balala Power! 贪心
B - Balala Power! 题目链接 http://acm.hdu.edu.cn/showproblem.php?pid=6034 题面描述 Talented Mr.Tang has n st ...
- win7 64位安装opencv3.0
一.去官网下载opencv3.0 下载Win pack,下载后解压,自己在D盘下新建了文件夹OpenCV3.3_win D:\OpenCV3.3_win,把下载到的Win pack解压到里面.解压或者 ...
- elastic-job详解(二):作业的调度
JobScheduler是elastic-job作业调度的关键类,也是起始类,在包com.dangdang.ddframe.job.lite.api下.调度任务的执行需要包含两大步骤:任务的配置和任务 ...