$Matrix-Tree$定理-题目

$Matrix-Tree$

　　其实矩阵树的题挺好玩的，一些是套班子求答案的，也有一些题目是靠观察基尔霍夫矩阵性质推式子的。

　　

　　文艺计算姬：https://www.lydsy.com/JudgeOnline/problem.php?id=4766

　　题意概述：求完全二分图的生成树数目。左部点的个数为n，右部为m，答案对p取模。$n,m,p<=10^{18}$

　　好玩的题目！刚看到这个题的时候以为是一道板子题，看了一眼数据范围...对于完全二分图，基尔霍夫矩阵是非常有特点的(删掉最后一行最后一列)，首先看对角线，前n行为m，后m-1行为n。右上角和左下角各是一个$ n \times (m-1)$的$-1$块。手动消元一番，发现答案是$n^{m-1}m^{n-1}$，但是消到下半部分只能靠找规律，没有严谨的证明。交上去虽然A了，但是总觉得这个做法不是很靠谱，于是又学了一种非常科学的方法：

　　抛弃原始的按行消元，而是利用特殊的性质。将除第 $n$ 行以外的行加进第 $n$ 行里，此时第 $n$ 行变成这个样子：

　　

　　此时第 $n+1$ 行往下是长这个样子的：

　　

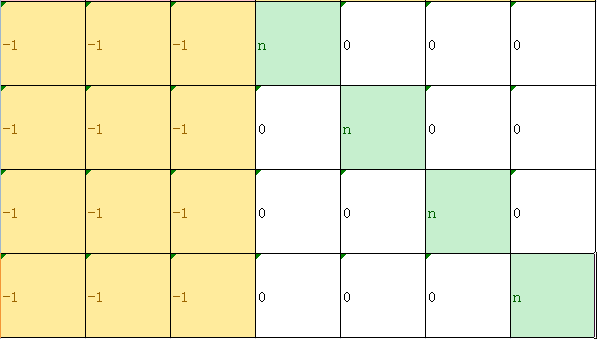
　　把之前消出来的那一行分别加到这些行里面，就只剩下绿色部分了，就像这样：

　　

　　问题是这个奇怪的矩阵的行列式怎么求啊？看一看最早的定义式：

　　${det(K)=}\sum_{P}^{ }\;{(}{(-1)}^{\tau{(P)}}\times{K}_{1,p1}\times{K}_{2,p2}\times{K}_{3,p3}\times\cdots\times{K}_{N,pN}{)}$

　　显然每行每列只能选一个数出来，对于前 $n-1$ 列，如果选了 $n$ 行的1，第 $n$ 列就没得选了，所以如果想求有意义的答案，第 $n$ 行必然要选第 $n$ 个数，剩下每行的证明同理，所以这个矩阵的行列式求法等同于上三角矩阵，答案就是 $n^{m-1}m^{n-1}$ 有了准确的证明后感觉非常快乐.

　　

 # include <cstdio>
 # include <iostream>
 # define ll long long

 using namespace std;

 ll n,m,p,ans=;

 ll mul (ll a,ll b)
 {
     ll s=;
     while(b)
     {
         if(b&1LL) s=(a+s)%p;
         a=(a+a)%p;
         b>>=1LL;
     }
     return s%p;
 }

 ll qui (ll a,ll b)
 {
     ll s=;
     while(b)
     {
         if(b&1LL) s=mul(a,s);
         a=mul(a,a);
         b>>=1LL;
     }
     return s%p;
 }

 int main()
 {
     scanf("%lld%lld%lld",&n,&m,&p);
     ans=mul(ans,qui(m,n-));
     ans=mul(ans,qui(n,m-));
     printf("%lld",ans);
     return ;
 }

文艺计算姬

　　小Z的房间：https://www.lydsy.com/JudgeOnline/problem.php?id=4031

　　题意概述：求模 $10^9$ 意义下的生成树个数。$n<=90$

　　就是一道矩阵树模板题啦，只是模数不是质数有一点难办。回想矩阵树定理，有这样的性质：

　　“将两行进行交换，答案取反”；“将一行的k倍加到另一行里，答案不变”

　　所以就有了一种新的算法：数列欧几里得！

　　其实就是只关注每行要消去的那个数，将两行辗转相除，总复杂度是 $O(N^3loga_i)$.

　　

 # include <cstdio>
 # include <iostream>
 # include <cstring>
 # define R register int
 # define ll long long 

 using namespace std;

 const int mod=;
 const int maxn=;
 int n,m,id[maxn][maxn],cnt;
 ll K[maxn][maxn];
 char s[maxn];

 int ab (int x) { if(x<) return -x; return x; }

 int Gauss ()
 {
     ll t,ans=;
     for (R i=;i<=n;++i)
           for (R j=;j<=n;++j)
               K[i][j]=(K[i][j]%mod+mod)%mod;
     for (R i=;i<=n;++i)
     {
         for (R j=i+;j<=n;++j)
         {
             while(K[j][i])
             {
                 t=K[i][i]/K[j][i];
                 for (R k=i;k<=n;++k)
                     K[i][k]=(K[i][k]-K[j][k]*t%mod)%mod;
                 swap(K[i],K[j]);
                 ans*=-;
             }
         }
         ans=1LL*K[i][i]*ans%mod;;
     }
     return (ans%mod+mod)%mod;
 }

 int main()
 {
     scanf("%d%d",&n,&m);
     for (R i=;i<=n;++i)
     {
         scanf("%s",s+);
         for (R j=;j<=m;++j)
         {
             if(s[j]=='*') continue;
             id[i][j]=++cnt;
             if(id[i-][j])
             {
                 K[ id[i-][j] ][ id[i-][j] ]++;
                 K[ id[i][j] ][ id[i][j] ]++;
                 K[ id[i-][j] ][ id[i][j] ]--;
                 K[ id[i][j] ][ id[i-][j] ]--;
             }
             if(id[i][j-])
             {
                 K[ id[i][j-] ][ id[i][j-] ]++;
                 K[ id[i][j] ][ id[i][j] ]++;
                 K[ id[i][j-] ][ id[i][j] ]--;
                 K[ id[i][j] ][ id[i][j-] ]--;
             }
         }
     }
     n=cnt-;
     printf("%d",Gauss());
     return ;
 }

小Z的房间

　　重建：https://www.lydsy.com/JudgeOnline/problem.php?id=3534

　　题意概述：给定一张图，每条边有 $p\%$ 的概率出现，求出现的边恰好构成一棵生成树的概率。

　　从另一个方向理解矩阵树定理，发现它求的是这么一个式子：

　　$\sum_T\prod_{e \in T} \omega_e$

　　这就很有启发性了...将边权改为边的出现概率，那么一棵树生成的概率就是所有边出现的概率的乘积...吗？其实并不是，构成一个树不仅需要这些边出现，还得要求别的边都不出现才行，于是有了这样的式子：

　　$\sum_T\prod_{e \in T} \omega_e \prod_{e \notin T} (1-\omega_e)$

　　但是这样的式子能求吗？正面求是不行的，我们只能求“属于”的，所以需要想办法让式子里消掉“不属于”的部分。这怎么做呢？容斥呀。

　　$\prod_(1-\omega_e)\sum_T\prod_{e \in T} \frac{\omega_e}{1-\omega_e}$

　　把式子进行这样的变形后，需要用矩阵树求的值就只与“属于”树的边有关了，到这里再套板子就行。如果一条边存在的概率是一，那么就将它稍微调小一点点，否则会出现除以 $0$ 的情况。这题算的是相对误差，所以有点卡精度，首先eps要设到$10^{-10}$，输出时也要输出10位小数才可以。

　　

 # include <cstdio>
 # include <iostream>
 # include <cmath>
 # include <algorithm>
 # define R register int

 using namespace std;

 const double eps=1e-;
 const int maxn=;
 int n;
 double K[maxn][maxn],S=;

 double Gauss()
 {
     n--;
     double ans=,t;
     int maxx;
     for (R i=;i<=n;++i)
     {
         maxx=i;
         for (R j=i+;j<=n;++j) if(fabs(K[j][i])>fabs(K[maxx][i])) maxx=j;
         if(maxx!=i) ans*=-,swap(K[i],K[maxx]);
         for (R j=i+;j<=n;++j)
         {
             t=K[j][i]/K[i][i];
             for (R k=i;k<=n;++k)
                 K[j][k]-=K[i][k]*t;
         }
         ans*=K[i][i];
     }
     return fabs(ans*S);
 }

 int main()
 {
     scanf("%d",&n);
     for (R i=;i<=n;++i)
         for (R j=;j<=n;++j)
             scanf("%lf",&K[i][j]);
     for (R i=;i<=n;++i)
         for (R j=;j<=n;++j)
         {
             if(i==j) continue;
             if(K[i][j]==) K[i][j]-=eps;
             if(i<j) S*=(-K[i][j]);
             K[i][i]+=K[i][j]/(-K[i][j]);
             K[i][j]=K[i][j]/(K[i][j]-);
         }
     printf("%.10lf",Gauss());
     return ;
 }

重建

　　社交网络：https://www.lydsy.com/JudgeOnline/problem.php?id=5297

　　题意概述：求一张有向图上的外向生成树个数(给定根),n<=250;

　　CQOI好奇怪...尤其是18年的题都不是很难，考察的点是卡常？

　　这是一道比较有趣的矩阵树,朴素的矩阵树可以解决无向图的生成树问题，有向图其实也差别不大。首先邻接矩阵是不变的-> $a[i][j]$ 表示 $i$ 到 $j$ 的连边情况；

　　外向树：边由根指向叶子，度数矩阵存入度； 内向树：边由叶子指向根，度数矩阵存出度；

　　求矩阵树首先需要删掉一行一列，如果指定了根，就必须删掉根所在的行列了。

　　

 # include <cstdio>
 # include <iostream>
 # define R register int

 using namespace std;

 const int maxn=;
 const int mod=;
 int n,m,x,y,a[maxn][maxn];

 int qui (int a,int b)
 {
     int s=;
     while(b)
     {
         if(b&) s=s*a%mod;
         a=a*a%mod;
         b>>=;
     }
     return s;
 }

 int Gauss ()
 {
     int ans=,maxx;
     for (R i=;i<=n;++i)
     {
         maxx=i;
         for (R j=i;j<=n;++j) if(a[j][i]>a[maxx][i]) maxx=j;
         if(maxx!=i) swap(a[i],a[maxx]),ans=mod-ans;
         for (R j=i+;j<=n;++j)
         {
             if(!a[j][i]) continue;
             int t=a[j][i]*qui(a[i][i],mod-)%mod;
             for (R k=i;k<=n;++k)
                 a[j][k]=(a[j][k]-a[i][k]*t%mod+mod)%mod;
         }
         ans=ans*a[i][i]%mod;
         if(ans<) ans+=mod;
     }
     return (ans%mod+mod)%mod;
 }

 int main()
 {
     scanf("%d%d",&n,&m);
     for (R i=;i<=m;++i)
     {
         scanf("%d%d",&x,&y);
         a[y][x]--; a[x][x]++;
     }
     for (R i=;i<=n;++i)
         for (R j=;j<=n;++j)
             a[i][j]=(a[i][j]%mod+mod)%mod;
     printf("%d",Gauss());
     return ;
 }

社交网络

---shzr