AI 线性代数

1、标量、向量、矩阵和张量

1）标量（scalar），一个数，例如自然数和实数。

2）向量（vector），一列有序数。可以看作只有一列的矩阵。

3）矩阵（matrix），二维数组。转置（transpose），关于主对角线（从左上角到右下角）对称。

4）张量（tensor），高维数组。

2、矩阵和向量相乘

1）矩阵乘法，（m x n）(n x p) = （m x p）

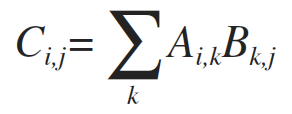
2）向量点积

3、单位矩阵和矩阵逆

1）单位矩阵（identity matrix），任意向量和单位矩阵相乘都不会变。

2）矩阵逆（matrix inversion），

4、线性相关和生成子空间

5、范数（norm）

衡量向量大小的函数。

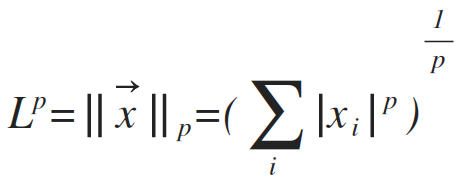
p=2，欧几里得范数（Euclidean norm）。

7、特征分解

特征分解（eigendecomposition），将矩阵分解成特征向量和特征值。

方阵A的特征向量（eigenvector），与A相乘等于对该向量进行缩放。

推导过程：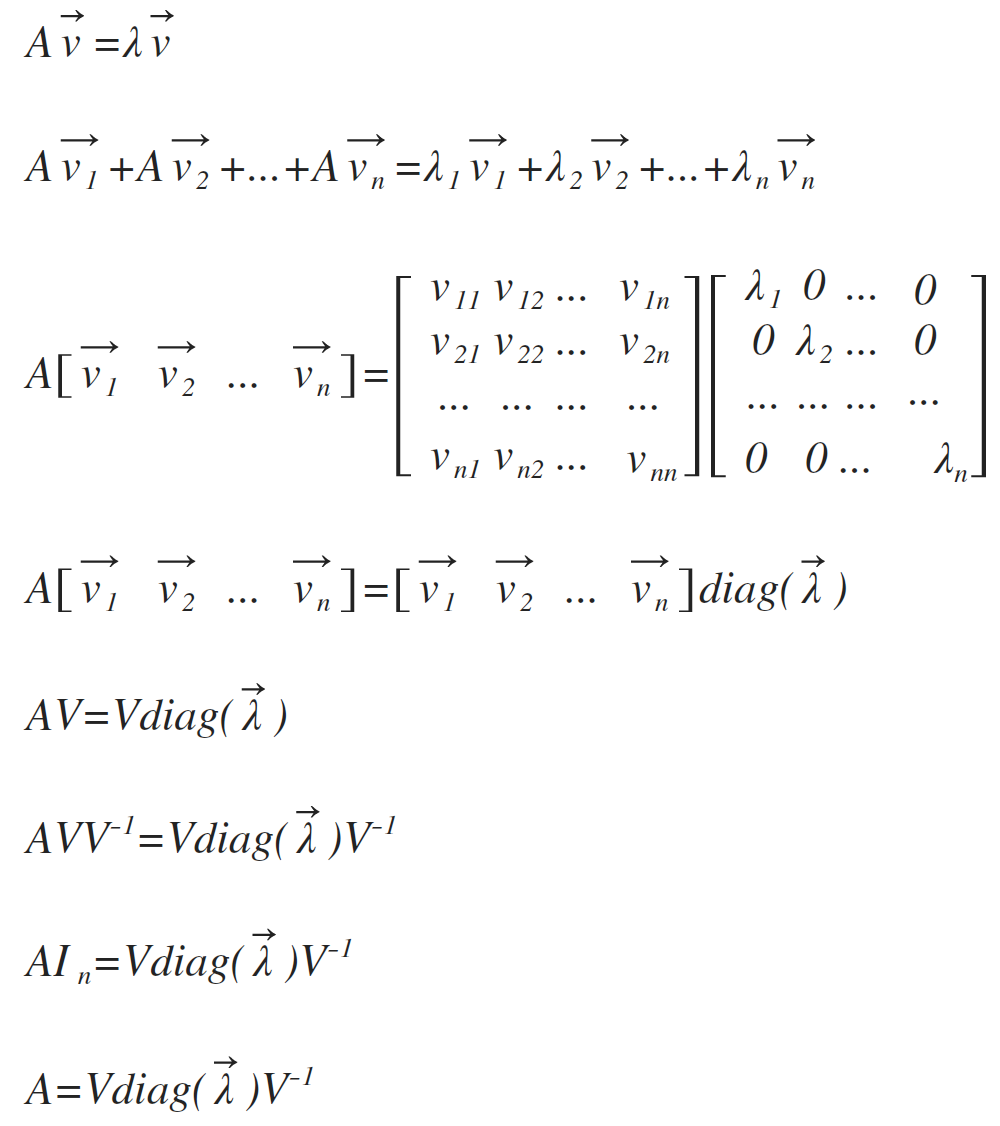 

8、奇异值分解

10、迹运算

1）迹运算（trace），矩阵主对角线元素的和

2）迹运算等于转置的迹运算

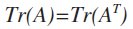
11、行列式

det(A)，将方阵A映射到实数，等于矩阵特征值的乘积。

1）二阶行列式

2）几何意义

两个向量（行向量或者列向量）形成的平行四边形的面积。高阶行列式则表示平行多面体的体积。

3）线性变换

方阵可以表示线性变换。行列式是线性变换的伸缩因子。

正交矩阵

参考链接：

http://baijiahao.baidu.com/s?id=1598899137339626314&wfr=spider&for=pc

https://baike.baidu.com/item/%E4%B8%89%E8%A7%92%E5%87%BD%E6%95%B0%E5%85%AC%E5%BC%8F/4374733

https://jingyan.baidu.com/article/acf728fd78dc4ef8e510a3f4.html