素数问题三步曲_HDOJ2098

偶然间OJ上敲到一题素数问题便查询了相关算法。对于该类问题我个人学习分为三步曲：最笨的方法（TLE毫无疑问）->Eratosthrnes筛选法->欧拉线性筛选法

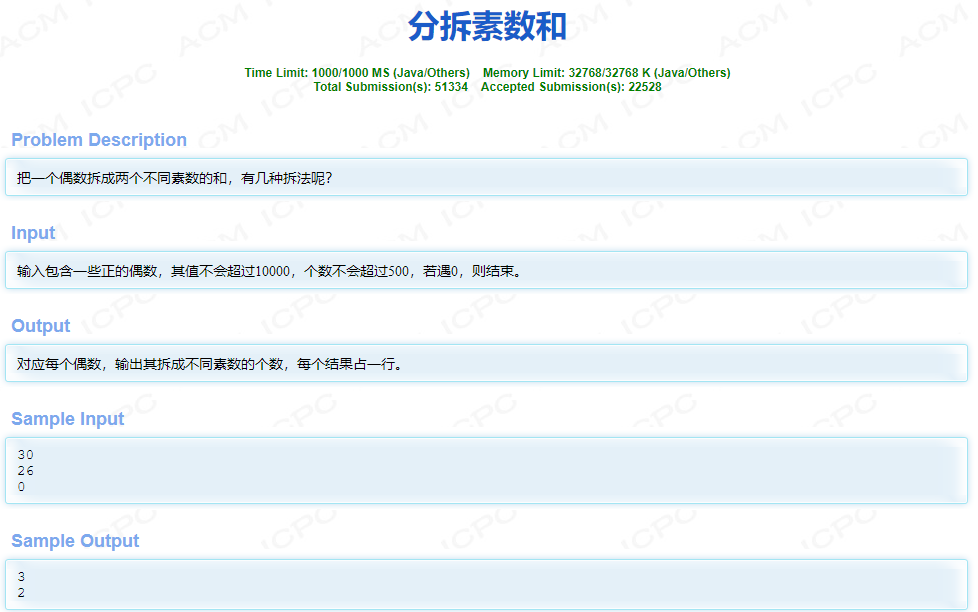
针对HDOJ2098这道题进行代码分析，发散性可以解决其他问题。

笨笨的方法（TLE）

#include<stdio.h>
#include<stdlib.h>
#include<string.h>

int main()
{
	int a,b,n;
	while(1)
	{
		scanf("%d",&n);
//		printf("这是输入的数：%d\n",n);
		if(n==0) break;
		int i=1,sum=0;
		for(i=2;i<n/2;i++)
		{
			//判断i,n-i两者是否都是素数
			int j=2,flag=0;
			for(j=2;j<=i/2;j++)
			{
				if(i%j==0)
				{
					flag=1;
					break;
				}
			}
//			printf("第一次判断i是否为素数结束\n");
			for(j=2;j<=(n-i)/2;j++)
			{
				if((n-i)%j==0||(n-i)==1)
				{
					flag=1;
					break;
				}
			}
//			printf("第二次判断n-i是否为素数结束\n");
			if(flag==0)
			{
//				printf("此时i和n-i都是素数：%d %d\n",i,n-i);
				sum++;
			}
		}
		printf("%d\n",sum);
	}
	return 0;
}

Eratorsthenes筛选法（AC）

#include<stdio.h>
#include<stdlib.h>
#include<math.h>
#include<string.h>

#define MAX 100000
bool num[10000]={false,false,true};

int main()
{
	int n;
	int i=0,j=0;
	for(i=3;i<10000;i++)
	{
		//初始化所有的数都为素数
		num[i]=true;
	}

	//从2开始对所有素数的倍数置为false
	for(i=2;i*i<10000;i++)
	{
		if(num[i]==true)
		{
			for(j=i*i;j<10000;j+=i)
			{
				num[j]=false;
			}
		}
	}
	//检测输出所有比10000小的素数序列
//	for(i=1;i<10000;i++)
//	{
//		if(num[i]==true)
//			printf("%d ",i);
//	}

	while(1)
	{
		int cnt=0;
		scanf("%d",&n);
		if(n==0) break;

		for(i=2;i<n/2;i++)
		{
			if(num[i]==true&&num[n-i]==true)
			{
				cnt++;
			}
		}
		printf("%d\n",cnt);
	}
	return 0;
}

Eratorsthenes筛选法（复杂度nlogn）是素数问题中十分有名的解法：即要求N以下的所有为素数的数有多少个？我们需要检查到sqrt(n)是否存在素数即可。

1. 假设有一个筛子存放1~N的数。2 3 4 5 6 7 8 9 10 11 12 ...N
2. 先将2的倍数筛选出去（一定不为素数）2 3 5 7 9 11 13 17 19...N
3. 将3的倍数筛选出去（一定不为素数）2 3 5 7 11 13 17 19...N
4. 即不断对当前剩下的数列中最前面的数的倍数从数列中筛选出去，最后剩下的数列即为所有比N小的素数序列。

欧拉线性筛选法

我们可以发现在Eratorthenes筛选法中，30,这个数，在215中被筛了一次，在56中又被重复筛了，所以对于此处可以进行优化修改。但是我对于其中算法关键看了一会不是很懂，目前就暂时不写吧。