数据库的范式,第一、二、三、四、五范式、BC范式
数据库的规范化(上一篇博客有写到)的程度不同,便有了这么多种范式。数据库范式是数据库设计必不可少的知识,没有对范式的理解,就无法设计出高效率、优雅的数据库,甚至设计出错误误的数据库。课本中的定义比较抽象,不太直观,也不易理解,记是肯定记不住的。
关系数据库
常用范式
关系数据库知道了,再来理解范式。范式是关系数据库关系模式规范化的标准,从规范化的宽松到严格,分为不同的范式,通常使用的有第一范式。第二范式、第三范式及BC范式。范式是建立在函数依赖基础上的。
函数依赖
如果一个表中某一个字段Y的值是由另外一个字段或一组字段X的值来确定的,就称为Y函数依赖于X。
函数依赖
定义
设X,Y是关系R的两个属性集合,当任何时刻R中的任意两个元组中的X属性值相同时,则它们的Y属性值也相同,则称X函数决定Y,或Y函数依赖于X。3.平凡函数依赖当关系中属性集合Y是属性集合X的子集时(Y⊆X),存在函数依赖X→Y,即一组属性函数决定它的所有子集,这种函数依赖称为平凡函数依赖。4.非平凡函数依赖当关系中属性集合Y不是属性集合X的子集时,存在函数依赖X→Y,则称这种函数依赖为非平凡函数依赖。5.完全函数依赖设X,Y是关系R的两个属性集合,X’是X的真子集,存在X→Y,但对每一个X’都有X’!→Y,则称Y完全函数依赖于X。6.部分函数依赖设X,Y是关系R的两个属性集合,存在X→Y,若X’是X的真子集,存在X’→Y,则称Y部分函数依赖于X。7.传递函数依赖设X,Y,Z是关系R中互不相同的属性集合,存在X→Y(Y !→X),Y→Z,则称Z传递函数依赖于X。属性关系
属性之间有三种关系,但并不是每一种关系都存在函数依赖。设R(U)是属性集U上的关系模式,X、Y是U的子集:● 如果X和Y之间是1:1关系(一对一关系),如学校和校长之间就是1:1关系,则存在函数依赖X → Y和Y →X。● 如果X和Y之间是1:n关系(一对多关系),如年龄和姓名之间就是1:n关系,则存在函数依赖Y → X。●如果X和Y之间是m:n关系(多对多关系),如学生和课程之间就是m:n关系,则X和Y之间不存在函数依赖。案例分析
编辑
例: Student(Sno, Sname, Ssex, Sage, Sdept)
假设不允许重名,则有:
Sno → Ssex, Sno → Sage , Sno → Sdept,
Sno ←→ Sname, Sname → Ssex, Sname → Sage
Sname → Sdept
但Ssex -\→ Sage
若 X → Y,并且 Y → X, 则记为 X ←→ Y。
若 Y 不函数依赖于 X, 则记为 X -\→ Y。
在关系模式R(U)中,对于U的子集X和Y,
1.如果 X → Y,但 Y 不为 X 的子集,则称 X → Y 是非平凡的函数依赖
例:在关系SC(Sno, Cno, Grade)中,
非平凡函数依赖: (Sno, Cno) → Grade。
2.若 X → Y,但 Y 为 X 的子集, 则称 X → Y 是平凡的函数依赖
平凡函数依赖: (Sno, Cno) → Sno ,(Sno, Cno) → Cno。
3.若 x → y 并且,存在 x 的真子集 x1,使得 x1 → y, 则 y 部分依赖于 x。
例:学生表(学号,姓名,性别,班级,年龄)关系中,
部分函数依赖:(学号,姓名)→ 性别,学号 → 性别,所以(学号,姓名)→ 性别 是部分函数依赖。
4.若 x → y 并且,对于 x 的任何一个真子集 x1,都不存在 x1 → y 则称y完全依赖于x。
例:成绩表(学号,课程号,成绩)关系中,
完全函数依赖:(学号,课程号)→ 成绩,学号 -\→ 成绩,课程号 -\→ 成绩,所以(学号,课程号)→ 成绩 是完全函数依赖。
5.若x → y并且y → z,而y -\→ x,则有x → z,称这种函数依赖为传递函数依赖。
例:关系S1(学号,系名,系主任),
学号 → 系名,系名 → 系主任,并且系名 -\→ 学号,系主任 -\→ 系名,所以学号 → 系主任为传递函数依赖。
范式间的关系
1NF
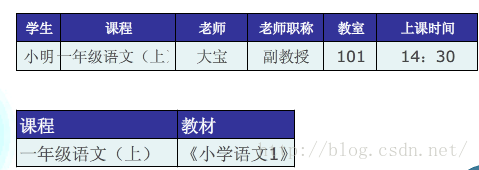
2NF

(学生,课程)——>上课时间;
- (学生,课程)是一个码,课程却决定了教材,这就叫做不完全依赖,或者说部分依赖。
出现了这种情况,就不满足第二范式了。
解决办法:分解。进行投影分解:
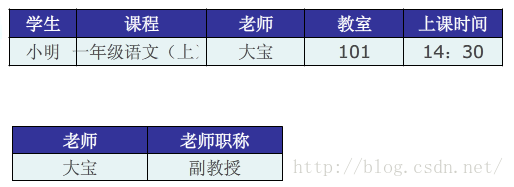
3NF
如果关系模式R是2NF,且关系模式R(U,F)中的所有非主属性对任何候选关键字都不存在传递依赖,则称关系R是属于第三范式。第三范式(3NF);符合2NF,并且,消除传递依赖。上图中符合2NF ,但存在传递依赖(老师——>老师职称。一个老师一定能确定一个老师职称)。解决办法:分解。投影分解:其他范式
第四范式:要求把同一表内的多对多关系删除。第五范式:从最终结构重新建立原始结构。BC范式(BCNF):符合3NF,并且,主属性不依赖于主属性。若关系模式R属于第一范式,且每个属性都不传递依赖于键码,则R属于BC范式。
数据库的范式,第一、二、三、四、五范式、BC范式的更多相关文章
- 6月29-7月5日成都uber优步司机第一/二/三组奖励政策明细
成都优步司机第一/二/三组奖励更新了,在写下文之前,我先吐槽一下:靠优步uber发财致富已成往事. 滴滴快车单单2.5倍,注册地址:http://www.udache.com/如何注册Uber司机(全 ...
- 使用MongoDB数据库(1)(三十五)
MongoDB简介 MongoDB是一个基于分布式文件存储的数据库,它是一个介于关系数据库和非关系数据库之间的产品,其主要目标是在键/值存储方式(提供了高性能和高度伸缩性)和传统的RDBMS系统(具有 ...
- 第一百三十五节,JavaScript,封装库--拖拽
JavaScript,封装库--拖拽 封装库新增1个拖拽方法 /** tuo_zhuai()方法,将一个弹窗元素实现拖拽功能 * 注意:一般需要在css文件将元素里的某一个区块光标设置成提示可以拖拽, ...
- 第三百二十四节,web爬虫,scrapy模块介绍与使用
第三百二十四节,web爬虫,scrapy模块介绍与使用 Scrapy是一个为了爬取网站数据,提取结构性数据而编写的应用框架. 其可以应用在数据挖掘,信息处理或存储历史数据等一系列的程序中.其最初是为了 ...
- C语言探索之旅】 第一部分第四课第三章:变量的世界之显示变量内容
内容简介 1.课程大纲 2.第一部分第四课第三章:变量的世界之显示变量内容 3.第一部分第五课预告:基本运算 课程大纲 我们的课程分为四大部分,每一个部分结束后都会有练习题,并会公布答案.还会带大家用 ...
- 程序员与年龄:四十岁普通开发、三十五岁首席架构、三十岁基层Leader
最近,有一个词儿特别热门--躺平.有没有人跟你说过:"躺平说起来容易,做起来更容易." 和躺平相对的是另外一个词--内卷,群聊的时候,已经很多次看过草卷起来了.jpg表情包.某些节 ...
- SQL注入之Sqli-labs系列第三十四关(基于宽字符逃逸POST注入)和三十五关
开始挑战第三十四关和第三十五关(Bypass add addslashes) 0x1查看源码 本关是post型的注入漏洞,同样的也是将post过来的内容进行了 ' \ 的处理. if(isset($_ ...
- 第三百五十四节,Python分布式爬虫打造搜索引擎Scrapy精讲—数据收集(Stats Collection)
第三百五十四节,Python分布式爬虫打造搜索引擎Scrapy精讲—数据收集(Stats Collection) Scrapy提供了方便的收集数据的机制.数据以key/value方式存储,值大多是计数 ...
- NeHe OpenGL教程 第三十五课:播放AVI
转自[翻译]NeHe OpenGL 教程 前言 声明,此 NeHe OpenGL教程系列文章由51博客yarin翻译(2010-08-19),本博客为转载并稍加整理与修改.对NeHe的OpenGL管线 ...
随机推荐
- ES集群
1. ElasticSerach集群安装 修改配置文件elasticserach.yml [elk@localhost config]$ vi elasticsearch.yml # ------- ...
- 062 SparkStream内部原理
1.DStream 内部是一系列的RDD组成的,每个RDD与RDD的产生时间形成一个pair保存在内存中(下面有) RDD包含了对应时间段的所有block数据. 2.DStream下的方法 /** T ...
- STL容器及泛型算法
一.顺序容器 1.容器的选择 (1) 随机访问,选vector ,deque (2) 在中间插入或者删除元素,选list (3) 在头尾插入或删除元素 , 选deque 2.list的成员函数 (1) ...
- appium-电脑连不上手机设备如何解决
在自动化过程中,会遇到电脑无法连接到手机情况,首先在cmd命令输入adb devices查看是否报错,报错绝大可能是5037端口被占用了,因为adb默认绑定的是5037端口 1.查看占用端口的进程PI ...
- LoRaWAN 1.1 网络协议规范 - 5 MAC指令
LoRaWAN 1.1 网络协议规范 LoRaWAN 1.1 版本封稿很久了也没有完整啃过一遍,最近边啃边翻译,趁着这个机会把它码下来. 如果觉得哪里有问题,欢迎留言斧正. 翻译不易,转载请申明出处和 ...
- [mongoDB]PyMongo Cursor Not Found Error
Python跑一个aggregate脚本,报错:pymongo.errors.CursorNotFound: Cursor not found, cursor id: 35411720832 搜了下原 ...
- 潭州课堂25班:Ph201805201 爬虫高级 第十课 Scrapy-redis分布 (课堂笔记)
利用 redis 数据库,做 request 队列,去重,多台数据共享, scrapy 调度 基于文件每户,默认只能在单机运行, scrapy-redis 默认把数据放到 redis 中,实现数据共享 ...
- vue中,class与style绑定
<template> <div> <p v-bind:class="{active:isActive,'demo':Demo}">嘿嘿</ ...
- IDEA 配置datasource,提升编码效率,让你在 Mapper.xml 中编写sql可以飞起来~
IDEA 2018 创建springboot工程后,如果你打开一个.sql文件,或者一个mybatis的mapper.xml文件,会提示: No data source are configured ...
- JavaScript踩坑
1 //这样做会抛出错误 alert(ttt); //这样做不会,只是会弹出undefine而已 alert(window.ttt); 当然可以try catch如此捕获异常 try { //这样做会 ...