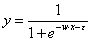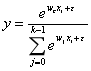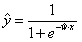机器学习---三种线性算法的比较(线性回归,感知机,逻辑回归)(Machine Learning Linear Regression Perceptron Logistic Regression Comparison)
最小二乘线性回归,感知机,逻辑回归的比较:
|
最小二乘线性回归 Least Squares Linear Regression |
感知机 Perceptron |
二分类逻辑回归 Binary Logistic Regression |
多分类逻辑回归 Multinomial Logistic Regression |
|
|
特征x |
x=([x1,x2,...,xn,1])T |
|||
|
权重w |
w=([w1,w2,...,wn,b])T |
|||
|
目标y |
实数(负无穷大到正无穷大) |
两个类别 1,-1 |
两个类别 0,1 |
多个类别 c=0,1,...,k-1 |
|
目标函数 |
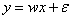 |
 |
(类别1的概率) |
for c=0,1,...,k-1 (全部类别的概率) |
|
对y的估计 |
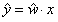 |
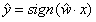 |
(类别1的概率) |
for c=0,1,...,k-1 (全部类别的概率) |
|
映射函数 |
无 |
sign函数 |
sigmoid函数 |
softmax函数 |
|
算法的作用 |
预测连续值(回归) |
预测离散值(分类) |
预测离散值(分类) |
预测离散值(分类) |
|
损失函数 |
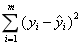 |
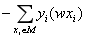 |
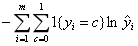 |
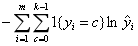 |
|
损失函数的含义 |
观测值与估计值之间的欧式距离平方和 |
错误分类点距离分类超平面的总长度 |
估计的概率分布与真实的概率分布之间的相似程度,对于样本(xi,yi),它的正确分类类别是c,那么如果它计算出的目标属于类别c的分类概率的值为1,则说明分类完全正确,这种情况下对损失函数没有贡献(ln1=0);而如果分类错误,则它计算出的目标属于类别c的的分类概率将是一个小于1的值,这种情况下将对损失函数有所贡献 |
估计的概率分布与真实的概率分布之间的相似程度,对于样本(xi,yi),它的正确分类类别是c,那么如果它计算出的目标属于类别c的分类概率的值为1,则说明分类完全正确,这种情况下对损失函数没有贡献(ln1=0);而如果分类错误,则它计算出的目标属于类别c的的分类概率将是一个小于1的值,这种情况下将对损失函数有所贡献 |
|
损失函数的本质 |
目标y的条件概率P(y|x)在高斯分布下的极大似然估计(取负数和对数) |
/ |
目标y的条件概率P(y|x)在伯努利分布下的极大似然估计(取负数和自然对数) |
目标y的条件概率P(y|x)在多项分布下的极大似然估计(取负数和自然对数) |
|
最优解方法 |
解析解(closed form),梯度下降法,牛顿法,拟牛顿法 |
随机梯度下降法,牛顿法,拟牛顿法 |
梯度下降法,牛顿法,拟牛顿法 |
梯度下降法,牛顿法,拟牛顿法 |
机器学习---三种线性算法的比较(线性回归,感知机,逻辑回归)(Machine Learning Linear Regression Perceptron Logistic Regression Comparison)的更多相关文章
- Stanford机器学习---第三讲. 逻辑回归和过拟合问题的解决 logistic Regression & Regularization
原文:http://blog.csdn.net/abcjennifer/article/details/7716281 本栏目(Machine learning)包括单参数的线性回归.多参数的线性回归 ...
- FIFO、LRU、OPT这三种置换算法的缺页次数
考虑下述页面走向: 1,2,3,4,2,1,5,6,2,1,2,3,7,6,3,2,1,2,3,6 当内存块数量分别为3时,试问FIFO.LRU.OPT这三种置换算法的缺页次数各是多少? 答:缺页定义 ...
- 排序—时间复杂度为O(n2)的三种排序算法
1 如何评价.分析一个排序算法? 很多语言.数据库都已经封装了关于排序算法的实现代码.所以我们学习排序算法目的更多的不是为了去实现这些代码,而是灵活的应用这些算法和解决更为复杂的问题,所以更重要的是学 ...
- 基于C#程序设计语言的三种组合算法
目录 基于C#程序设计语言的三种组合算法 1. 总体思路 1.1 前言 1.2 算法思路 1.3 算法需要注意的点 2. 三种组合算法 2.1 普通组合算法 2.2 与自身进行组合的组合算法 2.3 ...
- 网络中,FIFO、LRU、OPT这三种置换算法的缺页次数
FIFO.LRU.OPT这三种置换算法的缺页次数 转载 由于要考计算机四级网络,这里遇到了问题,就搜了一些资料来解疑. 考虑下述页面走向: 1,2,3,4,2,1,5,6,2,1,2,3,7,6,3 ...
- 三种Hash算法对比以及秒传原理.
三种Hash算法对比以及秒传原理 CRC (32/64) MD5 Sha1 分5个点来说 1.校验值长度 2.校验值类别 3.安全级别 4.应用场景 1).校验值长度 CRC(32/64) 分别 ...
- 机器学习---用python实现最小二乘线性回归算法并用随机梯度下降法求解 (Machine Learning Least Squares Linear Regression Application SGD)
在<机器学习---线性回归(Machine Learning Linear Regression)>一文中,我们主要介绍了最小二乘线性回归算法以及简单地介绍了梯度下降法.现在,让我们来实践 ...
- 创建B树,动态添加节点,并使用三种遍历算法对树进行遍历
ks17:algorithm apple$ cat btree_test.c ///********************************************************** ...
- Spark MLlib回归算法------线性回归、逻辑回归、SVM和ALS
Spark MLlib回归算法------线性回归.逻辑回归.SVM和ALS 1.线性回归: (1)模型的建立: 回归正则化方法(Lasso,Ridge和ElasticNet)在高维和数据集变量之间多 ...
随机推荐
- AutoCAD ObjectARX 二次开发(2020版)--3,执行ARX文件--
上一节中我们在initApp()函数中,将helloWorld()函数注册给了CAD主程序,注册指令的字符串为“Hello”. void initApp() { acedRegCmds->add ...
- np.minimum()与tf.minimum()的用法
总结:二者用法一致.a=np.array([[[[10,8,3,9],[5,6,7,8]]],[[[1,2,3,4],[5,6,7,8]]],[[[1,2,3,4],[5,6,7,8]]]] )pri ...
- 【开发笔记】- QQ消息轰炸
1.右键新建一个文本文件: 2.打开记事本将如下代码复制过去: On Error Resume Next Dim wsh,ye set wsh=createobject("wscript.s ...
- TypeScript编写Vue项目结构解析
使用TypeScript编写Vue项目也已经有了一段时间,笔者在刚刚使用TypeScript时候也是很茫然,不知道从何下手,感觉使用TypeScript写项目感觉很累赘并不像JavaScript那么灵 ...
- vue辅助函数mapStates与mapGetters
状态管理器 <!-- store.js: --> import Vue from 'vue' import Vuex from 'vuex' Vue.use(Vuex) export de ...
- 图说jdk1.8新特性(3)--- 注解与类型推测优化
获取同一类型多个注解 jdk1.8的java.lang.Class类新增了方法getAnnotationsByType方法,该方法可以获取某一个类型的注解列表,具体代码示例如下: public c ...
- maven学习笔记三(依赖特性,作用域)
上一章中 我们看到了添加了个junit的依赖包.那么maven中想添加依赖的jar包我们只需要配置相应的dependency就行.例如: <dependency> <groupId ...
- linux设备驱动程序-i2c(1):i2c总线的添加与实现
linux设备驱动程序-i2c(1):i2c总线的添加与实现 (基于4.14内核版本) 在上一章节linux设备驱动程序-i2c(0)-i2c设备驱动源码实现中,我们演示了i2c设备驱动程序的源码实现 ...
- 微信小程序转义解析渲染html
今天开发小程序时,想调用商品详情字段,发现大部分是用编辑器编辑的html原生标签,无法在小程序直接使用. 后面自己使用正则和字符串替换,效果也不佳. 最后在网上找到了wx-mina-html-view ...
- JVM——垃圾回收资格的判定
一:判断一个对象是否已死 1:引用数算法:给对象加个引用计数器,被引用时加一,引用失效减一,在任何时刻一直为0的就说明不会被使用,但是由于一种情况的存在,导致这种算法不被JVM所考虑,在两个对象相互引 ...