8皇后问题SQL求解（回溯算法）

问题

八皇后问题是一个古老而著名的问题，是回溯算法的典型例题。该问题是十九世纪著名的数学家高斯1850年提出：在8X8格的国际象棋上摆放八个皇后，使其不能互相攻击，即任意两个皇后都不能处于同一行、同一列或同一斜线上，问有多少种摆法

百度来的代码

回溯法用递归实现八皇后解法

declare
  type t_queen is varray(8) of number;
  queen t_queen := t_queen(1, 2, 3, 4, 5, 6, 7, 8);
  l_num number := 0;
  -- 显示“八皇后”
  procedure show(queen t_queen) is
  begin
    l_num := l_num + 1;
    dbms_output.put_line(rpad('---- NO. ' || l_num || ' ', 16, '-'));
    -- 从第1行显示到第8行
    for r in 1 .. 8 loop
      -- 当前行，从第1列显示到第8列
      for c in 1 .. 8 loop
        -- “皇后”用“Q”表示，空位用“.”表示
        dbms_output.put(case when queen(r) = c then 'Q' else '.'
                        end || ' ');
      end loop;
      dbms_output.put_line(null);
    end loop;
  end;
  -- 冲突检测。检测第row行与第1行至第row-1行是否冲突。
  -- 不冲突，返回true；冲突返回false
  function is_ok(queen t_queen, row number) return boolean is
    t number;
  begin
    for r in 1 .. row - 1 loop
      if queen(r) = queen(row) then
        -- 第row行与第r行的皇后在同一列上，冲突
        return false;
      end if;
      t := queen(r) - queen(row);
      if t = r - row or t = row - r then
        -- 第row行与第r行的皇后在同一斜线上，冲突
        return false;
      end if;
    end loop;
    return true;
  end;
  -- 递归查找所有排列
  procedure find(queen in out t_queen, row number) is
  begin
    for col in 1 .. 8 loop
      -- 每一行列的位置从第1列到第8列检测
      queen(row) := col;
      if is_ok(queen, row) then
        if row = 8 then
          -- 已经查找到第8行，查找结束，显示结果
          show(queen);
          return;
        end if;
        find(queen, row + 1); -- 尚未查找到第8行，第归查找一下行
      end if;
    end loop;
  end;
begin
  find(queen, 1); -- 从第1行开始查找
end;

运行结果

共92种结果

还有百度到了另外一种更简洁的写法

利用Oracle 11R2版本的递归属性，算法很简单，也就是在斜线上，直线上无冲突即可

with sou as (
     select level n,1 k from dual connect by  level<=8
),
     ntt(n,k) as (
     select sou.n ,sou.k  from sou where k=1
     union all
     select ntt.n*10+a.n
            ,ntt.k+1
     from ntt,sou a
     where not exists(select 1
                      from  (select level b1 from dual connect by level<=7) t
                      where t.b1<=ntt.k and (
                             a.n=to_number(substr(to_char(ntt.n),b1,1)) or
                             a.n=to_number(substr(to_char(ntt.n),b1,1))+(ntt.k+1-t.b1) or
                             a.n=to_number(substr(to_char(ntt.n),b1,1))-(ntt.k+1-t.b1)
                             )
                     ) and ntt.k<=7
     )
select n from ntt where ntt.k=8  ;

也是92种结果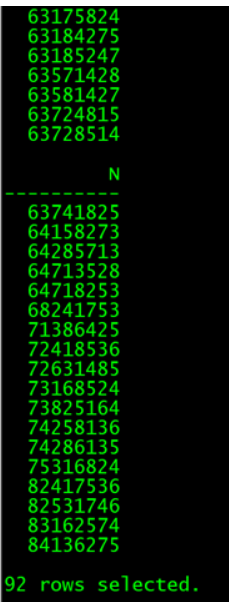

结果是一个数字表示在棋盘上的位置，也可以改一下用两位整数表示一个棋位，这样可以扩展到10皇后以上

时间因素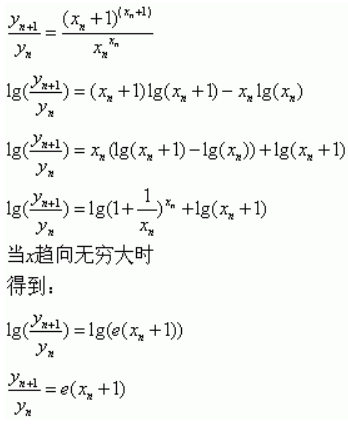：也即每增加一个皇后，增加的时间约为上一个的e(x+1)倍