BZOJ 1202 狡猾的商人 差分约束or带权并查集

题目链接：

https://www.lydsy.com/JudgeOnline/problem.php?id=1202

题目大意：

刁姹接到一个任务，为税务部门调查一位商人的账本，看看账本是不是伪造的。账本上记录了n个月以来的收入情况，其中第i 个月的收入额为Ai(i=1,2,3...n-1,n)， 。当 Ai大于0时表示这个月盈利Ai 元，当 Ai小于0时表示这个月亏损Ai 元。所谓一段时间内的总收入，就是这段时间内每个月的收入额的总和。 刁姹的任务是秘密进行的，为了调查商人的账本，她只好跑到商人那里打工。她趁商人不在时去偷看账本，可是她无法将账本偷出来，每次偷看账本时她都只能看某段时间内账本上记录的收入情况，并且她只能记住这段时间内的总收入。 现在，刁姹总共偷看了m次账本，当然也就记住了m段时间内的总收入，你的任务是根据记住的这些信息来判断账本是不是假的。

思路：

一：差分约束系统转化

对于一段区间的和，可以转化成前缀和相减的形式。

比如区间a-b的和为c，也就是sum[b] - sum[a - 1] = c

可以写成两个式子：

sum[b] - sum[a - 1] <= c

sum[b] - sum[a - 1] >= c

根据差分约束系统式子：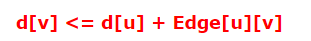

也就是a-1到b 权值为c

b到a-1 权值为-c

判断有没有负环，有的话无解，输出false。

二、带权并查集：

也是转化成前缀和的形式。对于每个节点所带的权值cnt[i] = s[root] - s[i]

1、如果x=a-1，y=b在同一子树中，cnt[x] = s[root] - s[x] cnt[y] = s[root] - s[y]

那么cnt[x] - cnt[y] = s[y] - s[x]判断是否等于输入值c。

2、不在同一子树，进行合并。

设fx为x子树根节点 fy为y子树根节点。

有cnt[x] = s[fx] - s[x] cnt[y] = s[fy] = s[y] 目前又给出条件：s[y] - s[x] = z;

将fy并入fx中，那么cnt[fy]应该设置成s[fx] - s[fy]

由上述三个式子可得：cnt[fy]应该设置成cnt[x] - cnt[y] - z

这样带权并查集的合并就写好了。

差分：

 #include<bits/stdc++.h>
 #define IOS ios::sync_with_stdio(false);//不可再使用scanf printf
 #define Max(a, b) ((a) > (b) ? (a) : (b))//禁用于函数，会超时
 #define Min(a, b) ((a) < (b) ? (a) : (b))
 #define Mem(a) memset(a, 0, sizeof(a))
 #define Dis(x, y, x1, y1) ((x - x1) * (x - x1) + (y - y1) * (y - y1))
 #define MID(l, r) ((l) + ((r) - (l)) / 2)
 #define lson ((o)<<1)
 #define rson ((o)<<1|1)
 #define Accepted 0
 #pragma comment(linker, "/STACK:102400000,102400000")//栈外挂
 using namespace std;
 inline int read()
 {
     int x=,f=;char ch=getchar();
     while (ch<''||ch>''){if (ch=='-') f=-;ch=getchar();}
     while (ch>=''&&ch<=''){x=x*+ch-'';ch=getchar();}
     return x*f;
 }

 typedef long long ll;
 const int maxn =  + ;
 const int MOD = ;//const引用更快，宏定义也更快
 const int INF = 1e9 + ;
 const double eps = 1e-;

 struct edge
 {
     int v, w;
     edge(){}
     edge(int v, int w):v(v), w(w){}
 };
 vector<edge>e;
 vector<int>G[maxn];
 bool inq[maxn];//是否在队列中
 int d[maxn];
 int cnt[maxn];//入队次数
 int n, m;
 void addedge(int u, int v, int w)
 {
     e.push_back(edge(v, w));
     G[u].push_back(e.size() - );
 }
 bool SPFA()
 {
     queue<int>q;
     memset(inq, , sizeof(inq));
     memset(cnt, , sizeof(cnt));
     for(int i = ; i <= n; i++){d[i] = ; inq[] = true;q.push(i);}
     while(!q.empty())
     {
         int u = q.front();
         q.pop();
         inq[u] = ;
         for(int i = ; i < G[u].size(); i++)
         {
             int v = e[G[u][i]].v;
             int w = e[G[u][i]].w;
             if(d[v] > d[u] + w)
             {
                 d[v] = d[u] + w;
                 if(!inq[v])
                 {
                     q.push(v);
                     inq[v] = ;
                     if(++cnt[v] > n)return true;
                 }
             }
         }
     }
     return false;
 }
 int main()
 {
     int T;
     scanf("%d", &T);
     while(T--)
     {
         scanf("%d%d", &n, &m);
         for(int i = ; i <= n; i++)G[i].clear();
         e.clear();
         int u, v, w;
         for(int i = ; i <= m; i++)
         {
             scanf("%d%d%d", &u, &v, &w);
             u--;
             addedge(u, v, w);
             addedge(v, u, -w);
         }
         if(SPFA())puts("false");
         else puts("true");
     }
     return Accepted;
 }

带权并查集：

 #include<bits/stdc++.h>
 #define IOS ios::sync_with_stdio(false);//不可再使用scanf printf
 #define Max(a, b) ((a) > (b) ? (a) : (b))//禁用于函数，会超时
 #define Min(a, b) ((a) < (b) ? (a) : (b))
 #define Mem(a) memset(a, 0, sizeof(a))
 #define Dis(x, y, x1, y1) ((x - x1) * (x - x1) + (y - y1) * (y - y1))
 #define MID(l, r) ((l) + ((r) - (l)) / 2)
 #define lson ((o)<<1)
 #define rson ((o)<<1|1)
 #define Accepted 0
 #pragma comment(linker, "/STACK:102400000,102400000")//栈外挂
 using namespace std;
 inline int read()
 {
     int x=,f=;char ch=getchar();
     while (ch<''||ch>''){if (ch=='-') f=-;ch=getchar();}
     while (ch>=''&&ch<=''){x=x*+ch-'';ch=getchar();}
     return x*f;
 }

 typedef long long ll;
 const int maxn =  + ;
 const int MOD = ;//const引用更快，宏定义也更快
 const int INF = 1e9 + ;
 const double eps = 1e-;

 int cnt[maxn];//cnt[i]表示s[root] - s[i]
 int p[maxn];
 int Find(int x)
 {
     if(x == p[x])return x;
     int tmp = Find(p[x]);//此处不可以先路径压缩，需要更新x之后再进行路径压缩
     cnt[x] += cnt[p[x]];//一开始 cnt[x] = s[p[x]] - s[x] cnt[p[x]] = s[root] - s[p[x]]
     p[x] = tmp;         //需要路径压缩转化成 cnt[x] = s[root] - s[x]
     return p[x];
 }
 int main()
 {
     int T;
     scanf("%d", &T);
     while(T--)
     {
         int n, m;
         scanf("%d%d", &n, &m);
         for(int i = ; i <= n; i++)p[i] = i, cnt[i] = ;
         int flag = ;
         for(int i = ; i <= m; i++)
         {
             int x, y, z;
             scanf("%d%d%d", &x, &y, &z);
             x--;
             int fx = Find(x), fy = Find(y);
             if(fx != fy)
             {
                 //目前已知 s[y] - s[x] = z  cnt[x] = s[fx] - s[x] cnt[y] = s[fy] - s[y]
                 //将y的根fy并入x的根fx中 那么需要设置cnt[fy] = s[fx] - s[fy]
                 //所以cnt[fy] = s[fx] - s[fy] = s[x] + cnt[x] - (s[y] + cnt[y]) = cnt[x] - cnt[y] - z
                 cnt[fy] = cnt[x] - cnt[y] - z;
                 p[fy] = fx;
             }
             else if(cnt[x] - cnt[y] != z)//验证s[y] - s[x] == z 等价于验证 cnt[x] - cnt[y] == z
             {
                 flag = ;
             }
         }
         if(flag)puts("false");
         else puts("true");
     }
     return Accepted;
 }