Tree - Gradient Boosting Machine with sklearn source code

This is the second post in Boosting algorithm. In the previous post, we go through the earliest Boosting algorithm - AdaBoost, which is actually an approximation of exponential loss via additive stage-forward modelling. What if we want to choose other loss function? Can we have a more generic algorithm that can apply to all loss function.

Gradient Descent

Friedman proposed another way to optimize the additive function- Gradient descent, same as the numerical optimization method used in neural network. Basically at each step we calculate the gradient against current additive function $F_m(x)$ to first find the direction of loss reduction and then a line search is used to find the step length.

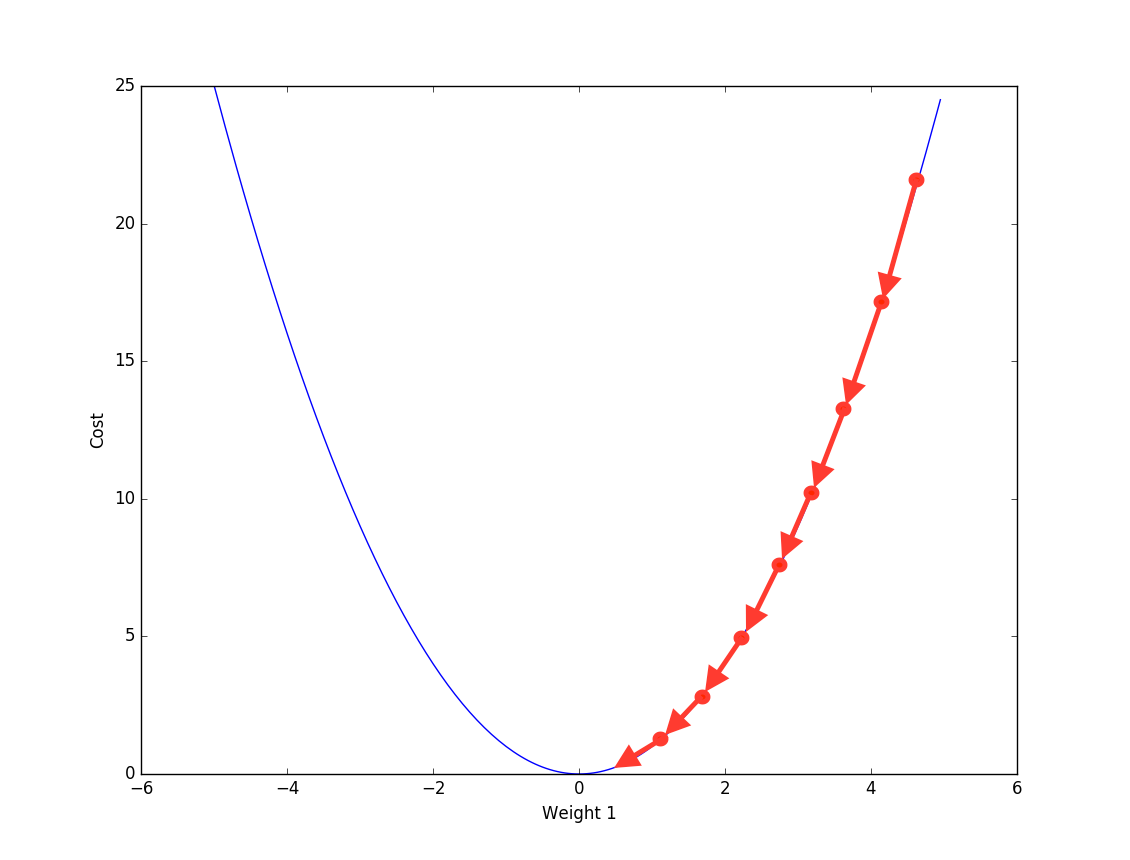
So far we have already mentioned 2 main components in Gradient Boosting machine:

Boosting: $F_m(x) = \sum \rho_m h(x;\alpha_m)$ final function is an additive model of multiple base learner.
Optimization: Gradient descent is used as numeric optimization method.

There is one other important component, which we will cover later.

Gradient Boosting Basic

Here is the generic frame work of gradient Boosting algorithm.

Algorithm 1: Gradient_Boost

$F_0(x) = argmin \sum_i^N{L(y_i,p)}$

For m = 1 to M do :

A. $\hat{y_i} = - {[\frac{\partial{L(y_i, F(x_i)) }}{\partial{F(x_i ) } } ] } $ $ \text{ where $F(x) = F_{m-1}(x)$} $

B. $a_m = argmin_{\alpha, \beta}\sum_i^N{[\hat{y_i} - \beta h(x_i;
\alpha)]^2}$

C. $\rho_m = argmin_{\rho}\sum_i^N{L(y_i, F_{m-1}(x_i) + \rho h(x_i; \alpha_m))}$

D. $ F_m(x_i) = F_{m-1}(x_i) + \rho h(x_i; \alpha_m))$

$F_m(x_i)$ will be final prediction

Let's go through all the above steps one by one.

Step1 we initialize the additive model, usually we can initialize with 0.

Then at each iteration:

A. Calculate negative gradient of current additive function

B. Fit a base learner to approximate negative gradient (direction of loss reduction).

C. find optimal coefficient for above base learner (step length), by minimizing the loss function.

D. update the additive function with new base learner and coefficient.

Step B is very important in the algorithm. Because given $x$ and current additive function $F_{m-1}(x)$, for each $x_i$ we will have a empirical gradient. However we don't want the model to over-fit the training data. That's why an approximation estimation is used. Above we use Least-squares-Loss to fit the base leaner to the negative gradient, because least-squares estimates conditional expectation - $E(\hat{y}|x)$

Next let's use 2 loss function as example:

Least-Squares, all steps follow above algorithm, and we can further specify 2(A) 2(B) 2(C) as following:

Algorithm 2: LS_Boost

$F_0(x) = argmin \sum_i^N{L(y_i,p)}$

For m = 1 to M do :

A. $\hat{y_i} = y_i - F(x_i) \text{ where $F(x) = F_{m-1}(x)$}$

B. $a_m = argmin_{\alpha, \beta}\sum_i^N{[\hat{y_i} - \beta h(x_i;\alpha)]^2}$

C. $\rho_m =\beta $

D. $ F_m(x_i) = F_{m-1}(x_i) + \rho h(x_i; \alpha_m))$

Here negative gradient is simply the current residual. Since we already use least-square regression to fit base learner to the residual, where we not only get the base learner but also the coefficient. Therefore step 2(c) is no longer needed.

Least-absolute-deviation, all steps follow above algorithm, and we can further specify 2(A) 2(B) 2(C) as following:

Algorithm 3: LAD_Boost

$F_0(x) = argmin \sum_i^N{L(y_i,p)}$

For m = 1 to M do :

A. $\hat{y_i} = sign( y_i - F(x_i) ) \text{ where $F(x) = F_{m-1}(x)$}$

B. $a_m = argmin_{\alpha, \beta}\sum_i^N{[\hat{y_i} - \beta h(x_i;\alpha)]^2}$

C.$\rho_m = argmin_{\rho}\sum_i^N{ |\hat{y_i} - \rho h(x_i; \alpha_m)|}$

D. $ F_m(x_i) = F_{m-1}(x_i) + \rho h(x_i; \alpha_m))$

Here negative gradient is the sign of residual. And as before we fit base learner to the sign via least-squares regression.

Boosting married Tree

Now is time to reveal the last component of Gradient Boosting Machine - using Regression Tree as base learner. Same as AdaBoost, Gradient Boosting have more attractive features when it uses regression tree as base learner.

Therefore we can further represent each base leaner as an additive model (we mentioned in the previous Decision Tree Post) like below

\[h(x_i; \{b_j, R_j\}_1^J) = \sum_{j=1}^J{b_j I(x \in R_j)}
\]

Instead of using linear regression, we fit a regression tree against negative gradient. With Least-square as loss function, $b_j$ will the be average of gradient in each leaf.

We can further simplify this by combining $b_j$ with coefficient $\rho_m$, as following:

\[\begin{align}
F_m(x_i) &= F_{m-1}(x_i) + \rho\sum_{j=1}^J{b_{jm} I(x \in R_{jm})}\\
F_m(x_i) &= F_{m-1}(x_i) + \sum_{j=1}^J{\lambda_{jm} I(x \in R_{jm})}
\end{align}
\]

The above transformation shows that when we fit the regression tree, we only need the node split, not the leaf assignment. In other words we are fitting Unit Gradient.

Later given the sample in each leaf, we calculate the leaf assignment by minimizing the loss function within each leaf. This will return the same result as minimizing the loss function over all sample, because all leaves are disjoint.

\[\lambda_{jm} = argmin \sum_{x \in R_{jm}}{L(y_i, F_{m-1}(x_i) + \lambda)}
\]

This is also why each base learner (tree) needs to be a weak leaner. If the tree is deep enough that each leaf has only 1 sample, then we are just calculating empirical gradient of the training data (over-fitting).

From here we will use tree as default base learner, and let's go through all kinds of loss functions supported by Sklearn.

Sklean source code - loss function

Sklearn supports 7 loss function in total, 3 for classification and 4 for regression, see below

Type	Loss	Estimator
ClassificationLossFunction	BinomialDeviance	LogOddsEstimator
ClassificationLossFunction	MultinomialDeviance	PriorProbabilityEstimator
ClassificationLossFunction	MultinomialDeviance	PriorProbabilityEstimator
RegressionLossFunction	LeastSquaresError	MeanEstimator
RegressionLossFunction	LeastAbsoluteError	QuantileEstimator
RegressionLossFunction	HuberLossFunction	QuantileEstimator
RegressionLossFunction	QuantileLossFunction	QuantileEstimator

Here the Estimator calculates the prediction given training sample, including average, quantile(median), probability of each classes, or log-odds ($\log p/1-p$).

Each loss classes supports several methods, including calculating loss, negative gradient and update terminal regions.

For update_terminal_regions method, it first assign each sample to a leaf, perform line search to get leaf assignment and then update the prediction accordingly, see below:

class LossFunction(six.with_metaclass(ABCMeta, object)):

	def update_terminal_regions(self, tree, X, y, residual, y_pred,

                                sample_weight, sample_mask,

                                learning_rate=1.0, k=0):

        terminal_regions = tree.apply(X)

        for leaf in np.where(tree.children_left == TREE_LEAF)[0]:

            self._update_terminal_region(tree, masked_terminal_regions,

                                         leaf, X, y, residual,

                                         y_pred[:, k], sample_weight)

        y_pred[:, k] += (learning_rate

                         * tree.value[:, 0, 0].take(terminal_regions, axis=0))

Next let's take a deeper dive into all loss functions.

Regression

1. Least-squares (LS)

Algorithm 4: LS_TreeBoost

$F_0(x) = mean(y_i)$

For m = 1 to M do :

A. $\hat{y_i} = y_i - F(x_i) \text{ where $F(x) = F_{m-1}(x)$}$

B. $\{R_{jm}\}_1^J = \text{J terminal node tree}(\{\hat{y_i}, x_i\}_1^N)$

C. $\lambda_{jm} = mean_{x_i \in R_{jm}}{ y_i - F(x_i)} $

D. $ F_m(x_i) = F_{m-1}(x_i) + \sum_{j=1}^J \lambda_{jm} I(x_i \in R_{jm})$

Compare algorithm 4 with algorithm 2, the difference lies in how the negative gradient is estimated, linear regression vs. regression tree. And how the coefficient is calculated, regression coefficient vs. sample mean in each leaf. And one attractive of LS is that it can get leaf assignment directly from gradient approximation. Therefore in the class update_terminal_regions is directly called to update prediction.

class LeastSquaresError(RegressionLossFunction):

    def init_estimator(self):

        return MeanEstimator()

    def __call__(self, y, pred, sample_weight=None):

		return np.mean((y - pred.ravel()) ** 2.0)

    def negative_gradient(self, y, pred, **kargs):

        return y - pred.ravel()

    def update_terminal_regions(self, tree, X, y, residual, y_pred, learning_rate=1.0, k=0):

        y_pred[:, k] += learning_rate * tree.predict(X).ravel()

2. Least-absolute-deviation (LAD)

Algorithm 5: LAD_TreeBoost

$F_0(x) = median(y_i)$

For m = 1 to M do :

A. $\hat{y_i} = sign( y_i - F(x_i) ) \text{ where $F(x) = F_{m-1}(x)$}$

B. $\{R_{jm}\}_1^J = \text{J terminal node tree}(\{\hat{y_i}, x_i\}_1^N)$

C. $\lambda_{jm} = median_{x_i \in R_{jm}}{ y_i - F(x_i)} $

D. $ F_m(x_i) = F_{m-1}(x_i) + \sum_{j=1}^J \lambda_{jm} I(x_i \in R_{jm})$

From algorithm implementation, we can see LAD is a very robust algorithm, which only use sample order to adjust the prediction accordingly. In _update_terminal_region, sample median in each leaf are used as leaf assignment.

class LeastAbsoluteError(RegressionLossFunction):

    def init_estimator(self):

        return QuantileEstimator(alpha=0.5)

    def __call__(self, y, pred, sample_weight=None):

		return np.abs(y - pred.ravel()).mean()

    def negative_gradient(self, y, pred, **kargs):

        pred = pred.ravel()

        return 2.0 * (y - pred > 0.0) - 1.0

    def _update_terminal_region(self, tree, terminal_regions, leaf, X, y, residual, pred, sample_weight):

        terminal_region = np.where(terminal_regions == leaf)[0]

        sample_weight = sample_weight.take(terminal_region, axis=0)

        diff = y.take(terminal_region, axis=0) - pred.take(terminal_region, axis=0)

        tree.value[leaf, 0, 0] = _weighted_percentile(diff, sample_weight, percentile=50)

3. Huber Loss (M-Regression)

Huber is between LS and LAD, which uses LS when the error is smaller than certain quantile and use LAD when the error exceeds certain quantile, see below:

\[\begin{align}
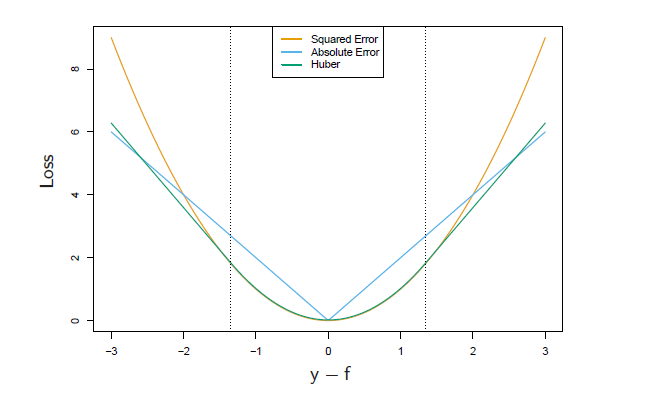
L(y,F) =
\begin{cases}
\frac{1}{2}(y-F)^2 & \quad & |y-F| \leq \delta \\
\delta(|y-F| - \delta/2) & \quad & |y-F| > \delta
\end{cases}
\end{align}
\]

where $\delta$ is usually a certain quantile of absolute error. In additive model, we will use current additive prediction to estimate this quantile.

\[\delta = quantile_{\alpha}(|y-F|)
\]

Then we can further calculate negative gradient, and use a regression tree to approximate it.

\[\begin{align}
\tilde{y} =\begin{cases}
y-F \quad & |y-F| \leq \delta \\
\delta \cdot sign(y-F) \quad & |y-F| > \delta
\end{cases}
\end{align}
\]

In the end we need to minimize loss in each leaf, which can be a little tricky with Huber loss function. For LAD, optimal leaf value is the median, for LS, optimal leaf value is the mean. For Huber an approximation method is used, where we use the sample within $\delta$ to adjust the overall median, like following:

\[\lambda_{jm}= \tilde{\gamma_{jm}} + \frac{1}{N_{jm}}\sum_{x \in R_{jm}} sign(\gamma_{m-1}(x_i) -\tilde{\gamma_{jm}} ) \cdot min(\delta_m, abs(\gamma_{m-1}(x_i) -\tilde{\gamma_{jm}}))
\]

where $\tilde{\gamma_{jm}} = median(\gamma_{jm}) = median(y-F)$ is the LAD estimation - median of residual in each leaf.

Algorithm 6: M_TreeBoost

$F_0(x) = median(y_i)$

For m = 1 to M do :

A. $r_{m-1} = y_i - F(x_i)$

B. $\delta_m = quantile_{\alpha}(|r_{m-1}|_1^N)$

C. $

\tilde{y} =\begin{cases}

y-F \quad & |y-F| \leq \delta_m \

\delta_m \cdot sign(y-F) \quad & |y-F| > \delta_m

\end{cases} $

D. $\{R_{jm}\}_1^J = \text{J terminal node tree}(\{\tilde{y}, x_i\}_1^N)$

E. $\lambda_{jm}= \tilde{\gamma_{jm}} + \frac{1}{N_{jm}}\sum_{x \in R_{jm}} sign(\gamma_{m-1}(x_i) -\tilde{\gamma_{jm}} ) \cdot min(\delta_m, abs(\gamma_{m-1}(x_i) -\tilde{\gamma_{jm}}))$

F. $ F_m(x_i) = F_{m-1}(x_i) + \sum_{j=1}^J \lambda_{jm} I(x_i \in R_{jm})$

In application, I found Huber-Loss to be a very powerful loss function. Because it is not that sensitive to the outlier, but is able to capture more information than just sample order as LAD.

class HuberLossFunction(RegressionLossFunction):

	def init_estimator(self):

        return QuantileEstimator(alpha=0.5)

    def __call__(self, y, pred, sample_weight=None):

        pred = pred.ravel()

        diff = y - pred

		gamma = stats.scoreatpercentile(np.abs(diff), self.alpha * 100)

        gamma_mask = np.abs(diff) <= gamma

		sq_loss = np.sum(0.5 * diff[gamma_mask] ** 2.0)

		lin_loss = np.sum(gamma * (np.abs(diff[~gamma_mask]) - gamma / 2.0))

		loss = (sq_loss + lin_loss) / y.shape[0]

        return loss

    def negative_gradient(self, y, pred, sample_weight=None, **kargs):

        pred = pred.ravel()

        diff = y - pred

		gamma = stats.scoreatpercentile(np.abs(diff), self.alpha * 100)

        gamma_mask = np.abs(diff) <= gamma

        residual = np.zeros((y.shape[0],), dtype=np.float64)

        residual[gamma_mask] = diff[gamma_mask]

        residual[~gamma_mask] = gamma * np.sign(diff[~gamma_mask])

        self.gamma = gamma

        return residual

    def _update_terminal_region(self, tree, terminal_regions, leaf, X, y,

                                residual, pred, sample_weight):

        terminal_region = np.where(terminal_regions == leaf)[0]

        sample_weight = sample_weight.take(terminal_region, axis=0)

        gamma = self.gamma

        diff = (y.take(terminal_region, axis=0)

                - pred.take(terminal_region, axis=0))

        median = _weighted_percentile(diff, sample_weight, percentile=50)

        diff_minus_median = diff - median

        tree.value[leaf, 0] = median + np.mean(

            np.sign(diff_minus_median) *

            np.minimum(np.abs(diff_minus_median), gamma))

Classification

1. 2-class classification

For binomial classification, our calculation below will be slightly different from Freud's paper. Because Sklearn use $y \in \{0,1\}$, while in Freud's paper $y \in \{-1,1\}$ is used. Of course, whichever you use, you should get the same result. You need to make sure that your calculation is consistent. Relevant bug was spotted in Sklearn before.

Do you still recall how is the binomial log-likelihood defined? We define current prediction as log-odds.

\[\begin{align}
F & = \log(\frac{P(y=1|x)}{P(y=0|x)}) \\
P &= \frac{1}{1+e^{-F}} \\
\end{align}
\]

And use above to calculate negative log-likelihood function, we get following

\[\begin{align}
L(y,F) & = - E(y\log{p} + (1-y)log{(1-p)} ) \\
& = - E( y\log{\frac{p}{1-p}} + \log({1-p}) ) \\
& = - E( yF - \log{(1+e^F)} )
\end{align}
\]

The negative gradient is below, I also give a general version, which is in line with later k-class regression

\[\begin{align}
\tilde{y} & = y - \frac{1}{1+ e^{-,F}} = y - \sigma(F) = y - p
\end{align}
\]

In the end we calculate leaf assignment by minimizing the loss in each leaf

\[\lambda_{jm} = argmin \sum_{x \in R_{jm}} - E( yF - \log{(1+e^F)} )
\]

There is no close solution to above function, a second-order Newton Raphson is used to approximate

Quick Note - Newton Raphson

$f(x + \epsilon) \approx f(x) + f'(x)\epsilon + \frac{1}{2}f''(x)\epsilon^2$ 2nd order Taylor expansion

To get optimal value, $f'(x) = 0$

we will get $\epsilon = -\frac{f'(x)}{f''(x)}$

\[\begin{align}
\lambda_{jm} & = \sum_{x \in R_{jm}}(y - \frac{1}{1+ e^{-F}} )/(\frac{1}{1+ e^{-F}} \cdot \frac{1}{1+ e^{F}}) \\
& = \sum_{x \in R_{jm}} \tilde{y} / ( (y-\tilde{y}) \cdot (1-y+\tilde{y}) )
\end{align}
\]

Algorithm 7: L2_TreeBoost

$F_0(x) = 0$

For m = 1 to M do :

A. $\tilde{y} = y - \frac{1}{1+ e^{-F}} \text{ where $F(x) = F_{m-1}(x)$}$

B. $\{R_{jm}\}_1^J = \text{J terminal node tree}(\{\hat{y_i}, x_i\}_1^N)$

C. $\lambda_{jm} = \sum_{x \in R_{jm}} \tilde{y} / ( (y-\tilde{y}) \cdot (1-y+\tilde{y})) $

D. $ F_m(x_i) = F_{m-1}(x_i) + \sum_{j=1}^J \lambda_{jm} I(x_i \in R_{jm})$

class BinomialDeviance(ClassificationLossFunction):

	def init_estimator(self):

        return LogOddsEstimator()

    def __call__(self, y, pred, sample_weight=None):

        pred = pred.ravel()

		return -2.0 * np.mean((y * pred) - np.logaddexp(0.0, pred)) #logaddexp(0, v) == log(1.0 + exp(v))

    def negative_gradient(self, y, pred, **kargs):

        return y - expit(pred.ravel()) # sigmoid function 

    def _update_terminal_region(self, tree, terminal_regions, leaf, X, y,

                                residual, pred, sample_weight):

        terminal_region = np.where(terminal_regions == leaf)[0]

        residual = residual.take(terminal_region, axis=0)

        y = y.take(terminal_region, axis=0)

        sample_weight = sample_weight.take(terminal_region, axis=0)

        numerator = np.sum(sample_weight * residual)

        denominator = np.sum(sample_weight * (y - residual) * (1 - y + residual))

		tree.value[leaf, 0, 0] = numerator / denominator

2. k-class classification

Loss function is defined in the same ways with multiclass:

\[L(y,F) = -\sum_{k=1}^K y_k \log p_k(x)
\]

where $p_k(x) = exp(F_k(x))/\sum_{l=1}^Kexp(F_l(x))$

Therefore we will get the loss function nad negative gradient as following:

\[\begin{align}
L(y,F) &= -\sum_{k=1}^K y_kF_k(x) - log(\sum_{l=1}^Kexp(F_l(x)))\\
\tilde{y_i} &= y_{ki} - p_{k,m-1}(x_i)
\end{align}
\]

Algorithm 8: LK_TreeBoost

$F_0(x) = 0$

For m = 1 to M do :

A. $p_k(x) = exp(F_k(x))/\sum_{l=1}^Kexp(F_l(x))$

B. $\tilde{y_i} = y_i - p_k(x_i)$

B. $\{R_{jm}\}_1^J = \text{J terminal node tree}(\{\hat{y_i}, x_i\}_1^N)$

C. $\lambda_{jm} = \sum_{x \in R_{jm}} \tilde{y} / ( (y-\tilde{y}) \cdot (1-y+\tilde{y})) $

D. $ F_m(x_i) = F_{m-1}(x_i) + \sum_{j=1}^J \lambda_{jm} I(x_i \in R_{jm})$

sklearn source code - GBM Framework

Base Learner

Base learner in each iteration is trained via fit_stage method. A Decision Tree is trained to approximate negative gradient given current additive function. And then leaf assignment is calculated to minimize loss function in each leaf.

def _fit_stage(self, i, X, y, y_pred, sample_weight, sample_mask, random_state, X_idx_sorted, X_csc=None, X_csr=None):

	assert sample_mask.dtype == np.bool

	loss = self.loss_

	original_y = y

	for k in range(loss.K):

		residual = loss.negative_gradient(y, y_pred, k=k, sample_weight=sample_weight)

		tree = DecisionTreeRegressor(

			criterion=self.criterion,

			splitter='best',

			max_depth=self.max_depth,

			min_samples_split=self.min_samples_split,

			min_samples_leaf=self.min_samples_leaf,

			min_weight_fraction_leaf=self.min_weight_fraction_leaf,

			min_impurity_decrease=self.min_impurity_decrease,

			min_impurity_split=self.min_impurity_split,

			max_features=self.max_features,

			max_leaf_nodes=self.max_leaf_nodes,

			random_state=random_state,

			presort=self.presort)

		tree.fit(X, residual, sample_weight=sample_weight,

				 check_input=False, X_idx_sorted=X_idx_sorted)

		loss.update_terminal_regions(tree.tree_, X, y, residual, y_pred,sample_weight, sample_mask, self.learning_rate, k=k)

		self.estimators_[i, k] = tree

	return y_pred

Boosting

Boosting is performed upon above base learner via fit_stages method. In each iteration a new base learner is trained given current additive function.

n_estimators specifies the number of iteration (# of base learner).

subsample indicates the split between training sample and validation sample. Base learner is trained against training sample, and we use untouched validation sample for performance.

def _fit_stages(self, X, y, y_pred, sample_weight, random_state,

				begin_at_stage=0, monitor=None, X_idx_sorted=None):

    n_samples = X.shape[0]

	do_oob = self.subsample < 1.0

	sample_mask = np.ones((n_samples, ), dtype=np.bool)

	n_inbag = max(1, int(self.subsample * n_samples))

	loss_ = self.loss_

	i = begin_at_stage

	for i in range(begin_at_stage, self.n_estimators):

		if do_oob:

			sample_mask = _random_sample_mask(n_samples, n_inbag,

											  random_state)

			old_oob_score = loss_(y[~sample_mask],

								  y_pred[~sample_mask],

								  sample_weight[~sample_mask])

		y_pred = self._fit_stage(i, X, y, y_pred, sample_weight, sample_mask, random_state, X_idx_sorted, X_csc, X_csr)

		if do_oob:

			self.train_score_[i] = loss_(y[sample_mask],

										 y_pred[sample_mask], sample_weight[sample_mask])

			self.oob_improvement_[i] = (

				old_oob_score - loss_(y[~sample_mask],

									  y_pred[~sample_mask], sample_weight[~sample_mask]))

	return i + 1

Reference

J. Friedman, Greedy Function Approximation: A Gradient Boosting Machine, The Annals of Statistics, Vol. 29, No. 5, 2001.
J. Friedman, Stochastic Gradient Boosting, 1999
T. Hastie, R. Tibshirani and J. Friedman. Elements of Statistical Learning Ed. 2, Springer, 2009.
Bishop, Pattern Recognition and Machine Learning 2006
scikit-learn tutorial http://scikit-learn.org/stable/modules/generated/sklearn.ensemble.GradientBoostingClassifier.html