HDU 3103 Shoring Up the Levees(计算几何 搜寻区域)

主题链接：http://acm.hdu.edu.cn/showproblem.php?pid=3103

Problem Description

The tiny country of Waterlogged is protected by a series of levees that form a quadrilateral as shown below:










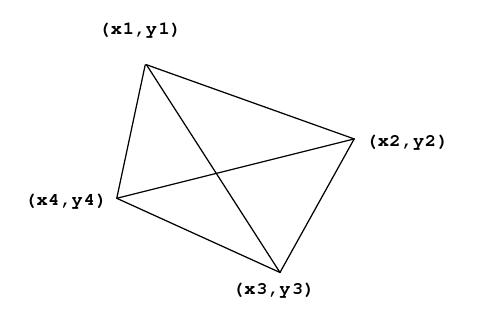
The quadrilateral is defined by four vertices. The levees partition the country into four quadrants. Each quadrant is identified by a pair of vertices representing the outside edge of that quadrant. For example, Quadrant 1 shown below is defined by the points
(x1, y1) and (x2, y2) .










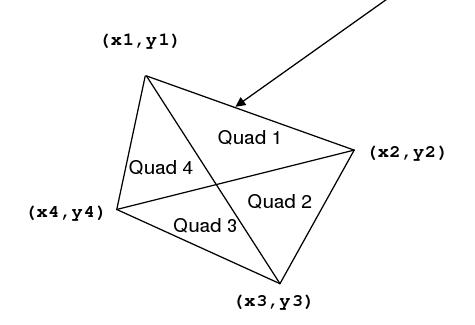
It happens very often that the country of Waterlogged becomes flooded, and the levees need to be reinforced, but their country is poor and they have limited resources. They would like to be able to reinforce those levees that encompass the largest area first,
then the next largest second, then the next largest third, and the smallest area fourth.



Help Waterlogged identify which quadrants are the largest, and the length of the levees around them.

 

Input

here will be several sets of input. Each set will consist of eight real numbers, on a single line. Those numbers will represent, in order:





X1 Y1 X2 Y2 X3 Y3 X4 Y4





The four points are guaranteed to form a convex quadrilateral when taken in order -- that is, there will be no concavities, and no lines crossing. Every number will be in the range from -1000.0 to 1000.0 inclusive. No Quadrant will have an area or a perimeter
smaller than 0.001. End of the input will be a line with eight 0.0's.

 

Output

For each input set, print a single line with eight floating point numbers. These represent the areas and perimeters of the four Quadrants, like this:





A1 P1 A2 P2 A3 P3 A4 P4





Print them in order from largest area to smallest -- so A1 is the largest area. If two Quadrants have the same area when rounded to 3 decimal places, output the one with the largest perimeter first. Print all values with 3 decimal places of precision (rounded).
Print spaces between numbers. Do not print any blank lines between outputs.

 

Sample Input

1 2 1 5 5 2 2 0
3.5 2.2 4.8 -9.6 -1.2 -4.4 -8.9 12.4
0.0 0.0 0.0 0.0 0.0 0.0 0.0 0.0

 

Sample Output

5.100 11.459 3.400 9.045 0.900 6.659 0.600 4.876
44.548 38.972 21.982 25.997 20.342 38.374 10.038 19.043

 

Source

2008 ACM-ICPC Southeast USA Regional

题意：

给出四个点，连接对角线后，分为四个象限。依照面积大小依次输出，假设面积同样则依照周长大小输出（注意：比較面积是否同样是比較保留了三位后是否同样）；

代码例如以下：

#include<stdio.h>
#include<string.h>
#include<math.h>
#include<algorithm>
using namespace std;
const double eps = 1e-5;
const double PI = acos(-1.0);

struct point
{
    double x, y;
};
struct gao
{
    double mz,zc;
};
struct gao gg[10];

bool cmp(gao a,gao b)
{
    if(a.mz!=b.mz)
        return a.mz>b.mz;
    return a.zc>b.zc;
}
double xmult(double x1,double y1,double x2,double y2,double x0,double y0)
{
    return (x1-x0)*(y2-y0)-(x2-x0)*(y1-y0);
}

//判两点在线段同側,点在线段上返回0
int same_side(point p1,point p2,point l1,point l2)
{
    return xmult(l1.x,l1.y,p1.x,p1.y,l2.x,l2.y)*xmult(l1.x,l1.y,p2.x,p2.y,l2.x,l2.y)>0;
}

//两点距离
double dis(point a,point b)
{
    return sqrt((a.x-b.x)*(a.x-b.x)+(a.y-b.y)*(a.y-b.y));
}
//两线段的交点
point intersection(point u1,point u2,point v1,point v2)
{
    point ret=u1;
    double t=((u1.x-v1.x)*(v1.y-v2.y)-(u1.y-v1.y)*(v1.x-v2.x))
             /((u1.x-u2.x)*(v1.y-v2.y)-(u1.y-u2.y)*(v1.x-v2.x));
    ret.x+=(u2.x-u1.x)*t;
    ret.y+=(u2.y-u1.y)*t;
    return ret;
}

//三点面积
double aera(point a,point b,point c)
{
    double aa,bb,cc,q;
    aa=dis(c,b);
    bb=dis(a,c);
    cc=dis(b,a);
    q=(aa+bb+cc)/2;
    double h=sqrt(q*(q-aa)*(q-bb)*(q-cc));
    h=(int)(h*1000+0.5);
    return h*0.001;
}

//三点周长
double get_zc(point a,point b,point c)
{
    double aa,bb,cc,q;
    aa=dis(c,b);
    bb=dis(a,c);
    cc=dis(b,a);
    q=(aa+bb+cc);
    return q;
}

int main()
{
    int i;
    double x1,y1,x2,y2,x3,y3,x4,y4;
    point a,b,c,d,e;
    while(scanf("%lf%lf%lf%lf%lf%lf%lf%lf",&x1,&y1,&x2,&y2,&x3,&y3,&x4,&y4)!=EOF)
    {
        if(x1==0 && y1==0 && x2==0 && y2==0 && x3==0 && y3==0 && x4==0 && y4==0)
            break;
        a.x=x1;
        a.y=y1;
        b.x=x2;
        b.y=y2;
        c.x=x3;
        c.y=y3;
        d.x=x4;
        d.y=y4;
        if(same_side(a, b, c,d)==0)
            e = intersection(d,c,a,b);
        else if(same_side(d, b, c, a)==0)
            e = intersection(d,b,c,a);
        else
            e = intersection(b,c,d,a);
        gg[0].mz=aera(a,b,e);
        gg[1].mz=aera(b,c,e);
        gg[2].mz=aera(c,d,e);
        gg[3].mz=aera(a,d,e);
        gg[0].zc=get_zc(a,b,e);
        gg[1].zc=get_zc(b,c,e);
        gg[2].zc=get_zc(c,d,e);
        gg[3].zc=get_zc(a,d,e);
        sort(gg,gg+4,cmp);
        for(i=0; i<3; i++)
            printf("%.3lf %.3lf ",gg[i].mz,gg[i].zc);
        printf("%.3lf %.3lf\n",gg[i].mz,gg[i].zc);
    }
    return 0;
}
/*
2 0 2 2 0 2 0 0
*/

版权声明：本文博主原创文章，博客，未经同意不得转载。