并不对劲的bzoj2638

为了反驳很对劲的太刀流，并不对劲的片手流决定与之针锋相对。

很对劲的太刀流->

2638: 黑白染色

Time Limit: 20 Sec Memory Limit: 256 MB
Submit: 177 Solved: 87
[Submit][Status][Discuss]

Description

　你有一个n*m的矩形，一开始所有格子都是白色，然后给出一个目标状态的矩形，有的地方是白色，有的地方是黑色，你每次可以选择一个连通块（四连通块，且不要求颜色一样）进行染色操作（染成白色或者黑色）。问最少操作次数。

Input

　　第一行两个数n，m表示矩形大小。
　　接下来n行描述目标状态，每行m个字符，’W’表示白色，’B’表示黑色。

Output

　　一行一个整数表示操作数。

Sample Input

3 3
WBW
BWB
WBW

Sample Output

HINT

数据规模和约定
　　100%的数据n<=50,m<=50
　　15%的数据n*m<=15
　　另外15%的数据m=1

——————————并不对劲的分界线——————

问：数据怎样？

答：极小！

问：极小的数据该怎么办？

答：网络流！神奇的dp！

然而并不是…有一个游戏(KAMI)是类似的，就是给出这样的一个有几种颜色的图：

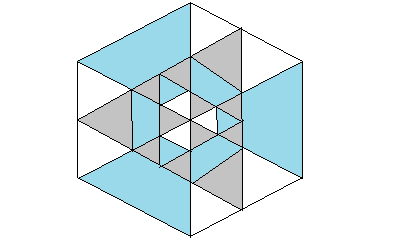
每次可以选一个同色的区域，将这个区域染成另一种颜色。要在步数限制内将整个图染成同一种颜色。

有这样一种染色方法：

用三步将中间的部分染灰；

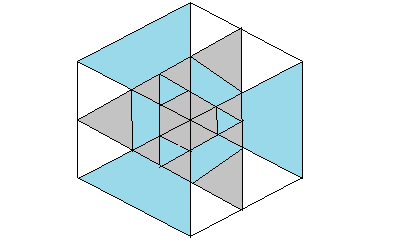
用一步将中间的部分染蓝；

用一步将中间的部分染灰；

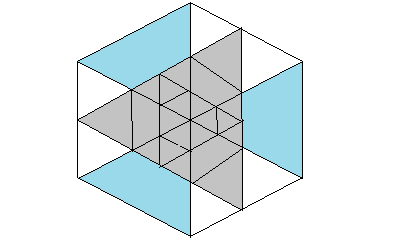
用一步将中间的部分染蓝；

用一步将中间的部分染白，就完成了；

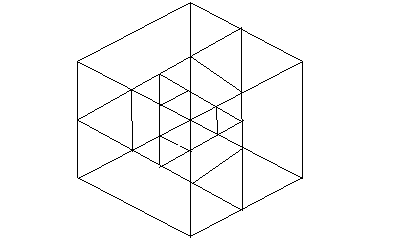
总共是3+1+1+1+1=7步，并不知道这是不是最优解。

这个游戏和这道题的区别在于有一个是把有图案的变成空白，另一个是把空白的变成有图案的。会发现这个游戏的操作正好是本题操作的逆变换。因为本游戏一开始是小的同色连通块，染色后是更大的同色连通块（必须是白色）。对于本题而言，如果把有不同颜色的连通块染成了同一颜色，就会让之前的某些操作白做了。这可能不会让总次数变多，但是绝对不可能让总次数变少，所以还是要尽量避免将不同色的染成同色的。那也就是说，这道题就是将大的白色联通块变成小的同色连通块，刚好相反。那么就可以直接将本题当成那个游戏的简化版（只有两种颜色），也就是将目标状态染成全白。

这个游戏的有一种策略就是选一个起点（不同的起点的结果当然不同了，所以要先在选起点上花一番心思），然后将起点所在的同色连通块染成它的边缘的颜色（因为只有两种颜色，所以并不用考虑边缘有多种颜色的情况）。不断重复直至所有点同色。有人可能觉得，将一些小的连通块不断合并次数会更少。考虑两点A，B，将“从黑走到白”或“从白走到黑”称为一步，A到B最少的步数为dis(A,B)。那么无论如何染色，A和B只能在至少dis(A,B)次后才能在同一个同色连通块。所以其实这两种策略的下界都一样，但是第一种更容易考虑。

随便找一个点（黑白都行）作为起点，假设它的颜色为a，另一种颜色为b。每一次需要把起点所在的连通块染为b色，这样起点所在连通块边缘的那些颜色为b的点就都包含在连通块中了。再将起点所在的连通块染成a色，边缘的那些颜色为a的点就也包含再连通块中了。随便用bfs或者什么最短路算法就可以知道对于每个点，假如以该点为起点，那么一共需要多少步。最后再求个最小值。

还有一点，要是写最短路的话，总共有2500个点，floyd并不能过。但是会发现边数非常小，那么n遍dijkstra就行了。

#include<iostream>

#include<iomanip>

#include<cstdio>

#include<cstring>

#include<cstdlib>

#include<cmath>

#include<algorithm>

#include<queue>

#define maxn 3020

using namespace std;

inline int read()

{

    int x=0,f=1;

    char ch=getchar();

    while(isdigit(ch)==0 && ch!='-')ch=getchar();

    if(ch=='-')f=-1,ch=getchar();

    while(isdigit(ch))x=x*10+ch-'0',ch=getchar();

    return x*f;

}

inline void write(int x)

{

    int f=0;char ch[20];

    if(!x){puts("0");return;}

    if(x<0){putchar('-');x=-x;}

    while(x)ch[++f]=x%10+'0',x/=10;

    while(f)putchar(ch[f--]);

    putchar('\n');

}

typedef struct node

{

    int x,y;

    bool operator <(const node &z)const

    {

        return(y>z.y);

    }

}stnd;

priority_queue<stnd>q;

int dis[maxn],n,m,a,b,x[10]={1,0,-1,0},y[10]={0,1,0,-1},vis[maxn],maxt,ans=0x7fffffff;

char s[60][60];

int getn(int i,int j)

{

    return (i-1)*m+j;

}

void getxy(int w,int &i,int &j)

{

    j=w%m==0?m:w%m;

    i=(w-j)/m+1;

}

void dij(int st)

{

    memset(dis,-1,sizeof(dis));

    memset(vis,0,sizeof(vis));

    dis[st]=0;

    stnd tmp;tmp.x=st,tmp.y=0;

    q.push(tmp);

    while(!q.empty())

    {

        int u=q.top().x;q.pop();if(vis[u])continue;vis[u]=1;

        for(int r=0;r<4;r++)

        {

        	int i,j;getxy(u,i,j);

            int k=i+x[r],l=j+y[r],v=getn(k,l),w=s[i][j]==s[k][l]?0:1;

            //if(st==n*n)cout<<i<<" "<<j<<endl;

            if(k<=0 || k>n || l<=0 || l>m)continue;

            if(dis[v]>dis[u]+w || dis[v]==-1)

            {

            	dis[v]=dis[u]+w;

            	if(!vis[v]){tmp.x=v,tmp.y=dis[v],q.push(tmp);}

            }

        }

    }

    maxt=0;

    for(int i=1;i<=n*m;i++)

    {

    	int xx,yy;getxy(i,xx,yy);

    	if(s[xx][yy]=='B')

		{/*cout<<xx<<" "<<yy<<" "<<dis[i]<<endl;*/maxt=max(maxt,dis[i]);}

    }//cout<<maxt<<"+++++++++++"<<endl;

	ans=min(maxt,ans);

}

int main()

{

    n=read(),m=read();

    for(int i=1;i<=n;i++)

        scanf("%s",s[i]+1);

    for(int i=1;i<=n*m;i++)dij(i);

    write(ans+1);

    return 0;

}

/*

3 3

WBW

BWB

WBW

*/

/*

%%%Wang God orz

%%%Shing God orz

%%%Yangtze River God orz

%%%Bang God orz

%%%Cross God orz

%%%O God orz

%%%Destinies God orz

%%%Everyone Except Me

*/

不知道这一题会不会有多种颜色的强化版？如果有，假设共有k种颜色，那么能做到多少的数据范围？还是只能暴搜？

宣传一波电教，欢迎加入。