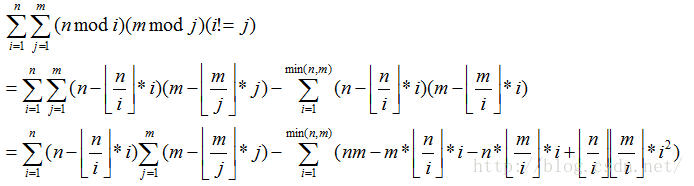BZOJ 1968_P1403 [AHOI2005]约数研究--p2260bzoj2956-模积和∑----信息学中的数论分块
第一部分
P1403 [AHOI2005]约数研究
题目描述
科学家们在Samuel星球上的探险得到了丰富的能源储备,这使得空间站中大型计算机“Samuel II”的长时间运算成为了可能。由于在去年一年的辛苦工作取得了不错的成绩,小联被允许用“Samuel II”进行数学研究。
小联最近在研究和约数有关的问题,他统计每个正数N的约数的个数,并以f(N)来表示。例如12的约数有1、2、3、4、6、12。因此f(12)=6。下表给出了一些f(N)的取值:

f(n)表示n的约数个数,现在给出n,要求求出f(1)到f(n)的总和。
输入输出格式
输入格式:
输入一行,一个整数n
输出格式:
输出一个整数,表示总和
输入输出样例
说明
【数据范围】
20%N<=5000
100%N<=1000000
200%N<=100000000000000
1000%N<=1000000000000000000000000000000000000000000000000000000000000000(63 0's)
本题原来基本上是一个暴力
不过结论比较重要
就是∑(i=1,n)d(i)=∑(i=1,n)(n/i)
此处下取整
这样的话发现对于比如说6
求右半部分为
6 3 2 1 1 1
有三个一
这重复计算了
这样可以实现二百分算法就是数论分块、
直接贴代码就行
#include<cstdio>
#include<iostream>
int n,ans=;
int main(){
scanf("%d",&n);
for(int i=,j;i<=n;i=j+){
j=n/(n/i);
ans+=(n/i)*(j-i+);
}
printf("%d",ans);
return ;
}
代码是对的!!!!!
1000分的算法需要反演等 达到n的三分之一次方logn
----------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------
模积和
所求就是第一行
n《=1e9;
图片是用的别人的叫qingdaobaibai,谢谢!!!
这样就分块显然了
预备知识:
1.前面的那个题的内容
2.欧拉定理
3.(费马小)
4.乘法逆元
5.阿尔贝恒等式的一些知识
∑aibi=∑(k:1,n)∑(i:1,k)ai(bk-bk+1)+sabn
这里列举一下纲目 将在另一个合适的博客里写
∑ai∑bi=∑∑aibj
等
这是代码
#include<iostream>
#include<cstdio>
#define ll long long
#define p 19940417
#define ine2 9970209
#define ine6 3323403
using namespace std;
ll n,m;
ll calc(ll k,ll n)
{
ll tmp=;
for (ll i=,pos=;i<=k;i=pos+)
{
pos=min(n/(n/i),k);
(tmp+=(n/i)%p*(((pos+)*(pos)%p*ine2%p-(i-)*i%p*ine2%p+p)%p)%p)%=p;
}
return (tmp+p)%p;
}
ll calc0(ll n,ll m)
{
ll tmp=;
for (ll i=,pos=;i<=n;i=pos+)
{
pos=min(n/(n/i),m/(m/i));
(tmp+=(n/i)*(m/i)%p*((pos*(pos+)%p*(pos*+)%p*ine6%p-(i-)*i%p*(i*-)%p*ine6%p+p)%p)%p)%=p;
}
return (tmp+p)%p;
}
int main()
{
scanf("%lld%lld",&n,&m);
if (n>m) swap(n,m);
ll t1=calc(n,n),t2=calc(m,m),t3=calc(n,m),t4=calc0(n,m);
ll ans=((((ll)n*n%p-t1+p)%p)*(((ll)m*m%p-t2+p)%p)%p-((ll)n*n%p*m%p-(ll)t1*m%p-(ll)t3*n%p+t4%p+p*)%p+p)%p;
cout << ans << endl;
return ;
}
代码本非我打,感谢原出处的教学。
这样的话基本数论分块的两种模式就显然了
BZOJ 1968_P1403 [AHOI2005]约数研究--p2260bzoj2956-模积和∑----信息学中的数论分块的更多相关文章
- 洛谷P2260 [清华集训2012]模积和(容斥+数论分块)
题意 https://www.luogu.com.cn/problem/P2260 思路 具体思路见下图: 注意这个模数不是质数,不能用快速幂来求逆元,要用扩展gcd. 代码 #include< ...
- 洛谷——P1403 [AHOI2005]约数研究
P1403 [AHOI2005]约数研究 题目描述 科学家们在Samuel星球上的探险得到了丰富的能源储备,这使得空间站中大型计算机“Samuel II”的长时间运算成为了可能.由于在去年一年的辛苦工 ...
- 洛谷P1403 [AHOI2005] 约数研究 [数论分块]
题目传送门 约数研究 题目描述 科学家们在Samuel星球上的探险得到了丰富的能源储备,这使得空间站中大型计算机“Samuel II”的长时间运算成为了可能.由于在去年一年的辛苦工作取得了不错的成绩, ...
- [AHOI2005]约数研究
题目描述 科学家们在Samuel星球上的探险得到了丰富的能源储备,这使得空间站中大型计算机“Samuel II”的长时间运算成为了可能.由于在去年一年的辛苦工作取得了不错的成绩,小联被允许用“Samu ...
- P1403 [AHOI2005]约数研究
原题链接 https://www.luogu.org/problemnew/show/P1403 这个好难啊,求约数和一般的套路就是求1--n所有的约数再一一求和,求约数又要用for循环来判断.... ...
- P1403 [AHOI2005]约数研究 题解
转载luogu某位神犇的题解QAQ 这题重点在于一个公式: f(i)=n/i 至于公式是怎么推出来的,看我解释: 1-n的因子个数,可以看成共含有2因子的数的个数+含有3因子的数的个数……+含有n因子 ...
- BZOJ1968 [Ahoi2005] 约数研究
Description Input 只有一行一个整数 N(0 < N < 1000000). Output 只有一行输出,为整数M,即f(1)到f(N)的累加和. Sample Input ...
- 1968. [AHOI2005]约数研究【数论】
Description Input 只有一行一个整数 N(0 < N < 1000000). Output 只有一行输出,为整数M,即f(1)到f(N)的累加和. Sample Input ...
- [luoguP1403] [AHOI2005]约数研究(这。。。)
传送门 用类似筛法的原理,就好啦 ——代码 #include <cstdio> int n, ans; int a[1000001]; int main() { int i, j; sca ...
随机推荐
- 51nod1126【矩阵快速幂】
思路: 自己的一点心得:中间矩阵为最终矩阵. 搞出来很简单的: #include <bits/stdc++.h> using namespace std; const int N=1e2+ ...
- PTA 模拟,【放着一定要写哈哈哈哈哈】(据说用string哟)
实现一种简单原始的文件相似度计算,即以两文件的公共词汇占总词汇的比例来定义相似度.为简化问题,这里不考虑中文(因为分词太难了),只考虑长度不小于3.且不超过10的英文单词,长度超过10的只考虑前10个 ...
- HDOJ4857【拓扑排序】
首先 CLJ ORZ 这道题做了两次,第一次瞎搞... 第二次,好吧,骄傲地说水过... 题意:不说了: 思路: 题目默认是小的在前面,那么就是反向建图,每次排序拿大的出来: 第一次做的时候,我记得我 ...
- Adore
(非公共题目) 问题描述 小 w 偶然间⻅到了一个 DAG.这个 DAG 有 m 层,第一层只有一个源点,最后一层只有一个汇点,剩下的每一层都有 k 个节点. 现在小 w 每次可以取反第 i(1 &l ...
- Win10各个版本免费激活密钥
专业版:W269N-WFGWX-YVC9B-4J6C9-T83GX 企业版:NPPR9-FWDCX-D2C8J-H872K-2YT43 家庭版:TX9XD-98N7V-6WMQ6-BX7FG-H8 ...
- mysql-SQL语法
细节查询:http://www.w3school.com.cn/sql/index.asp 1 DDL-data difinition lanuage数据定义语句 使我们有能力创建或删除表格,我们也可 ...
- Eclipse Neon Java版本安装Java EE插件
Help→Install New Software 地址:Neon - http://download.eclipse.org/releases/neon/201703231000 选择 Web,X ...
- iOS中数据类型转换--遇到则记录
1.NSString转NSNumber 使用情景:CoreData存储数据,其中一个为价格,CoreData里面定义为float 用文本输入框得到的数据类型是NSString,将NSString转换成 ...
- 转 PHP scandir() 函数
实例 列出 images 目录中的文件和目录: <?php $dir = "/images/"; // 以升序排序 - 默认 $a = scandir($dir); // 以 ...
- windows 7 正确禁用 IPv6
与Windows XP和Windows Server 2003不同的是,Windows Vista和Windows Server 2008中的IPv6无法被卸载.然而,在Windows Vista和W ...