外排序 & 败者树 & 多路归并-学习

来来来，根据这篇文章，学一下败者树吧：

http://blog.csdn.net/whz_zb/article/details/7425152

一、胜者树

胜者树的一个优点是，如果一个选手的值改变了，可以很容易地修改这棵胜者树。只需要沿着从该结点到根结点的路径修改这棵二叉树，而不必改变其他比赛的结果。

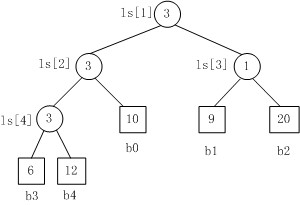
二、败者树

败者树是胜者树的一种变体。在败者树中，用父结点记录其左右子结点进行比赛的败者，而让胜者参加下一轮的比赛。败者树的根结点记录的是败者，需要加一个结点来记录整个比赛的胜利者。采用败者树可以简化重构的过程。

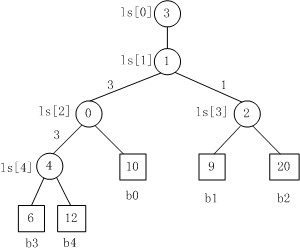
败者树 多路平衡归并外部排序

一 外部排序的基本思路

假设有一个72KB的文件，其中存储了18K个整数，磁盘中物理块的大小为4KB，将文件分成18组，每组刚好4KB。

首先通过18次内部排序，把18组数据排好序，得到初始的18个归并段R1~R18，每个归并段有1024个整数。

然后对这18个归并段使用4路平衡归并排序。

第1次归并：产生5个归并段
R11   R12    R13    R14    R15
其中
R11是由{R1,R2,R3,R4}中的数据合并而来
R12是由{R5,R6,R7,R8}中的数据合并而来
R13是由{R9,R10,R11,R12}中的数据合并而来
R14是由{R13,R14,R15,R16}中的数据合并而来
R15是由{R17,R18}中的数据合并而来
把这5个归并段的数据写入5个文件。

类推，下略。

二 使用败者树加快合并排序

外部排序最耗时间的操作时磁盘读写，对于有m个初始归并段，k路平衡的归并排序，磁盘读写次数为

|logkm|，可见增大k的值可以减少磁盘读写的次数，但增大k的值也会带来负面效应，即进行k路合并

的时候会增加算法复杂度。

如果使用败者树，可以在O(logk)的复杂度下得到最小的数，算法复杂度将为O((n-1)*logk)， 对于外部排序这种数据量超大的排序来说，这是一个不小的提高。