tarjan求割边割点

tarjan求割边割点

内容及代码来自http://m.blog.csdn.net/article/details?id=51984469

割边：在连通图中，删除了连通图的某条边后，图不再连通。这样的边被称为割边，也叫做桥。
割点：在连通图中，删除了连通图的某个点以及与这个点相连的边后，图不再连通。这样的点被称为割点。
DFS搜索树：用DFS对图进行遍历时，按照遍历次序的不同，我们可以得到一棵DFS搜索树。

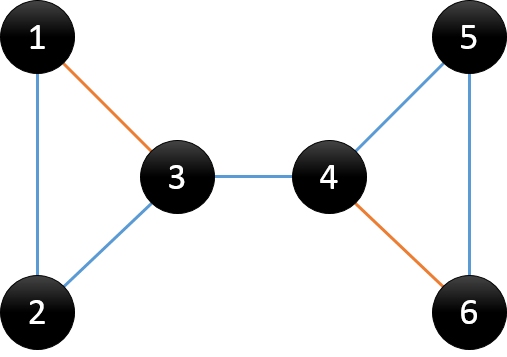
树边：在搜索树中的蓝色线所示，可理解为在DFS过程中访问未访问节点时所经过的边，也称为父子边
回边：在搜索树中的橙色线所示，可理解为在DFS过程中遇到已访问节点时所经过的边，也称为返祖边、后向边
观察DFS搜索树，我们可以发现有两类节点可以成为割点。对根节点u，若其有两棵或两棵以上的子树，则该根结点u为割点；对非叶子节点u(非根节点)，若其中的某棵子树的节点均没有指向u的祖先节点的回边，说明删除u之后，根结点与该棵子树的节点不再连通；则节点u为割点。对于根结点，显然很好处理；但是对于非叶子节点，怎么去判断有没有回边是一个值得深思的问题。我们用dfn[u]记录节点u在DFS过程中被遍历到的次序号，low[u]记录节点u或u的子树通过非父子边追溯到最早的祖先节点(即DFS次序号最小)，那么low[u]的计算过程如下。

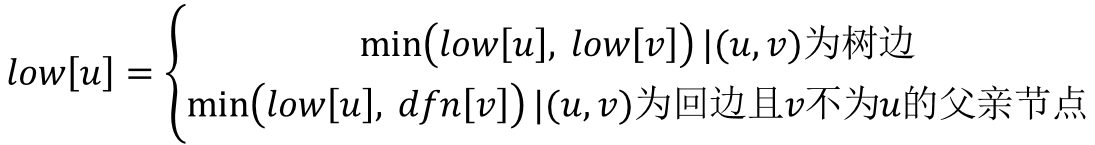
对于给的例子，其求出的dfn和low数组如下。
id     123456
dfn   123456
low   111444
可以发现，对于情况2，当(u,v)为树边且low[v]≥dfn[u]时，节点u才为割点。而当(u,v)为树边且low[v]>dfn[u]时，表示v节点只能通过该边(u,v)与u连通，那么(u,v)即为割边。tarjan算法的时间复杂度是O(n+m)的，非常快。
以hihoCoder1183为例给出代码：

 #include<cstdio>
 #include<vector>
 #include<algorithm>
 using namespace std;
 int n,m,order=;
 int low[],dfn[],father[],son[];
 //father:父结点 son:子结点个数
 vector<int> cutpoint,edge[];
 vector< pair<int,int> > cutedge;
 
 void tarjan(int u)
 {
     dfn[u]=low[u]=++order;
     bool flag=false;
     for (int i=;i<edge[u].size();i++)
     {
         int v=edge[u][i];
         if(!dfn[v])
         {
             son[u]++;
             father[v]=u;
              tarjan(v);
             if(low[v]>=dfn[u]) flag=true;
             //点u为割点
             if(low[v]>dfn[u]) cutedge.push_back(make_pair(min(v,u),max(v,u)));
             //边v-u为割边
             low[u]=min(low[u],low[v]);
         }
         else if(v!=father[u]) low[u]=min(low[u],dfn[v]);
     }
     //根节点若有两棵或两棵以上的子树则该为割点
     //非根节点若所有子树节点均没有指向u的祖先节点的回边则为割点
     if((father[u]==&&son[u]>)||(father[u]&&flag)) cutpoint.push_back(u);
 }
 
 int main()
 {
     scanf("%d%d",&n,&m);
     for (int i=;i<=m;i++)
     {
         int u,v;
         scanf("%d%d",&u,&v);
         edge[u].push_back(v),edge[v].push_back(u);
     }
     tarjan();
     sort(cutedge.begin(),cutedge.end());
     sort(cutpoint.begin(),cutpoint.end());
     if(==cutpoint.size()) puts("Null");
     else
     {
         printf("%d",cutpoint[]);
         for (int i=;i<cutpoint.size();i++) printf(" %d",cutpoint[i]);
         puts("");
     }
     for(int i=;i<cutedge.size();i++) printf("%d %d\n",cutedge[i].first,cutedge[i].second);
 }

不过话说一整篇博客，光复制别人的东西不大好，那我就上一个自己打的链表实现的代码：

 #include<cstdio>
 #include<vector>
 #include<algorithm>
 #define N 420000
 using namespace std;
 vector<int>cutpoint;
 vector<pair<int,int> >cutedge;
 int next[N],to[N],num,head[N],dfn[N],low[N],tim,son[N],father[N],n,m,a,b;
 bool flag;
 void add(int false_from,int false_to){
     next[++num]=head[false_from];
     to[num]=false_to;
     head[false_from]=num;
 }
 void dfs(int x){
     dfn[x]=low[x]=++tim;
     bool flag=;
     for(int i=head[x];i;i=next[i]){
         if(!dfn[to[i]]){
             son[x]++;
             father[to[i]]=x;
             dfs(to[i]);
             if(low[to[i]]>=dfn[x])
                 flag=;
             if(low[to[i]]>dfn[x])
                 cutedge.push_back(make_pair(min(x,to[i]),max(x,to[i])));
             low[x]=min(low[x],low[to[i]]);
         }
         else
             if(father[x]!=to[i])
                 low[x]=min(low[x],dfn[to[i]]);
     }
     if((!father[x]&&son[x]>)||(father[x]&&flag))
         cutpoint.push_back(x);
 }
 int main(){
     scanf("%d%d",&n,&m);
     for(int i=;i<=m;++i){
         scanf("%d%d",&a,&b);
         add(a,b);
         add(b,a);
     }
     dfs();
     sort(cutpoint.begin(),cutpoint.end());
     sort(cutedge.begin(),cutedge.end());
     printf("%d",cutpoint[]);
     for(int i=;i<cutpoint.size();i++)
         printf(" %d",cutpoint[i]);
     printf("\n");
     for(int i=;i<cutedge.size();i++)
         printf("%d %d\n",cutedge[i].first,cutedge[i].second);
     return ;
 }