算法导论 第十三章 红黑树（python）-1插入

红黑树是上一章二叉搜索树的改进，实现一种平衡 ，保证不会出现二叉树变链表的情况，基本动态集合操作的时间复杂度为O(lgn)

实际用途：c++stl中的set，map是用他实现的

红黑树的性质：

1.每个结点或是红色的，或是黑色的

2.跟结点是黑色的

3.每个叶结点（NIL）是黑色

4.如果一个结点是红色的，则它的两个结点都是黑色的

5.对每个结点，从该结点到其所有后代叶结点的简单路径上，均包含相同的数目的黑色结点（数目被称为黑高bh(x)）

如下图：

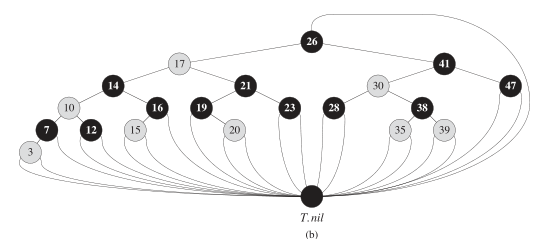
（T.nil 哨兵后面被忽略 None）

红黑树是二叉搜索树的改进，为了保证树的相对平衡，主要的不同就是增加了颜色这一属性，而后以颜色为起点的5条性质，为实现这5条性质我们要旋转和改色（插入，删除时）。

结点代码：

class Node: #红黑树结点类

    def __init__(self,data):
        self.left = None
        self.right = None
        self.parent = None
        self.data = data
        self.color = 'red' #初始化为red不是black看第5条黑高变化不好调节而red要好些

红黑树的旋转：保证平衡的一个关键

通过旋转在插入/删除时保持红黑树的5条性质-》保持树的相对平衡

这是基本的转换过程

主要调节 x和β ( β代码用B代替) x.parent和y  x和y之间的关系

代码过程：

   def left_rotate(self,root):
        '''
        围绕self转
        root根结点

        '''
        x = self
        #y必须存在
        y = x.right
        if y == None:
            return ;
        B = y.left
        #x 和 B
        x.right = B
        if B != None:
            B.parent = x

        #y和x.parent
        y.parent = x.parent
        if x.parent == None:
            #x为root结点
            root = y
        elif x == x.parent.left:
            x.parent.left = y
        else:
            x.parent.right = y

        #x和y
        y.left = x
        x.parent = y

    def right_rotate(self,root):
        '''
        围绕self转
        root根结点

        '''
        y = self
        #x必须存在
        x = y.left
        if x == None:
            return ;
        B = x.right
        #y 和 B
        y.left = B
        if B != None:
            B.parent = y

        #x和y.parent
        x.parent = y.parent
        if y.parent == None:
            #y为root结点
            root = x
        elif y == y.parent.left:
            y.parent.left = x
        else:
            y.parent.right = x

        #x和y
        x.right = y
        y.parent = x

红黑树插入：

我想先写一下我们插入的前提：

1.我们要保证红黑树的5点性质（将使用旋转变色保持-->保证达到先对平衡的关键）

2.我们默认插入的是红点--(破坏第2,4)对比插入黑点（破坏5）黑高的变化要求的是每个结点 更难满足

3.我们插入的位置都在叶子结点的位置（可以回忆一下二叉搜索树的代码）

插入的前一部分代码:(在二叉搜索树上的修改)

 def tree_insert(self,data):
        #插入data
        node = self
        while node:
            if data < node.data:
                next = node.left
            else:
                next = node.right
            if next:
                node = next
            else:
                break
        nn = self.createNode(data) #nn初始化颜色为red
        if data < node.data: #注data为根节点 不能不使用这个函数
            node.left = nn
            node.left.parent = node
        else:
            node.right = nn
            node.right.parent = node

        #我没有使用哨兵
        #变化
        nn.re_insert_fixup(self)#旋转变色保持性质
        return nn

画出所有的可能：#带有z的为插入位置

if 没有父亲结点（是root）： #在RBTree中直接改成黑色

graph graphname{ //图
z
z[color = red,style = filled]; //图中点的属性
}

 

昨天：找了一个用dit语言画图的一款软件GVEdit（360软件管家里有，官网好像被墙了？？使用边学习边使用）我参考的网址：http://blog.csdn.net/zhangskd/article/details/8250470

elif 有父亲结点：

    if 父亲结点为黑色：

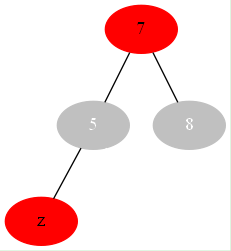或

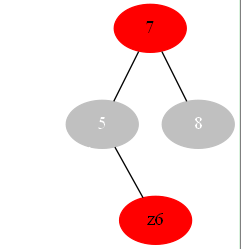
graph graphname{
7--5--z;//z我们插入的点
5--NULL[color = white]; //我使用了NULL写为白色伪装了一下，使图看起来更像二叉树 暂定的解决方法
7--8;
7,z[color = red,style = filled];
5,8[color = gray,style = filled,fontcolor = white];//使用灰色代替黑色 黑色显示太重
NULL[color = white,fontcolor=white]
}

     显然父亲结点为为黑对树的五个性质没有影响{注：关于第3条我默认是省略了叶子结点叶子结点是黑色}

    elif 父亲结点为红色：//到这才开始书上的伪代码

            if 父亲在祖父的左边

                   if 叔父为红色：#8为红色 书上情况1 #这里省略了一般部分 叔父就在右边下面的8

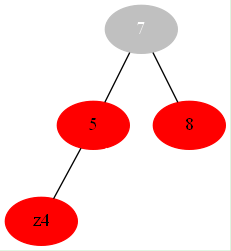或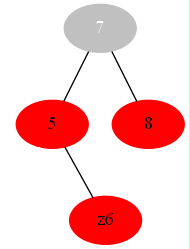

         #省去dot代码篇幅太长不好复习，也只是在上面的代码改的就不再谈了   

          看到这我老是在想可不可能转一下，但是根据4是不可能的，所以我们的选择是换色

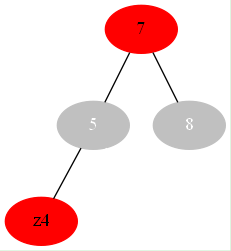或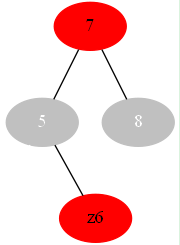

        显然黑高没变，如果7结点是root 直接改成黑色，如果不是应该递归处理//7变色了所以要处理一下

              if 结点 z->p->p == root

                    把其变黑

               else

  z = z->p->p#z在这里上移了 因为上面的7变色了

                    重新开始

         elif 叔父为黑色：

                if z 在父亲的右边： case2

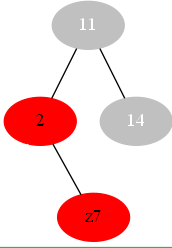-----变化为---->

                        #z是表示我们在代码中要变化的位置 #这图画的不好    偷懒了- -、

                        #显然情况变成了case3

                        #为什么要么换？？没想清

                elif z在父亲的左边： case3

----变为--->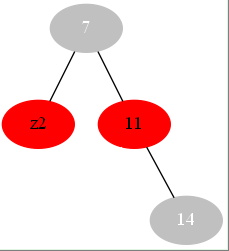

                        显然现在符合条

else：z的父亲在祖父的左边：对称的情况

画了怎么多思路还是有点乱我将条件判断拿出来，从整体上看一下。#和书上的代码可能不同 他省略了很多

if 没有父亲结点（是root）：

elif 有父亲结点：

    if 父亲结点为黑色：

    elif 父亲结点为红色：

    if 父亲在祖父的左边 #如果是红必有父结点

        if 叔父为红色:#case1

            #z在父亲的左边和右边都没有变化

            if 结点 z->p->p == root:

            else: 递归重新处理

        elif 叔父为黑色：情况2 + 3

            if z在父亲的右边：case2

            elif z在父亲的左边：case3

    elif 父亲在祖父的左边

   

  def re_insert_fixup(self,root):
        #插入时调节平衡部分
        z = self

        while z.parent != None and z.parent.color == 'red': #如果有父亲结点且他为红色
            if z.parent == z.parent.parent.left:
                y = z.parent.parent.right   #y是z的叔父
                if y.color == 'red':        #case 1
                    z.parent.color = 'black'
                    y.color = 'black'
                    z.parent.parent.color = 'red'
                    z = z.parent.parent
                else:
                    if z == z.parent.right: #case 2 --->case3
                        z = z.parent
                        z.right_rotate(root)
                    z.parent.color = 'black'
                    z.parent.parent.color = 'red'
                    z.parent.parent.right_rotate(root)
            else:
                y = z.parent.parent.left   #y是z的叔父
                if y.color == 'red':        #case 1
                    z.parent.color = 'black'
                    y.color = 'black'
                    z.parent.parent = 'red'
                    z = z.parent.parent
                else:
                    if z == z.parent.left: #case 2 --->case3
                        z = z.parent
                        z.left_rotate(root)
                    z.parent.color = 'black'
                    z.parent.parent.color = 'red'
                    z.parent.parent.left_rotate(root)

        root.color = 'black'

参考引用：

http://blog.csdn.net/fxjtoday/article/details/6448083

http://www.wutianqi.com/?p=2449

http://blog.csdn.net/zhangskd/article/details/8250470