[Luogu] P4460 [CQOI2018]解锁屏幕

题目背景

使用过Android 手机的同学一定对手势解锁屏幕不陌生。Android 的解锁屏幕由3X3 个点组成，手指在屏幕上画一条线，将其中一些点连接起来，即可构成一个解锁图案。如下面三个例子所示:

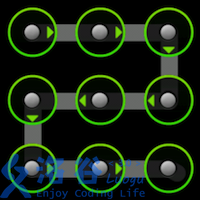
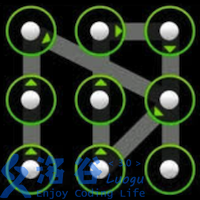
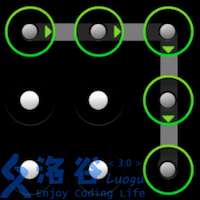
题目描述

画线时还需要遵循一些规则:

1. 连接的点数不能少于4 个。也就是说只连接两个点或者三个点会提示错误。

2. 两个点之间的连线不能弯曲。

3. 每个点只能“使用”一次，不可重复。这里的“使用”是指手指划过一个点，该点变绿。

4. 两个点之间的连线不能“跨过”另一个点，除非那个点之前已经被“使用”过了。

对于最后一条规则，参见下图的解释。左边两幅图违反了该规则; 而右边两幅图(分别为2->4-1-3-6 和6->5-4->1->9-2) 则没有违反规则，因为在“跨过”点时，点已经被“使用”过了。

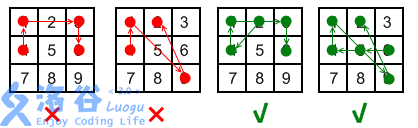
现在工程师希望改进解锁屏幕，增减点的数目，并移动点的位置，不再是一个九宫格形状，但保持上述画线的规则不变。请计算新的解锁屏幕上，一共有多少满足规则的画线方案。

题目解析

易证，Hsz是巨神。

状压dp，把每个点的状态记录下来，然后转移的时候注意处理4条规则。

复杂度很紧，注意常数

Code

我有个大胆的想法

#include<bits/stdc++.h>
using namespace std;const int mod = ;
int n,ans,dp[][<<],mid[][],X[],Y[];
inline bool judge(int a,int b,int c) {
    short xa=X[a],ya=Y[a],xb=X[b],yb=Y[b],xc=X[c],yc=Y[c];
    if((max(xa,xb)>=xc&&min(xa,xb)<=xc&&max(ya,yb)>=yc&&min(ya,yb)<=yc))
    return (float)(xa-xb)/(ya-yb)==(float)(xa-xc)/(ya-yc);return false;}
int main(register unsigned long long __locate,register unsigned long long __loc) {
    scanf("%d",&n);for(register int i=;i<n;i++) {scanf("%d%d",&X[i],&Y[i]);dp[i+][<<i]=;}
    for(int i=;i<n;i++) for(int j=;j<n;j++) if(i^j) for(int k=;k<n;k++) if((i^k)&&(j^k)) mid[i][j]|=judge(i,j,k)<<k;
    for(int i=;i<(<<n);i++) for(int j=;j<n;j++) if((<<j)&i) for(int k=;k<n;k++) if(!((<<k)&i))
    if((i&mid[j][k])==mid[j][k]) {dp[k+][i|(<<k)]+=dp[j+][i];if(dp[k+][i|(<<k)]>=mod) dp[k+][i|(<<k)]-=mod;}
    for(int i=;i<<<n;i++) if(__builtin_popcount(i)>=) for(int j=;j<=n;j++) {if((<<j-)&i) ans+=dp[j][i];
    if(ans>=mod)ans-=mod;} printf("%d",ans);return ;
}