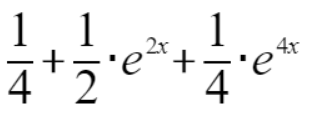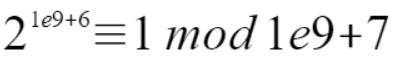SARS病毒 (生成函数 + 快速幂)
链接:https://ac.nowcoder.com/acm/contest/992/A
来源:牛客网
题目描述
目前,SARS 病毒的研究在世界范围内进行,经科学家研究发现,该病毒及其变种的 DNA 的一条单链中,胞嘧啶、腺嘧啶均是成对出现的。这虽然是一个重大发现,但还不是该病毒的最主要特征,因为这个特征实在太弱了。
为了进一步搞清楚该病毒的特征,CN 疾病控制中心和阿里巴巴集团合作,用科技的力量和程序的思维来解决这个难题。现阿里巴巴特委派你成为 CN 疾病控制中心的 SARS 高级研究员,去研究在这个特征下,可能成为 SARS 病毒的 DNA 序列的个数。更精确地说,你需要统计所有满足下列条件的长度为 n 的字符串的个数:
- 字符串仅由 A、T、C、G 组成
- A 出现偶数次(也可以不出现)
- C 出现偶数次(也可以不出现)
当 n=2 时,所有满足条件的字符串有如下 6个:
TT,TG,GT,GG,AA,CC。
注: 由于这个数可能非常庞大,你只需给出对 10^9+7 取模的结果即可。
输入描述:
- 多组输入(不超过10组),每行一个整数n:0 < n < 10^10^5
输出描述:
- 对于输入文件中的每一个 n,输出满足条件的字符串的个数对 10^9 +7 取模的结果。
输入
- 1
- 2
- 100
输出
- 2
- 6
- 113046907
- 析:首先这个一个生成函数的题目,从ACGT中可以知道,AC只能出现偶数次,而GT可以奇数,可以偶数,那么列出的生成函数是
前面那个是AC的,后面那个是GT的,这样列出来之后,就只要算出
这一项的系数就是答案了。
首先这个直接求是肯定求不出来的,要使用泰勒展式来求。
根据上面两个式子,可以对生成函数进行化简,化简后的结果就是
再根据泰勒展式,求出
该项的系数。
最终的结果就是,结果看起来很简单啊,但是 n 实在是太大了啊,所以还需要对 n 进行处理。
假设求 2n 这个结果,首先是要对 1e9 + 7 进行取模的,根据欧拉定理(其中 a 和 p 互质),根据本题来说那就是
所以 2n %1e9+7就可以进行变形成,变成这样,那么指数就是肯定小于1e9 + 7 了,那么就可以使用快速幂来计算了。
代码如下:
- #include <bits/stdc++.h>
- using namespace std;
- const long long mod = 1e9 + 7;
- inline long long fast_pow(long long a, int n){
- long long res = 1L;
- while(n){
- if(n&1) res = res * a % mod;
- n >>= 1;
- a = a * a % mod;
- }
- return res;
- }
- int main(){
- string s;
- while(cin >> s){
- long long ans = 0;
- for(int i = 0; i < s.size(); ++i)
- ans = (ans * 10 + s[i] - '0') % (mod - 1);
- ans = (ans - 2 + mod) % (mod - 1);
- cout << (fast_pow(2, ans) + fast_pow(4, ans)) % mod << endl;
- }
- return 0;
- }
SARS病毒 (生成函数 + 快速幂)的更多相关文章
- HDU 2065 "红色病毒"问题 ——快速幂 生成函数
$A(x)=1+x^2/2!+x^4/4!...$ $A(x)=1+x^1/1!+x^2/2!...$ 然后把生成函数弄出来. 暴力手算. 发现结论. 直接是$4^{n-1}+2^{n-1}$ 然后快 ...
- Bzoj4818:生成函数 快速幂
转来的题面:首先这题显然补集转化,就是用全部方案减去不含任何质数的方案.然后怎么做呢?考虑m比较小,我们能大力把<=m的质数全都筛出来.发现n很大,要么倍增要么快速幂......发现p相当小,所 ...
- hdu 2065 "红色病毒"问题(快速幂求模)
n=1 --> ans = 2 = 1*2 = 2^0(2^0+1) n=2 --> ans = 6 = 2*3 = 2^1(2^1+1) n=3 --> ans = 20 ...
- BZOJ4818 [SDOI2017]序列计数 【生成函数 + 快速幂】
题目 Alice想要得到一个长度为n的序列,序列中的数都是不超过m的正整数,而且这n个数的和是p的倍数.Alice还希望 ,这n个数中,至少有一个数是质数.Alice想知道,有多少个序列满足她的要求. ...
- 【指数型母函数+非递归快速幂】【HDU2065】"红色病毒"问题
大一上学完数分上后终于可以搞懂指数型母函数了.. 需要一点关于泰勒级数的高数知识 题目在此: "红色病毒"问题 Time Limit: 1000/1000 MS (Java/Oth ...
- 【XSY2612】Comb Avoiding Trees 生成函数 多项式求逆 矩阵快速幂
题目大意 本题的满二叉树定义为:不存在只有一个儿子的节点的二叉树. 定义一棵满二叉树\(A\)包含满二叉树\(B\)当且经当\(A\)可以通过下列三种操作变成\(B\): 把一个节点的两个儿子同时删掉 ...
- 2018.12.31 bzoj3992: [SDOI2015]序列统计(生成函数+ntt+快速幂)
传送门 生成函数简单题. 题意:给出一个集合A={a1,a2,...as}A=\{a_1,a_2,...a_s\}A={a1,a2,...as},所有数都在[0,m−1][0,m-1][0,m− ...
- 【bzoj3684】 大朋友和多叉树 生成函数+多项式快速幂+拉格朗日反演
这题一看就觉得是生成函数的题... 我们不妨去推下此题的生成函数,设生成函数为$F(x)$,则$[x^s]F(x)$即为答案. 根据题意,我们得到 $F(x)=x+\sum_{i∈D} F^i(x)$ ...
- hdu2065"红色病毒"问题(指数母函数+快速幂取模)
"红色病毒"问题 Time Limit: 1000/1000 MS (Java/Others) Memory Limit: 32768/32768 K (Java/Other ...
随机推荐
- @KafkaListener和@KafkaListeners的使用
2. consumer 使用了@KafkaListener注解. 2.1. pom.xml 引入以下依赖 <dependency> <groupId>org.springfra ...
- 使用 pyenv 可以在一个系统中安装多个python版本
Installl related yum install readline readline-devel readline-static -y yum install openssl openssl- ...
- LeetCode 第 14 场双周赛
基础的 api 还是不够熟悉啊 5112. 十六进制魔术数字 class Solution { public: char *lltoa(long long num, char *str, int ra ...
- LeetCode 第 164 场周赛
访问所有点的最小时间 不难看出,从点(x1,y1) 到 (x2,y2) 的步数需要 min(dx,dy),其中 dx = abs(x1-x2),dy = abs(y1-y2) class Soluti ...
- (二)Spring中的ioc
目录 Spring的ioc操作 ioc底层使用的技术 ioc底层原理 ioc入门案例 bean管理(xml方式) IOC和DI的区别 Spring整合WEB的原理 Spring 整合的具体操作 Spr ...
- 【php设计模式】单例模式
实现单例的三个关键点: 1.使用一个静态成员来保持一个单例实例 2.一个私有的构造方法使得该类只能在类的内部方法中被实例化 3.在实例化对象的静态方法中,先判断静态变量是否已经被赋值,如果赋值则返回该 ...
- gitlab LFS 的应用实践
今天看到的gitlab LFS的文档,将自己的理解整理成博客,加深自己的印象.具体gitlab LFS的介绍可以直接百度了,不在这里详细阐述.只提一下他的作用:LFS就是Large File Stor ...
- 最简单的一个win32程序
#include <windows.h> HINSTANCE g_hInst = NULL; //2 窗口处理函数 LRESULT CALLBACK WndProc( HWND hWnd, ...
- spark2.0 DataSet操作的一些问题记录
随着新版本的Spark已经逐渐稳定,最近拟将原有框架升级到spark 2.0.还是比较兴奋的,特别是SQL的速度真的快了许多.. 然而,在其中一个操作时却卡住了.主要是dataframe.map操作, ...
- jquery.serializejson.min.js的妙用
关于这个jquery.serializejson.min.js插件来看,他是转json的一个非常简单好用的插件. 前端在处理含有大量数据提交的表单时,除了使用Form直接提交刷新页面之外,经常碰到的需 ...