算法习题---4-2正方形（UVa201）

一：题目

判断一个点阵中含有几个正方形（数正方形）

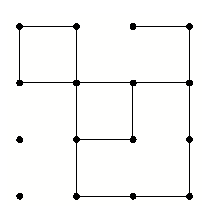
如图例中：有2个边长为1的正方形，1个边长为2的正方形

（一）题目详解

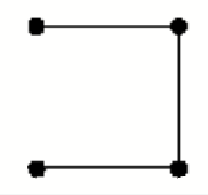
（二）样例输入

4　　　　　　 表示每行每列各有4个顶点
16　　  　　 表示整个点阵中共有16条边
H  1　　　　H表示水平边 从（1,1）->(1,2)之间有一条边　　注意：1 1 表示水平第一行第一个顶点
H
H
H
H
H
H
H
V  1　　　　V表示垂直边 从（1,1）->(2,1)之间有一条边 注意：1 1 表示垂直看第一列第一个顶点
V
V
V
V
V
V
V  

H
H
V  

二：代码实现

#define _CRT_SECURE_NO_WARNINGS
#include <stdio.h>
#include <stdlib.h>
#include <string.h>

#define N 9
int n,m;
int edge[N*N][];    //边信息
int square[N+][N+];    //正方形顶点信息,从（1，1）开始

获取边信息edge，并转换为一个二维数组square保存顶点信息《重点》

void getInfo()
{
    //获取顶点、边数
    scanf("%d", &n);
    scanf("%d", &m);

    //将边信息转换为正方形信息
    memset(square, sizeof(square), );

    //获取边信息
    for (int i = ; i < m; i++)
    {
        getchar();
        scanf("%c %d %d", (char*)&edge[i][], &edge[i][], &edge[i][]);
        //注意1表示水平有边，2表示垂直有边，既有水平，又有垂直为3
        //注意V的时候 V 2 1 是代表第二列第一个
        edge[i][] == 'H' ? square[edge[i][]][edge[i][]] +=  : square[edge[i][]][edge[i][]] += ;
    }
}

获取指定边数的正方形个数

int getNumForSq(int ec)
{
    //从正方形左上角开始从上到下,从左到右
    int num = ,x,y;
    for (int i = ; i <= n - ec;i++)    //列
    {
        for (int j = ; j <= n - ec;j++)    //行
        {
            if (square[j][i]!=)    //此处有顶点
            {
                //开始判断是否有指定大小正方形
                x = j, y = i;
                //判断上横边
                for (y = i; y <= i + ec-; y++)
                    if (!(square[x][y] ==  || square[x][y] == ))
                        goto Next;

                //判断下横边

                x = j + ec, y = i;
                for (y = i; y <= i + ec-; y++)
                    if (!(square[x][y] ==  || square[x][y] == ))
                        goto Next;

                //判断左边
                x = j, y = i;
                for (x = j; x <= j + ec-;x++)
                    if (!(square[x][y] ==  || square[x][y] == ))
                        goto Next;

                //判断右边
                x = j, y = i + ec;
                for (x = j; x <= j + ec-; x++)
                    if (!(square[x][y] ==  || square[x][y] == ))
                        goto Next;

                //构成正方形
                num++;
            }

        Next:;
        }
    }

    return num;
}

主函数

int main()
{
    FILE* fp=freopen("data2.in", "r", stdin);
    freopen("data2.out", "w", stdout);
    int i = , j,num,flag;

    while (!feof(fp))
    {
        //获取一组信息
        flag = ;
        getInfo();
        printf("Problem #%d\n\n", i++);

        //开始进行计算正方形大小 从1->n-1
        for (j = ; j < n;j++)
        {
            num = getNumForSq(j);
            if (num)
            {
                printf("%d square(s) of size %d\n", num, j);
                flag = ;
            }
        }

        flag ? printf("\n**************************\n\n") : printf("No completed squares can be found.\n");
    }

    freopen("CON", "r", stdin);
    freopen("CON", "w", stdout);

    return ;
}

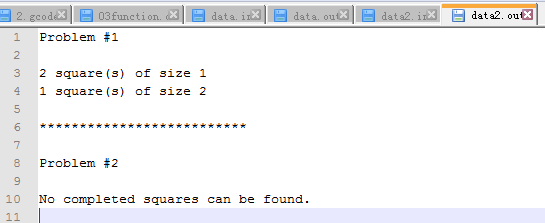
结果输出