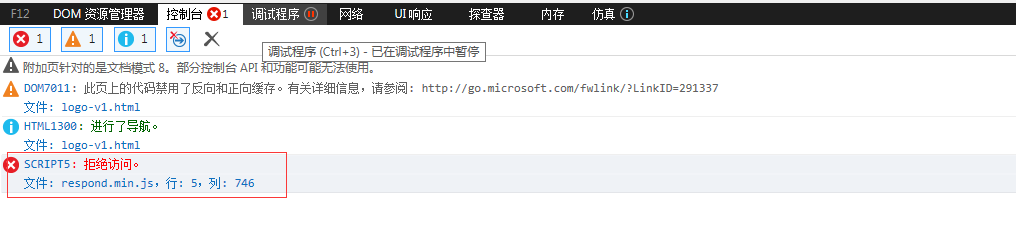
关于bootstrap的响应式插件respond.min.js在IE8下出现:拒绝访问。respond.min.js,行: 5,列: 746报错问题
本地在IE8浏览器下测试兼容性的时候,出现了以下的报错:
该问题在bootstrap的官网有介绍:https://v3.bootcss.com/getting-started

关于bootstrap的响应式插件respond.min.js在IE8下出现:拒绝访问。respond.min.js,行: 5,列: 746报错问题的更多相关文章
- 基于ASP.NET MVC和Bootstrap搭建响应式个人博客站(一)
1.0 为什么要做这个博客站? www.zynblog.com 在工作学习中,经常要搜索查找各种各样的资料,每次找到相关资料后都会顺手添加到浏览器书签中,时间一长,书签也就满了.而且下次再点击这个 ...
- Metronic – 超赞!基于 Bootstrap 的响应式后台管理模板
Metronic 是一套精美的响应式后台管理模板,基于强大的 Twitter Bootstrap 框架实现.Metronic 拥有简洁优雅的 Metro UI 风格界面,6 种颜色可选,76 个模板页 ...
- Django中间件,CSRF(跨站请求伪造),缓存,信号,BootStrap(模板)-响应式(栅格)+模板
Django中间件,CSRF(跨站请求伪造),缓存,信号,BootStrap(模板)-响应式(栅格)+模板 1.中间件(重要): 在Django的setting中有个MIDDLEWARE列表,里面的东 ...
- 响应式编程知多少 | Rx.NET 了解下
1. 引言 An API for asynchronous programming with observable streams. ReactiveX is a combination of the ...
- react native-调用react-native-fs插件时,如果数据的接口是需要验证信息的,在android上运行报错
调用react-native-fs插件时,如果数据的接口是需要验证信息的,在android上运行报错,而在iOS上运行没问题.原因是因为接口是有验证信息的,而调用这个插件时没有传入,在iOS上会自动加 ...
- 关于bootstrap和响应式布局
bootstrap导入 首先需要安装好插件 然后就是在代码器写导入代码 代码如下 <html lang="zh-CN"> <head> <meta c ...
- 基于 Bootstrap 的响应式后台管理面板
你想建立一个后台管理面板或者分析仪表板吗?不需从头开始,Keen IO Bootstrap 是一个响应式的仪表盘模板,可以帮助你在几分钟内呈现数据,让你可以创建一个有吸引力的,定制的分析仪表板,随时可 ...
- bootstrap固定响应式导航
<link rel="stylesheet" href="http://cdn.bootcss.com/bootstrap/3.2.0/css/bootstrap. ...
- Bootstrap之响应式导航栏
代码: <!DOCTYPE html> <html lang="zh"> <head> <meta charset="UTF-8 ...
随机推荐
- 题解 【Uva】硬币问题
[Uva]硬币问题 Description 有n种硬币,面值分别为v1, v2, ..., vn,每种都有无限多.给定非负整数S,可以选用多少个硬币,使得面值之和恰好为S?输出硬币数目的最小值和最大值 ...
- 011_linuxC++之_继承的引入
(一)面向对象程序设计中最重要的一个概念是继承.继承允许我们依据另一个类来定义一个类,这使得创建和维护一个应用程序变得更容易.这样做,也达到了重用代码功能和提高执行时间的效果. (二)引入继承程序 # ...
- jQuery系列(十四):jQuery中的ajax
1.什么是ajax AJAX = 异步的javascript和XML(Asynchronous Javascript and XML) 简言之,在不重载整个网页的情况下,AJAX通过后台加载数据,并在 ...
- Rapid Object Detection using a Boosted Cascade of Simple Features 部分翻译
Rapid ObjectDetection using a Boosted Cascade of Simple Features 使用简单特征级联分类器的快速目标检测 注:部分翻译不准处以红色字体给出 ...
- 前端导出pdf
html2canvas文档地址 http://html2canvas.hertzen.com/configuration 方式一:使用html2canvas和jspdf插件实现 该方式是通过html2 ...
- 最远 Manhattan 距离
最远 Manhattan 距离 处理问题 K维空间下的n个点,求两点最远曼哈顿距离 思路 以二维为例介绍算法思想,即可类推到k维.对于P,Q两点,曼哈顿距离|Px-Qx|+|Py-Qy|可看作(±Px ...
- jquery转换js
刚离职,一直忙于弄简历,整理面试题.今天得空吧前几天学习复习的jq基础知识整理一下,长时间不用还真的忘记了.所有在深入学习中也不要忘记复习之前的知识.做巩固,老话说的好打好根基才能盖好房.基础知识过后 ...
- python并发——进程间同步和通信
一.进程间同步 对于一些临界资源,不能使用并发无限消耗,就需要设置专门的临界标示,比如锁或者信号量等 from multiprocessing import Process, Lock import ...
- 网络编程udp入门
老师布置的作业 echo4_server.c #include<stdio.h> #include<stdlib.h> #include<string.h> #in ...
- 【转】Qt编写串口通信程序全程图文讲解
本文章原创于www.yafeilinux.com 转载请注明出处. (说明:我们的编程环境是windows xp下,在Qt Creator中进行,如果在Linux下或直接用源码编写,程序稍有不同,请自 ...
